
Calculus
10th Edition
ISBN: 9781285057095
Author: Ron Larson, Bruce H. Edwards
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Textbook Question
Chapter 11.5, Problem 102E
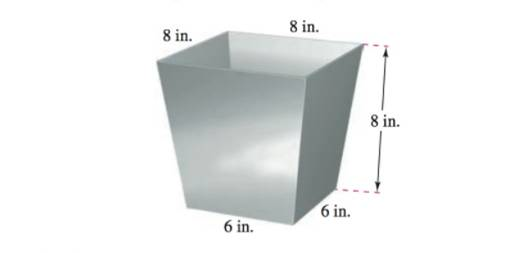
Mechanical Design The figure shows a chute at the top of a grain elevator of a combine that funnels the grain into a bin. Find the angle between two adjacent sides.
Expert Solution & Answer
Trending nowThis is a popular solution!
Learn your wayIncludes step-by-step video

schedule06:52
Chapter 11 Solutions
Calculus
Ch. 11.1 - CONCEPT CHECK Scalar and Vector Describe the...Ch. 11.1 - Sketching a Vector In Exercises 3 and 4, (a) find...Ch. 11.1 - Prob. 3ECh. 11.1 - Prob. 2ECh. 11.1 - Prob. 4ECh. 11.1 - Prob. 5ECh. 11.1 - Prob. 6ECh. 11.1 - Prob. 7ECh. 11.1 - Prob. 8ECh. 11.1 - Prob. 9E
Ch. 11.1 - Writing a Vector in Different Forms In Exercises...Ch. 11.1 - Prob. 11ECh. 11.1 - Prob. 12ECh. 11.1 - Prob. 13ECh. 11.1 - Prob. 14ECh. 11.1 - Prob. 15ECh. 11.1 - Prob. 16ECh. 11.1 - Sketching Scalar MultipliesIn Exercises 25 and 26,...Ch. 11.1 - Prob. 18ECh. 11.1 - Prob. 19ECh. 11.1 - Prob. 20ECh. 11.1 - Prob. 27ECh. 11.1 - Prob. 28ECh. 11.1 - Prob. 21ECh. 11.1 - Prob. 22ECh. 11.1 - Prob. 23ECh. 11.1 - Prob. 24ECh. 11.1 - Prob. 25ECh. 11.1 - Prob. 26ECh. 11.1 - Prob. 29ECh. 11.1 - Prob. 30ECh. 11.1 - Prob. 31ECh. 11.1 - Prob. 32ECh. 11.1 - Prob. 33ECh. 11.1 - Prob. 34ECh. 11.1 - Prob. 35ECh. 11.1 - Finding a Unit Vector In Exercises 35-38, find the...Ch. 11.1 - Prob. 37ECh. 11.1 - Prob. 38ECh. 11.1 - Finding MagnitudesIn Exercises 3942, find the...Ch. 11.1 - Finding Magnitudes In Exercises 39-42, find the...Ch. 11.1 - Prob. 41ECh. 11.1 - Prob. 42ECh. 11.1 - Prob. 43ECh. 11.1 - Prob. 44ECh. 11.1 - Prob. 45ECh. 11.1 - Prob. 46ECh. 11.1 - Prob. 47ECh. 11.1 - Prob. 48ECh. 11.1 - Prob. 49ECh. 11.1 - Prob. 50ECh. 11.1 - Prob. 51ECh. 11.1 - Prob. 52ECh. 11.1 - Finding a Vector In Exercises 53-56, find the...Ch. 11.1 - Prob. 54ECh. 11.1 - Prob. 55ECh. 11.1 - Prob. 56ECh. 11.1 - Prob. 58ECh. 11.1 - Prob. 59ECh. 11.1 - Prob. 60ECh. 11.1 - Prob. 61ECh. 11.1 - Prob. 62ECh. 11.1 - Prob. 63ECh. 11.1 - Prob. 64ECh. 11.1 - Prob. 65ECh. 11.1 - Prob. 66ECh. 11.1 - Prob. 67ECh. 11.1 - Prob. 68ECh. 11.1 - Prob. 69ECh. 11.1 - Prob. 70ECh. 11.1 - Finding Unit Vectors In Exercises 67-72, find a...Ch. 11.1 - Prob. 72ECh. 11.1 - Finding a Vector In Exercises 73 and 74, find the...Ch. 11.1 - Prob. 74ECh. 11.1 - Prob. 75ECh. 11.1 - Numerical and Graphical Analysis Forces with...Ch. 11.1 - Prob. 77ECh. 11.1 - Prob. 78ECh. 11.1 - Prob. 79ECh. 11.1 - Cable TensionIn Exercises 79 and 80, determine the...Ch. 11.1 - Projectile Motion A gun with a muzzle velocity of...Ch. 11.1 - Prob. 82ECh. 11.1 - Navigation A plane is flying with a bearing of...Ch. 11.1 - NavigationA plane flies at a constant groundspeed...Ch. 11.1 - Prob. 85ECh. 11.1 - Prob. 86ECh. 11.1 - Prob. 87ECh. 11.1 - Prob. 88ECh. 11.1 - Prob. 89ECh. 11.1 - Prob. 90ECh. 11.1 - Prob. 91ECh. 11.1 - Prob. 92ECh. 11.1 - Prob. 93ECh. 11.1 - Prob. 94ECh. 11.1 - Prob. 95ECh. 11.1 - Prob. 96ECh. 11.2 - CONCEPT CHECK Describing Coordinates A point in...Ch. 11.2 - Prob. 1ECh. 11.2 - Prob. 2ECh. 11.2 - Prob. 3ECh. 11.2 - Prob. 4ECh. 11.2 - Prob. 5ECh. 11.2 - Prob. 6ECh. 11.2 - Finding Coordinates of a PointIn Exercises 912,...Ch. 11.2 - Prob. 8ECh. 11.2 - Prob. 9ECh. 11.2 - Prob. 10ECh. 11.2 - Prob. 11ECh. 11.2 - Prob. 12ECh. 11.2 - Prob. 13ECh. 11.2 - Prob. 14ECh. 11.2 - Prob. 15ECh. 11.2 - Prob. 16ECh. 11.2 - Prob. 17ECh. 11.2 - Prob. 18ECh. 11.2 - Prob. 19ECh. 11.2 - Prob. 20ECh. 11.2 - Prob. 21ECh. 11.2 - Prob. 22ECh. 11.2 - Prob. 23ECh. 11.2 - Prob. 24ECh. 11.2 - Prob. 25ECh. 11.2 - Prob. 26ECh. 11.2 - Classifying a TriangleIn Exercises 2932, find the...Ch. 11.2 - Prob. 28ECh. 11.2 - Prob. 29ECh. 11.2 - Prob. 30ECh. 11.2 - Prob. 31ECh. 11.2 - Prob. 32ECh. 11.2 - Finding the Midpoint In Exercises 33-36, find the...Ch. 11.2 - Prob. 34ECh. 11.2 - Prob. 33ECh. 11.2 - Prob. 35ECh. 11.2 - Prob. 37ECh. 11.2 - Prob. 38ECh. 11.2 - Prob. 39ECh. 11.2 - Prob. 40ECh. 11.2 - Finding the Equation of a SphereIn Exercises 4346,...Ch. 11.2 - Finding the Equation of a SphereIn Exercises 4346,...Ch. 11.2 - Finding the Equation of a SphereIn Exercises 4346,...Ch. 11.2 - Finding the Equation of a Sphere In Exercises...Ch. 11.2 - Prob. 45ECh. 11.2 - Prob. 46ECh. 11.2 - Prob. 47ECh. 11.2 - Prob. 48ECh. 11.2 - Prob. 51ECh. 11.2 - Prob. 52ECh. 11.2 - Finding the Component Form of a Vector in SpaceIn...Ch. 11.2 - Prob. 53ECh. 11.2 - Prob. 54ECh. 11.2 - Prob. 55ECh. 11.2 - Prob. 56ECh. 11.2 - Prob. 57ECh. 11.2 - Prob. 58ECh. 11.2 - Prob. 59ECh. 11.2 - Prob. 60ECh. 11.2 - Prob. 61ECh. 11.2 - Prob. 62ECh. 11.2 - Prob. 63ECh. 11.2 - Prob. 64ECh. 11.2 - Prob. 65ECh. 11.2 - Prob. 66ECh. 11.2 - Prob. 67ECh. 11.2 - Prob. 68ECh. 11.2 - Prob. 69ECh. 11.2 - Prob. 70ECh. 11.2 - Prob. 71ECh. 11.2 - Prob. 72ECh. 11.2 - Prob. 73ECh. 11.2 - Prob. 74ECh. 11.2 - Prob. 75ECh. 11.2 - Prob. 76ECh. 11.2 - Prob. 77ECh. 11.2 - Prob. 78ECh. 11.2 - Prob. 79ECh. 11.2 - Prob. 80ECh. 11.2 - Prob. 81ECh. 11.2 - Prob. 82ECh. 11.2 - Prob. 83ECh. 11.2 - Prob. 84ECh. 11.2 - Prob. 85ECh. 11.2 - Prob. 86ECh. 11.2 - Prob. 87ECh. 11.2 - Sketching a Vector In Exercises 87 und 88, sketch...Ch. 11.2 - Prob. 89ECh. 11.2 - Prob. 90ECh. 11.2 - Prob. 92ECh. 11.2 - Prob. 91ECh. 11.2 - Prob. 94ECh. 11.2 - Prob. 95ECh. 11.2 - Prob. 96ECh. 11.2 - Prob. 97ECh. 11.2 - Prob. 98ECh. 11.2 - Prob. 99ECh. 11.2 - Prob. 100ECh. 11.2 - Auditorium Lights The lights in an auditorium are...Ch. 11.2 - Prob. 102ECh. 11.2 - Load Supports Find the tension in each of the...Ch. 11.2 - Prob. 104ECh. 11.2 - Prob. 105ECh. 11.3 - Finding Dot ProductsIn Exercises 310, find (a) uv...Ch. 11.3 - Prob. 2ECh. 11.3 - Prob. 3ECh. 11.3 - Prob. 4ECh. 11.3 - Prob. 5ECh. 11.3 - Prob. 6ECh. 11.3 - Prob. 7ECh. 11.3 - Prob. 8ECh. 11.3 - Prob. 9ECh. 11.3 - Finding the Angle Between Two Vectors In Exercises...Ch. 11.3 - Finding the Angle Between Two Vectors In Exercises...Ch. 11.3 - Prob. 12ECh. 11.3 - Finding the Angle Between Two Vectors In Exercises...Ch. 11.3 - Finding the Angle Between Two Vectors In Exercises...Ch. 11.3 - Prob. 15ECh. 11.3 - Prob. 16ECh. 11.3 - Prob. 17ECh. 11.3 - Prob. 18ECh. 11.3 - Comparing VectorsIn Exercises 2126, determine...Ch. 11.3 - Prob. 20ECh. 11.3 - Prob. 21ECh. 11.3 - Comparing VectorsIn Exercises 2126, determine...Ch. 11.3 - Comparing VectorsIn Exercises 2126, determine...Ch. 11.3 - Prob. 24ECh. 11.3 - Prob. 25ECh. 11.3 - Prob. 26ECh. 11.3 - Prob. 27ECh. 11.3 - Prob. 28ECh. 11.3 - Prob. 29ECh. 11.3 - Prob. 30ECh. 11.3 - Prob. 31ECh. 11.3 - Prob. 32ECh. 11.3 - Prob. 33ECh. 11.3 - Prob. 34ECh. 11.3 - Prob. 35ECh. 11.3 - Finding the Projection of u onto v In Exercises...Ch. 11.3 - Prob. 37ECh. 11.3 - Prob. 38ECh. 11.3 - Prob. 39ECh. 11.3 - Prob. 40ECh. 11.3 - Prob. 41ECh. 11.3 - Prob. 42ECh. 11.3 - Prob. 43ECh. 11.3 - Prob. 44ECh. 11.3 - Prob. 45ECh. 11.3 - Prob. 46ECh. 11.3 - Prob. 47ECh. 11.3 - Prob. 48ECh. 11.3 - Projection When the projection of u onto v has the...Ch. 11.3 - Prob. 50ECh. 11.3 - Revenue The vector u= 3240,1450,2235 gives the...Ch. 11.3 - RevenueRepeat Exercises 49 after decreasing the...Ch. 11.3 - Prob. 53ECh. 11.3 - Prob. 54ECh. 11.3 - Prob. 55ECh. 11.3 - Prob. 56ECh. 11.3 - Prob. 57ECh. 11.3 - Prob. 58ECh. 11.3 - Prob. 59ECh. 11.3 - Prob. 60ECh. 11.3 - Prob. 61ECh. 11.3 - Prob. 62ECh. 11.3 - Prob. 63ECh. 11.3 - Prob. 64ECh. 11.3 - Prob. 65ECh. 11.3 - Prob. 66ECh. 11.3 - Prob. 67ECh. 11.3 - Prob. 68ECh. 11.3 - Prob. 69ECh. 11.3 - Prob. 70ECh. 11.3 - Proof Use vectors to prove that the diagonals of a...Ch. 11.3 - Proof Use vectors to prove that a parallelogram is...Ch. 11.3 - Bond AngleConsider a regular tetrahedron with...Ch. 11.3 - Prob. 74ECh. 11.3 - Prob. 75ECh. 11.3 - Proof Prove the Cauchy-Schwarz Inequality, uv u v...Ch. 11.3 - Prob. 77ECh. 11.3 - Prob. 78ECh. 11.4 - Prob. 1ECh. 11.4 - Prob. 2ECh. 11.4 - Prob. 3ECh. 11.4 - Prob. 4ECh. 11.4 - Prob. 5ECh. 11.4 - Prob. 6ECh. 11.4 - Prob. 7ECh. 11.4 - Prob. 8ECh. 11.4 - Prob. 9ECh. 11.4 - Prob. 10ECh. 11.4 - Prob. 11ECh. 11.4 - Prob. 12ECh. 11.4 - Prob. 13ECh. 11.4 - Prob. 14ECh. 11.4 - Prob. 15ECh. 11.4 - Prob. 16ECh. 11.4 - Prob. 17ECh. 11.4 - Prob. 18ECh. 11.4 - Prob. 19ECh. 11.4 - Prob. 20ECh. 11.4 - Prob. 21ECh. 11.4 - Prob. 22ECh. 11.4 - Prob. 23ECh. 11.4 - Prob. 24ECh. 11.4 - Prob. 25ECh. 11.4 - Area In Exercises 23 and 24, verify that the...Ch. 11.4 - Prob. 27ECh. 11.4 - Prob. 28ECh. 11.4 - Torque The brakes on a bicycle are applied using a...Ch. 11.4 - Prob. 30ECh. 11.4 - Optimization A force of 180 pounds acts on the...Ch. 11.4 - Optimization A force of 56 pounds acts on the pipe...Ch. 11.4 - Prob. 33ECh. 11.4 - Prob. 34ECh. 11.4 - Prob. 35ECh. 11.4 - Prob. 36ECh. 11.4 - Volume In Exercises 35 and 36, use t triple scalar...Ch. 11.4 - Volume In Exercises 35 and 36, use t triple scalar...Ch. 11.4 - Volume In Exercises 37 and 38, find the volume of...Ch. 11.4 - Volume In Exercises 37 and 38, find the volume of...Ch. 11.4 - Prob. 41ECh. 11.4 - Prob. 42ECh. 11.4 - Prob. 43ECh. 11.4 - Prob. 44ECh. 11.4 - Prob. 45ECh. 11.4 - Prob. 46ECh. 11.4 - Prob. 47ECh. 11.4 - Prob. 48ECh. 11.4 - Prob. 49ECh. 11.4 - Prob. 50ECh. 11.4 - Prob. 51ECh. 11.4 - Prob. 52ECh. 11.4 - Prob. 53ECh. 11.4 - Prob. 54ECh. 11.4 - Proof In Exercises 47-52, prove the property of...Ch. 11.4 - Prob. 56ECh. 11.4 - Proof Prove that uv=uv if u and v are orthogonal.Ch. 11.4 - Prob. 58ECh. 11.4 - Prob. 59ECh. 11.5 - CONCEPT CHECK Parametric and Symmetric...Ch. 11.5 - Prob. 1ECh. 11.5 - Prob. 2ECh. 11.5 - Prob. 3ECh. 11.5 - Prob. 4ECh. 11.5 - Prob. 5ECh. 11.5 - Finding Parametric and Symmetric Equations In...Ch. 11.5 - Prob. 7ECh. 11.5 - Prob. 8ECh. 11.5 - Prob. 9ECh. 11.5 - Prob. 10ECh. 11.5 - Finding Parametric and Symmetric Equations In...Ch. 11.5 - Prob. 12ECh. 11.5 - Prob. 13ECh. 11.5 - Prob. 14ECh. 11.5 - Prob. 15ECh. 11.5 - Prob. 16ECh. 11.5 - Prob. 17ECh. 11.5 - Prob. 18ECh. 11.5 - Prob. 19ECh. 11.5 - Prob. 20ECh. 11.5 - Prob. 21ECh. 11.5 - Prob. 22ECh. 11.5 - Prob. 23ECh. 11.5 - Prob. 24ECh. 11.5 - Determining Parallel Lines In Exercises 29-32,...Ch. 11.5 - Prob. 26ECh. 11.5 - Prob. 27ECh. 11.5 - Determining Parallel Lines In Exercises 29-32,...Ch. 11.5 - Finding a Point of IntersectionIn Exercises 3336,...Ch. 11.5 - Prob. 30ECh. 11.5 - Prob. 31ECh. 11.5 - Prob. 32ECh. 11.5 - Prob. 33ECh. 11.5 - Prob. 34ECh. 11.5 - Prob. 35ECh. 11.5 - Finding an Equation of a PlaneIn Exercises 3944,...Ch. 11.5 - Finding an Equation of a PlaneIn Exercises 3944,...Ch. 11.5 - Prob. 38ECh. 11.5 - Prob. 39ECh. 11.5 - Finding an Equation of a PlaneIn Exercises 3944,...Ch. 11.5 - Finding an Equation of a PlaneIn Exercises 4556,...Ch. 11.5 - Finding an Equation of a PlaneIn Exercises 4556,...Ch. 11.5 - Finding an Equation of a PlaneIn Exercises 4556,...Ch. 11.5 - Finding an Equation of a PlaneIn Exercises 4556,...Ch. 11.5 - Finding an Equation of a PlaneIn Exercises 4556,...Ch. 11.5 - Finding an Equation of a PlaneIn Exercises 4556,...Ch. 11.5 - Finding an Equation of a PlaneIn Exercises 4556,...Ch. 11.5 - Finding an Equation of a PlaneIn Exercises 4556,...Ch. 11.5 - Finding an Equation of a PlaneIn Exercises 4556,...Ch. 11.5 - Finding an Equation of a PlaneIn Exercises 4556,...Ch. 11.5 - Finding an Equation of a PlaneIn Exercises 4556,...Ch. 11.5 - Finding an Equation of a PlaneIn Exercises 4556,...Ch. 11.5 - Finding an Equation of a PlaneIn Exercises 5760,...Ch. 11.5 - Prob. 54ECh. 11.5 - Prob. 55ECh. 11.5 - Prob. 56ECh. 11.5 - Prob. 71ECh. 11.5 - Prob. 72ECh. 11.5 - Parallel PlanesIn Exercises 6164, determine...Ch. 11.5 - Prob. 74ECh. 11.5 - Intersection of PlanesIn Exercises 6568, (a) find...Ch. 11.5 - Prob. 76ECh. 11.5 - Prob. 57ECh. 11.5 - Prob. 58ECh. 11.5 - Prob. 59ECh. 11.5 - Prob. 60ECh. 11.5 - Prob. 61ECh. 11.5 - Prob. 62ECh. 11.5 - Prob. 63ECh. 11.5 - Prob. 64ECh. 11.5 - Prob. 65ECh. 11.5 - Prob. 66ECh. 11.5 - Prob. 67ECh. 11.5 - Prob. 68ECh. 11.5 - Prob. 69ECh. 11.5 - Prob. 70ECh. 11.5 - Prob. 77ECh. 11.5 - Prob. 78ECh. 11.5 - Prob. 79ECh. 11.5 - Prob. 80ECh. 11.5 - Prob. 81ECh. 11.5 - Prob. 82ECh. 11.5 - Prob. 83ECh. 11.5 - Prob. 84ECh. 11.5 - Prob. 85ECh. 11.5 - Finding the Distance Between Two Parallel Planes...Ch. 11.5 - Prob. 87ECh. 11.5 - Prob. 88ECh. 11.5 - Prob. 89ECh. 11.5 - Prob. 90ECh. 11.5 - Prob. 91ECh. 11.5 - Prob. 92ECh. 11.5 - Prob. 93ECh. 11.5 - Prob. 94ECh. 11.5 - Prob. 96ECh. 11.5 - Prob. 97ECh. 11.5 - Prob. 98ECh. 11.5 - Prob. 99ECh. 11.5 - HOW DO YOU SEE IT? Match the general equation with...Ch. 11.5 - Prob. 101ECh. 11.5 - Mechanical Design The figure shows a chute at the...Ch. 11.5 - DistanceTwo insects are crawling along different...Ch. 11.5 - Prob. 104ECh. 11.5 - Finding a Point of IntersectionFind the point of...Ch. 11.5 - Prob. 106ECh. 11.5 - Finding a Point of Intersection Find the point of...Ch. 11.5 - Prob. 108ECh. 11.5 - Prob. 109ECh. 11.5 - True or False? In Exercises 113118, determine...Ch. 11.5 - Prob. 111ECh. 11.5 - Prob. 112ECh. 11.5 - Prob. 113ECh. 11.5 - Prob. 114ECh. 11.6 - Prob. 1ECh. 11.6 - Matching In Exercises 5-10, match the equation...Ch. 11.6 - Prob. 3ECh. 11.6 - Prob. 4ECh. 11.6 - Prob. 5ECh. 11.6 - Prob. 6ECh. 11.6 - Prob. 7ECh. 11.6 - Prob. 8ECh. 11.6 - Prob. 9ECh. 11.6 - Prob. 10ECh. 11.6 - Prob. 11ECh. 11.6 - Sketching a Surface in SpaceIn Exercises 1114,...Ch. 11.6 - Prob. 17ECh. 11.6 - Prob. 13ECh. 11.6 - Prob. 14ECh. 11.6 - Prob. 15ECh. 11.6 - Prob. 20ECh. 11.6 - Prob. 16ECh. 11.6 - Prob. 18ECh. 11.6 - Prob. 23ECh. 11.6 - Prob. 19ECh. 11.6 - Prob. 21ECh. 11.6 - Prob. 22ECh. 11.6 - Prob. 24ECh. 11.6 - Prob. 25ECh. 11.6 - Prob. 26ECh. 11.6 - Prob. 27ECh. 11.6 - Prob. 28ECh. 11.6 - Prob. 29ECh. 11.6 - Prob. 36ECh. 11.6 - Prob. 35ECh. 11.6 - Prob. 30ECh. 11.6 - Prob. 31ECh. 11.6 - Finding an Equation for a Surface of Revolution In...Ch. 11.6 - Finding an Equation for a Surface of Revolution In...Ch. 11.6 - Prob. 34ECh. 11.6 - Finding a Generating CurveIn Exercises 3740, find...Ch. 11.6 - Prob. 38ECh. 11.6 - Prob. 39ECh. 11.6 - Prob. 40ECh. 11.6 - Prob. 41ECh. 11.6 - Analyzing a TraceIn Exercises 43 and 44, analyze...Ch. 11.6 - Prob. 43ECh. 11.6 - Prob. 44ECh. 11.6 - Prob. 45ECh. 11.6 - Machine Design The top of a rubber bushing...Ch. 11.6 - Using a Hyperbolic ParaboloidDetermine the...Ch. 11.6 - Prob. 48ECh. 11.6 - Prob. 49ECh. 11.6 - True or False? In Exercises 49-52, determine...Ch. 11.6 - Prob. 51ECh. 11.6 - Prob. 52ECh. 11.6 - Prob. 53ECh. 11.7 - Cylindrical-to-Rectangular ConversionIn Exercises...Ch. 11.7 - Cylindrical-to-Rectangular ConversionIn Exercises...Ch. 11.7 - Prob. 3ECh. 11.7 - Prob. 4ECh. 11.7 - Cylindrical-to-Rectangular ConversionIn Exercises...Ch. 11.7 - Prob. 6ECh. 11.7 - Prob. 7ECh. 11.7 - Prob. 8ECh. 11.7 - Prob. 9ECh. 11.7 - Prob. 10ECh. 11.7 - Prob. 11ECh. 11.7 - Prob. 12ECh. 11.7 - Prob. 13ECh. 11.7 - Prob. 14ECh. 11.7 - Rectangular-to-Cylindrical Conversion In Exercises...Ch. 11.7 - Rectangular-to-Cylindrical Conversion In Exercises...Ch. 11.7 - Prob. 17ECh. 11.7 - Prob. 18ECh. 11.7 - Prob. 19ECh. 11.7 - Prob. 20ECh. 11.7 - Cylindrical-to-Rectangular ConversionIn Exercises...Ch. 11.7 - Prob. 22ECh. 11.7 - Prob. 23ECh. 11.7 - Prob. 24ECh. 11.7 - Prob. 25ECh. 11.7 - Prob. 26ECh. 11.7 - Prob. 27ECh. 11.7 - Prob. 28ECh. 11.7 - Prob. 29ECh. 11.7 - Rectangular-to-Spherical ConversionIn Exercises...Ch. 11.7 - Prob. 31ECh. 11.7 - Prob. 32ECh. 11.7 - Prob. 33ECh. 11.7 - Prob. 34ECh. 11.7 - Prob. 35ECh. 11.7 - Prob. 36ECh. 11.7 - Prob. 37ECh. 11.7 - Prob. 38ECh. 11.7 - Prob. 39ECh. 11.7 - Prob. 40ECh. 11.7 - Prob. 41ECh. 11.7 - Prob. 42ECh. 11.7 - Prob. 43ECh. 11.7 - Prob. 44ECh. 11.7 - Prob. 45ECh. 11.7 - Prob. 46ECh. 11.7 - Prob. 47ECh. 11.7 - Rectangular-to-Spherical ConversionIn Exercises...Ch. 11.7 - Prob. 49ECh. 11.7 - Prob. 50ECh. 11.7 - Prob. 51ECh. 11.7 - Prob. 52ECh. 11.7 - Prob. 53ECh. 11.7 - Prob. 54ECh. 11.7 - Prob. 55ECh. 11.7 - Prob. 56ECh. 11.7 - Prob. 63ECh. 11.7 - Prob. 64ECh. 11.7 - Prob. 68ECh. 11.7 - Prob. 69ECh. 11.7 - Prob. 70ECh. 11.7 - Prob. 71ECh. 11.7 - Prob. 72ECh. 11.7 - Prob. 75ECh. 11.7 - Prob. 76ECh. 11.7 - Prob. 77ECh. 11.7 - Prob. 78ECh. 11.7 - Prob. 57ECh. 11.7 - Prob. 58ECh. 11.7 - Prob. 59ECh. 11.7 - Prob. 60ECh. 11.7 - Prob. 61ECh. 11.7 - Prob. 62ECh. 11.7 - Spherical Coordinates Explain why in spherical...Ch. 11.7 - Prob. 82ECh. 11.7 - Prob. 65ECh. 11.7 - Prob. 66ECh. 11.7 - Prob. 67ECh. 11.7 - Prob. 73ECh. 11.7 - Prob. 74ECh. 11.7 - Prob. 79ECh. 11.7 - Prob. 81ECh. 11.7 - Prob. 83ECh. 11.7 - Prob. 84ECh. 11.7 - Prob. 85ECh. 11.7 - Prob. 86ECh. 11.7 - Prob. 87ECh. 11.7 - Prob. 88ECh. 11.7 - Prob. 89ECh. 11.7 - Prob. 90ECh. 11.7 - Prob. 91ECh. 11.7 - Prob. 92ECh. 11.7 - Prob. 93ECh. 11.7 - Prob. 94ECh. 11.7 - Prob. 95ECh. 11.7 - Sketching a Solid In Exercises 9194, sketch the...Ch. 11.7 - Prob. 97ECh. 11.7 - Prob. 98ECh. 11.7 - Prob. 99ECh. 11.7 - Prob. 100ECh. 11.7 - Prob. 101ECh. 11.7 - Prob. 102ECh. 11.7 - Prob. 103ECh. 11.7 - Prob. 104ECh. 11.7 - Prob. 105ECh. 11.7 - Prob. 106ECh. 11.7 - Prob. 107ECh. 11.7 - Prob. 108ECh. 11.7 - Intersection of SurfaceIdentify the curve of...Ch. 11.7 - Prob. 110ECh. 11 - Writing Vectors in Different Forms In Exercises 1...Ch. 11 - Prob. 2RECh. 11 - Prob. 3RECh. 11 - Prob. 4RECh. 11 - Prob. 5RECh. 11 - Prob. 6RECh. 11 - Prob. 7RECh. 11 - Prob. 8RECh. 11 - Prob. 9RECh. 11 - Prob. 10RECh. 11 - Prob. 11RECh. 11 - Prob. 12RECh. 11 - Prob. 13RECh. 11 - Prob. 14RECh. 11 - Prob. 15RECh. 11 - Prob. 16RECh. 11 - Prob. 17RECh. 11 - Prob. 18RECh. 11 - Prob. 19RECh. 11 - Prob. 20RECh. 11 - Prob. 21RECh. 11 - Prob. 22RECh. 11 - Prob. 23RECh. 11 - Prob. 24RECh. 11 - Prob. 25RECh. 11 - Prob. 26RECh. 11 - Prob. 27RECh. 11 - Prob. 28RECh. 11 - Prob. 29RECh. 11 - Prob. 30RECh. 11 - Prob. 31RECh. 11 - Prob. 32RECh. 11 - Prob. 33RECh. 11 - Prob. 34RECh. 11 - Prob. 35RECh. 11 - Prob. 36RECh. 11 - Finding a Unit VectorFind a unit vector that is...Ch. 11 - Prob. 38RECh. 11 - Prob. 39RECh. 11 - VolumeUse the triple scalar product to find the...Ch. 11 - Prob. 41RECh. 11 - Prob. 42RECh. 11 - Prob. 43RECh. 11 - Prob. 44RECh. 11 - Prob. 45RECh. 11 - Prob. 46RECh. 11 - Prob. 47RECh. 11 - Prob. 48RECh. 11 - Prob. 49RECh. 11 - Prob. 50RECh. 11 - Prob. 51RECh. 11 - Prob. 52RECh. 11 - Distance Find the distance between the planes...Ch. 11 - Prob. 54RECh. 11 - Prob. 55RECh. 11 - Prob. 56RECh. 11 - Prob. 57RECh. 11 - Prob. 58RECh. 11 - Prob. 59RECh. 11 - Prob. 60RECh. 11 - Prob. 61RECh. 11 - Prob. 62RECh. 11 - Prob. 63RECh. 11 - Prob. 64RECh. 11 - Prob. 65RECh. 11 - Prob. 66RECh. 11 - Prob. 67RECh. 11 - Prob. 68RECh. 11 - Prob. 69RECh. 11 - Prob. 70RECh. 11 - Prob. 71RECh. 11 - Prob. 72RECh. 11 - Prob. 73RECh. 11 - Prob. 74RECh. 11 - Prob. 75RECh. 11 - Prob. 76RECh. 11 - Prob. 77RECh. 11 - Prob. 78RECh. 11 - Prob. 1PSCh. 11 - Prob. 2PSCh. 11 - Prob. 3PSCh. 11 - Prob. 4PSCh. 11 - Prob. 5PSCh. 11 - Prob. 6PSCh. 11 - Volume (a) Find the volume of the solid bounded...Ch. 11 - Prob. 8PSCh. 11 - Prob. 9PSCh. 11 - Prob. 10PSCh. 11 - Sketching Graphs Sketch the graph of each equation...Ch. 11 - Prob. 12PSCh. 11 - Tetherball A tetherball weighing 1 pound is pulled...Ch. 11 - Towing A loaded barge is being towed by two...Ch. 11 - Prob. 15PSCh. 11 - Latitude-Longitude SystemLos Angeles is located at...Ch. 11 - Distance Between a Point and a PlaneConsider the...Ch. 11 - Prob. 18PSCh. 11 - Prob. 19PSCh. 11 - Prob. 20PS
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- Velocity Pitcher Aroldis Chapman threw a pitch with a recorded velocity of 105 miles per hour. Assuming he threw the pitch at an angle of 3.5 below the horizontal, find the vertical and horizontal components of the velocity. (Source: Guinness World Records)arrow_forwardTake this test as you would take a test in class. When you are finished, check your work against the answers given in the back of the book. A water sprinkler sprays water on a lawn over a distance of 25 feet and rotates through an angle of 130. Find the area of the lawn watered by the sprinkler.arrow_forwardAn amusement park ride the Octopus has eight support arms that are equally spaced about a circle. What is the measure of the central angle formed by two consecutive arms?arrow_forward
- Fill in the blanks. Two angles that have the same initial and terminal sides are ________.arrow_forwardObservation Wheel The High Roller, located on the Las Vegas Strip in Paradise. Nevada, is currently the largest observation wheel in the world with a diameter of 520 feet. The top of the wheel stands 550 feet above the ground. Find the height of a rider after the wheel has rotated through an angle of 110. Assume the rider boards at the bottom of the wheel.arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage LearningAlgebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage LearningAlgebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL Trigonometry (MindTap Course List)TrigonometryISBN:9781305652224Author:Charles P. McKeague, Mark D. TurnerPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781305652224Author:Charles P. McKeague, Mark D. TurnerPublisher:Cengage Learning Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,

Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781337278461
Author:Ron Larson
Publisher:Cengage Learning

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage

Holt Mcdougal Larson Pre-algebra: Student Edition...
Algebra
ISBN:9780547587776
Author:HOLT MCDOUGAL
Publisher:HOLT MCDOUGAL

Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781305652224
Author:Charles P. McKeague, Mark D. Turner
Publisher:Cengage Learning

Algebra and Trigonometry (MindTap Course List)
Algebra
ISBN:9781305071742
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:Cengage Learning

Elementary Geometry For College Students, 7e
Geometry
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Cengage,
The Law of Cosines; Author: Professor Dave Explains;https://www.youtube.com/watch?v=3wGQMyaWoLA;License: Standard YouTube License, CC-BY
Law of Sines and Law of Cosines (4 Examples); Author: Mario's Math Tutoring;https://www.youtube.com/watch?v=T--nPHdS1Vo;License: Standard YouTube License, CC-BY