Algebra & Trigonometry with Analytic Geometry
13th Edition
ISBN:9781133382119
Author:Swokowski
Publisher:Swokowski
Chapter1: Fundamental Concepts Of Algebra
Section1.3: Algebraic Expressions
Problem 44E
Related questions
Question
Finding a One-Sided Limit In Exercises find the one-sided limit (if it exists).
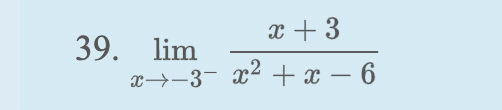
Transcribed Image Text:x + 3
39.
lim
x→-3- x² +x – 6
Expert Solution
Step 1
Trending now
This is a popular solution!
Step by step
Solved in 2 steps with 2 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Recommended textbooks for you

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage

College Algebra
Algebra
ISBN:
9781305115545
Author:
James Stewart, Lothar Redlin, Saleem Watson
Publisher:
Cengage Learning

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage

College Algebra
Algebra
ISBN:
9781305115545
Author:
James Stewart, Lothar Redlin, Saleem Watson
Publisher:
Cengage Learning
Expert Answers to Latest Homework Questions
Q: dont provide handwritinh solution ...
Q: Indicate whether (a) and (b) are radial nodes or nodal planes:
a
2s
(a) is a
(b) is a
>
<
b
2PX
Q: K
Save
A brine solution of salt flows at a constant rate of 8 L/min into a large tank that initially…
Q: dont provide handwriting solution...
Q: How much energy is required to change 10.0 g of H2O(s) initially at -30.0 °C into H2O(l) at 50.0 °C?…
Q: In sodium, one of the two yellow lines has a wavelength of 589.76 nm and is the transition from the…
Q: For the following reaction in the sequence, please give conditions that will best make
the desired…
Q: Which of the following solutions would make an effective buffer?
1. HCIO and NACIO
II. NaOH and NaBr…
Q: You are given the following cash flow information for Project A:
Project A PV Outflows
TV Inflows…
Q: (1 point)
Juan purchases an annuity for $3100 that will make 21 annual payments, the first to come…
Q: None
Q: None
Q: None
Q: A portable concrete test instrument used in construction for evaluating and profiling concrete…
Q: What is meant by monetary neutrality? How exactly does an increase in the money supply lead to a…
Q: Based off the calculated conventional benefit-cost ratios (BCRs) for both options (the…
Q: Referring to the graph below, complete the sentence by choosing the correct response from the…
Q: None
Q: None
Q: None
Q: EX: A 30 m diameter wind turbine is placed on a 50 m tower in terrain with a power law coefficient…