
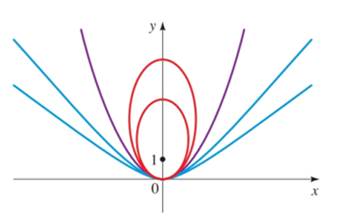
DISCUSS: A Family of Confocal Conics Conics that share a focus are called confocal. Consider the family of conics that have a focus at
(a) Find equations of two different ellipses that have these properties.
(b) Find equations of two different hyperbolas that have these properties.
(c) Explain why only one parabola satisfies these properties. Find it’s equation.
(d) Sketch the conics you found in parts (a),(b), and (c) on the same coordinate axes (for the hyperbolas, sketch top branches only).
(e) How are the ellipses and hyperbolas related to the parabola?
Trending nowThis is a popular solution!

Chapter 12 Solutions
Algebra and Trigonometry (MindTap Course List)
 Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning College AlgebraAlgebraISBN:9781305115545Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
College AlgebraAlgebraISBN:9781305115545Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning

