Textbook Problem

PROBLEM PLUS

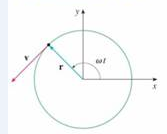
FIGURE FOR PROBLEM 1

1. A particle P moves with constant angular speed ω around a circle whose center is at the origin and whose radius is R. The particle is said to be in uniform circular motion. Assume that the motion is counterclockwise and that the panicle is at the point (R, 0) when t     = 0, The position vector at time t ≥ 0 is r(t) = R cos ωt i + R sin ωt j.

(a) Find the velocity vector v and show that v · r = 0, Conclude that v is tangent to the circle and points in the direction of the motion

(b) Show that the speed |v| of the particle is the constant ωR. The period T of the particle is the time required for one complete resolution. Conclude that $\text{T}\text{ = }\frac{2\text{π}\text{R}}{\left|\text{v}\right|}\text{ = }\frac{2\text{π}}{\omega }$

(c) Find the acceleration vector a. Show that it is proportional to r and that it points toward the origin. An acceleration with this property is called a centripetal acceleration. Show that the magnitude of the acceleration vector is |a| = Rω².

(d) Suppose that the particle has mass m. Show that the magnitude of the force F that is required to produce this, motion, called a centripetal force. is $\left|\text{F}\right|\text{ = }\frac{\text{m}|\text{v}{|}^2}{\text{R}}$