Interference of sound
Seiche
A seiche is an oscillating standing wave in a body of water. The term seiche pronounced saysh) can be understood by the sloshing of water back and forth in a swimming pool. The same phenomenon happens on a much larger scale in vast bodies of water including bays and lakes. A seizure can happen in any enclosed or semi-enclosed body of water.
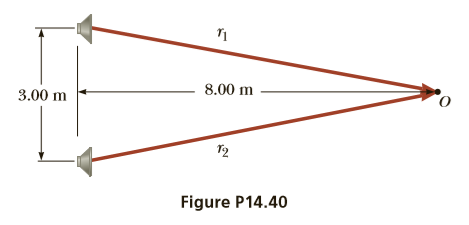
Two loudspeakers are placed above and below each other, as in Figure P14.40 and driven by the same source at a frequency of 4.50 x 102 Hz. An observer is in front of the speakers (to the right) at point O, at the same distance from each speaker. What minimum vertical distance upward should the top speaker be moved to create destructive interference at point O?
Trending now
This is a popular solution!
Step by step
Solved in 3 steps with 3 images




