Math
CalculusMultivariable CalculusUse the level curves in the figure to predict the location of the critical points of f and whether f has a saddle point or a local maximum or minimum at each critical point. Explain your reasoning. Then use the Second Derivatives Test to confirm your predictions. 4. f (x, y) = 3 x − x 3 − 2 y 2 +3 y 4

Use the level curves in the figure to predict the location of the critical points of f and whether f has a saddle point or a local maximum or minimum at each critical point. Explain your reasoning. Then use the Second Derivatives Test to confirm your predictions. 4. f (x, y) = 3 x − x 3 − 2 y 2 +3 y 4

BuyFind

Multivariable Calculus

8th Edition
James Stewart
Publisher: Cengage Learning
ISBN: 9781305266643
BuyFind

Multivariable Calculus

8th Edition
James Stewart
Publisher: Cengage Learning
ISBN: 9781305266643

Solutions

Chapter
Section
Problem 1E
Problem 2E
Problem 3E
Problem 4E
Problem 5E
Problem 6E
Problem 7E
Problem 8E
Problem 9E
Problem 10E
Problem 11E
Problem 12E
Problem 13E
Problem 14E
Problem 15E
Problem 16E
Problem 17E
Problem 18E
Problem 19E
Problem 20E
Problem 21E
Problem 22E
Problem 23E
Problem 24E
Problem 25E
Problem 26E
Problem 27E
Problem 28E
Problem 29E
Problem 30E
Problem 31E
Problem 32E
Problem 33E
Problem 34E
Problem 35E
Problem 36E
Problem 37E
Problem 38E
Problem 39E
Problem 40E
Problem 41E
Problem 42E
Problem 43E
Problem 44E
Problem 45E
Problem 46E
Problem 47E
Problem 48E
Problem 49E
Problem 50E
Problem 51E
Problem 52E
Problem 53E
Problem 54E
Problem 55E
Problem 56E
Problem 57E
Problem 58E
Problem 59E
Problem 60E
Chapter 14.7, Problem 4E
Textbook Problem

Use the level curves in the figure to predict the location of the critical points of f and whether f has a saddle point or a local maximum or minimum at each critical point. Explain your reasoning. Then use the Second Derivatives Test to confirm your predictions.

4. f(x, y) = 3x − x3 − 2y2 +3 y4

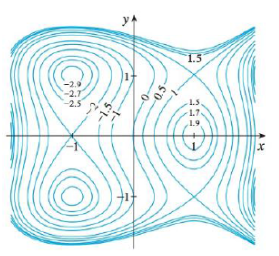
Chapter 14.7, Problem 4E, Use the level curves in the figure to predict the location of the critical points of f and whether f

Expert Solution

Want to see the full answer?

Check out a sample textbook solution.
Chapter 14.7,
Problem 3E
Chapter 14.7,
Problem 5E

Want to see this answer and more?

Experts are waiting 24/7 to provide step-by-step solutions in as fast as 30 minutes!*

*Response times vary by subject and question complexity. Median response time is 34 minutes and may be longer for new subjects.

Chapter 14 Solutions

Multivariable Calculus
Ch. 14.1 - In Example 2 we considered the function W = f(T,...Ch. 14.1 - The temperature-humidity index I (or humidex, for...Ch. 14.1 - A manufacturer has modeled its yearly production...Ch. 14.1 - Verify for the Cobb-Douglas production function...Ch. 14.1 - A model for the surface area of a human body is...Ch. 14.1 - The wind-chill index W discussed in Example 2 has...Ch. 14.1 - The wave heights h in the open sea depend on the...Ch. 14.1 - A company makes three sizes of cardboard boxes:...Ch. 14.1 - Let g(x, y) = cos(x + 2y). (a) Evaluate g(2, 1)....Ch. 14.1 - Let F(x,y)=1+4y2. (a) Evaluate F(3,1). (b) Find...
Ch. 14.1 - Let f(x,y,z)=x+y+z+ln(4x2y2z2). (a) Evaluate f(1,...Ch. 14.1 - Let g(x,y,z)=x3y2z10xyz. (a) Evaluate g(1, 2, 3)....Ch. 14.1 - Find and sketch the domain of the function. 13....Ch. 14.1 - Find and sketch the domain of the function. 14....Ch. 14.1 - Find and sketch the domain of the function. 15....Ch. 14.1 - Find and sketch the domain of the function....Ch. 14.1 - Find and sketch the domain of the function. 17....Ch. 14.1 - Find and sketch the domain of the function. 18....Ch. 14.1 - Find and sketch the domain of the function. 19....Ch. 14.1 - Find and sketch the domain of the function. 20....Ch. 14.1 - Find and sketch the domain of the function. 21....Ch. 14.1 - Find and sketch the domain of the function. 22....Ch. 14.1 - Sketch the graph of the function. 23. f(x, y) = yCh. 14.1 - Sketch the graph of the function. 24. f(x, y) = x2Ch. 14.1 - Sketch the graph of the function. 25. f(x, y) = 10...Ch. 14.1 - Sketch the graph of the function. 26. f(x, y) =...Ch. 14.1 - Sketch the graph of the function. 27. f(x, y) =...Ch. 14.1 - Sketch the graph of the function. 28. f(x, y) = 2 ...Ch. 14.1 - Sketch the graph of the function. 29. f(x, y) = x2...Ch. 14.1 - Sketch the graph of the function. 30....Ch. 14.1 - Sketch the graph of the function. 31....Ch. 14.1 - Match the function with its graph (labeled IVI)....Ch. 14.1 - A contour map for a function f is shown. Use it to...Ch. 14.1 - Shown is a contour map of atmospheric pressure in...Ch. 14.1 - Level curves (isothermals) are shown for the...Ch. 14.1 - Two contour maps are shown. One is for a function...Ch. 14.1 - Locate the points A and B on the map of Lonesome...Ch. 14.1 - Make a rough sketch of a contour map for the...Ch. 14.1 - The body mass index (BMI) of a person is defined...Ch. 14.1 - The body mass index is defined in Exercise 39....Ch. 14.1 - A contour map of a function is shown. Use it to...Ch. 14.1 - A contour map of a function is shown. Use it to...Ch. 14.1 - A contour map of a function is shown. Use it to...Ch. 14.1 - A contour map of a function is shown. Use it to...Ch. 14.1 - Draw a contour map of the function showing several...Ch. 14.1 - Draw a contour map of the function showing several...Ch. 14.1 - Draw a contour map of the function showing several...Ch. 14.1 - Draw a contour map of the function showing several...Ch. 14.1 - Draw a contour map of the function showing several...Ch. 14.1 - Draw a contour map of the function showing several...Ch. 14.1 - Draw a contour map of the function showing several...Ch. 14.1 - Draw a contour map of the function showing several...Ch. 14.1 - Sketch both a contour map and a graph of the...Ch. 14.1 - Sketch both a contour map and a graph of the...Ch. 14.1 - A thin metal plate, located in the xy-plane, has...Ch. 14.1 - If V(x, y) is the electric potential at a point...Ch. 14.1 - Use a computer to graph the function using various...Ch. 14.1 - Use a computer to graph the function using various...Ch. 14.1 - Use a computer to graph the function using various...Ch. 14.1 - Use a computer to graph the function using various...Ch. 14.1 - Match the function (a) with its graph (labeled AF...Ch. 14.1 - Match the function (a) with its graph (labeled AF...Ch. 14.1 - Match the function (a) with its graph (labeled AF...Ch. 14.1 - Match the function (a) with its graph (labeled AF...Ch. 14.1 - Match the function (a) with its graph (labeled AF...Ch. 14.1 - Match the function (a) with its graph (labeled AF...Ch. 14.1 - Describe the level surfaces of the function. 67....Ch. 14.1 - Describe the level surfaces of the function. 68....Ch. 14.1 - Describe the level surfaces of the function. 69....Ch. 14.1 - Describe the level surfaces of the function. 70....Ch. 14.1 - Describe how the graph of g is obtained from the...Ch. 14.1 - Describe how the graph of g is obtained from the...Ch. 14.1 - Use a computer to graph the function using various...Ch. 14.1 - Use a computer to graph the function using various...Ch. 14.1 - Graph the function using various domains and...Ch. 14.1 - Graph the function using various domains and...Ch. 14.1 - Investigate the family of functions...Ch. 14.1 - Use a computer to investigate the family of...Ch. 14.1 - Use a computer to investigate the family of...Ch. 14.1 - Graph the functions f(x,y)=x2+y2 f(x,y)=ex2+y2...Ch. 14.1 - (a) Show that, by taking logarithms, the general...Ch. 14.2 - Suppose that lim(x, y) (3, 1) = 6. What can you...Ch. 14.2 - Explain why each function is continuous or...Ch. 14.2 - Use a table of numerical values of f(x, y) for (x,...Ch. 14.2 - Use a table of numerical values of f(x, y) for (x,...Ch. 14.2 - Find the limit, if it exists, or show that the...Ch. 14.2 - Find the limit, if it exists, or show that the...Ch. 14.2 - Find the limit if it exists, or show that the...Ch. 14.2 - Find the limit if it exists, or show that the...Ch. 14.2 - Find the limit if it exists, or show that the...Ch. 14.2 - Find the limit if it exists, or show that the...Ch. 14.2 - Find the limit if it exists, or show that the...Ch. 14.2 - Find the limit if it exists, or show that the...Ch. 14.2 - Find the limit if it exists, or show that the...Ch. 14.2 - Find the limit if it exists, or show that the...Ch. 14.2 - Find the limit if it exists, or show that the...Ch. 14.2 - Find the limit if it exists, or show that the...Ch. 14.2 - Find the limit if it exists, or show that the...Ch. 14.2 - Find the limit if it exists, or show that the...Ch. 14.2 - Find the limit if it exists, or show that the...Ch. 14.2 - Find the limit if it exists, or show that the...Ch. 14.2 - Find the limit if it exists, or show that the...Ch. 14.2 - Find the limit if it exists, or show that the...Ch. 14.2 - U se a computer graph of the function to explain...Ch. 14.2 - U se a computer graph of the function to explain...Ch. 14.2 - Find h(x, y) = g(f(x, y)) and the set of points at...Ch. 14.2 - Find h(x, y) = g(f(x, y)) and the set of points at...Ch. 14.2 - Graph the function and observe where it is...Ch. 14.2 - Graph the function and observe where it is...Ch. 14.2 - Determine the set of points at which the function...Ch. 14.2 - Determine the set of points at which the function...Ch. 14.2 - Determine the set of points at which the function...Ch. 14.2 - Determine the set of points at which the function...Ch. 14.2 - Determine the set of points at which the function...Ch. 14.2 - Determine the set of points at which the function...Ch. 14.2 - Determine the set of points at which the function...Ch. 14.2 - Determine the set of points at which the function...Ch. 14.2 - Determine the set of points at which the function...Ch. 14.2 - Determine the set of points at which the function...Ch. 14.2 - Use polar coordinates to find the limit, [If (r, )...Ch. 14.2 - Use polar coordinates to find the limit, [If (r, )...Ch. 14.2 - Use polar coordinates to find the limit, [If (r, )...Ch. 14.2 - At the beginning of this section we considered the...Ch. 14.2 - Graph and discuss the continuity of the function...Ch. 14.2 - Let f(x,y)={0ify0oryx41if0yx4 (a) Show that f(x,...Ch. 14.2 - Show that the function f given by f(x) = |x| is...Ch. 14.2 - If c Vn, show that the function f given by f(x) =...Ch. 14.3 - The temperature T (in C) at a location in the...Ch. 14.3 - At the beginning of this section we discussed the...Ch. 14.3 - The wind-chill index W in die perceived...Ch. 14.3 - The wave heights h in the open sea depend on the...Ch. 14.3 - Determine the signs of the partial derivatives for...Ch. 14.3 - Determine the signs of the partial derivatives for...Ch. 14.3 - Determine the signs of the partial derivatives for...Ch. 14.3 - Determine the signs of the partial derivatives for...Ch. 14.3 - The following surfaces, labeled a, b, and c, are...Ch. 14.3 - A contour map is given for a function f. Use it to...Ch. 14.3 - If f(x, y) = 16 4x2 y2, find fx(1, 2) and fy(1,...Ch. 14.3 - If f(x,y)=4x24y2, find fx(1,0) and fy(1, 0) and...Ch. 14.3 - Find fx and fy and graph f, fx, and fy with...Ch. 14.3 - Find fx and fy and graph f, fx, and fy with...Ch. 14.3 - Find the first partial derivatives of the...Ch. 14.3 - Find the first partial derivatives of the...Ch. 14.3 - Find the first partial derivatives of the...Ch. 14.3 - Find the first partial derivatives of the...Ch. 14.3 - Find the first partial derivatives of the...Ch. 14.3 - Find the first partial derivatives of the...Ch. 14.3 - Find the first partial derivatives of the...Ch. 14.3 - Find the first partial derivatives of the...Ch. 14.3 - Find the first partial derivatives of the...Ch. 14.3 - Find the first partial derivatives of the...Ch. 14.3 - Find the first partial derivatives of the...Ch. 14.3 - Find the first partial derivatives of the...Ch. 14.3 - Find the first partial derivatives of the...Ch. 14.3 - Find the first partial derivatives of the...Ch. 14.3 - Find the first partial derivatives of the...Ch. 14.3 - Find the first partial derivatives of the...Ch. 14.3 - Find the first partial derivatives of the...Ch. 14.3 - Find the first partial derivatives of the...Ch. 14.3 - Find the first partial derivatives of the...Ch. 14.3 - Find the first partial derivatives of the...Ch. 14.3 - Find the first partial derivatives of the...Ch. 14.3 - Find the first partial derivatives of the...Ch. 14.3 - Find the first partial derivatives of the...Ch. 14.3 - Find the first partial derivatives of the...Ch. 14.3 - Find the first partial derivatives of the...Ch. 14.3 - Find the first partial derivatives of the...Ch. 14.3 - Find the indicated partial derivative. 41. R(s, t)...Ch. 14.3 - Find the indicated partial derivative. 42....Ch. 14.3 - Find the indicated partial derivative. 43....Ch. 14.3 - Find the indicated partial derivative. 44. f(x, y,...Ch. 14.3 - Use the definition of partial derivatives as...Ch. 14.3 - Use the definition of partial derivatives as...Ch. 14.3 - Use implicit differentiation to find z/x and z/y....Ch. 14.3 - Use implicit differentiation to find z/x and z/y....Ch. 14.3 - Use implicit differentiation to find z/x and z/y....Ch. 14.3 - Use implicit differentiation to find z/x and z/y....Ch. 14.3 - Find z/x and z/y. 51. (a) z = f(x) + g(y) (b) z =...Ch. 14.3 - Find z/x and z/y. 52. (a) z = f(x)g(y) (b) z =...Ch. 14.3 - Find all the second partial derivatives. 53. f(x,...Ch. 14.3 - Find all the second partial derivatives. 54. f(x,...Ch. 14.3 - Find all the second partial derivatives. 55....Ch. 14.3 - Find all the second partial derivatives. 56. T =...Ch. 14.3 - Find all the second partial derivatives. 57. v =...Ch. 14.3 - Find all the second partial derivatives. 58....Ch. 14.3 - Verify that the conclusion of Clairauts Theorem...Ch. 14.3 - Verify that the conclusion of Clairauts Theorem...Ch. 14.3 - Verify that the conclusion of Clairauts Theorem...Ch. 14.3 - Verify that the conclusion of Clairauts Theorem...Ch. 14.3 - Find the indicated partial derivative(s). 63. f(x,...Ch. 14.3 - Find the indicated partial derivative(s). 64. f(x,...Ch. 14.3 - Find the indicated partial derivative(s). 65....Ch. 14.3 - Find the indicated partial derivative(s). 66. g(r,...Ch. 14.3 - Find the indicated partial derivative(s). 67....Ch. 14.3 - Find the indicated partial derivative(s). 68. V =...Ch. 14.3 - Find the indicated partial derivative(s). 69....Ch. 14.3 - Find the indicated partial derivative(s). 70. u =...Ch. 14.3 - If f(x,y,z)=xy2z3+arcsin(xz), find fxzy. [Hint:...Ch. 14.3 - If g(x,y,z)=1+xz+1xy, find gxyz. [Hint: Which...Ch. 14.3 - Use the table of values of f(x, y) to estimate the...Ch. 14.3 - Level curves are shown for a function f. Determine...Ch. 14.3 - Verify that the function u=e2k2tsinkx is a...Ch. 14.3 - Determine whether each of the following functions...Ch. 14.3 - Verify that the function u=1/x2+y2+z2 is a...Ch. 14.3 - Show that each of the following functions is a...Ch. 14.3 - If f and g are twice differentiable functions of a...Ch. 14.3 - If u=ea1x1+a2x2++anxn, where a12+a22++an2=1, show...Ch. 14.3 - The diffusion equation ct=D2cx2 where D is a...Ch. 14.3 - The temperature at a point (x, y) on a flat metal...Ch. 14.3 - The total resistance R produced by three...Ch. 14.3 - Show that the Cobb-Douglas production function P =...Ch. 14.3 - Show that the Cobb-Douglas production function...Ch. 14.3 - Cobb and Douglas used the equation P(L, K) =...Ch. 14.3 - The van der Waals equation for n moles of a gas is...Ch. 14.3 - The gas law for a fixed mass m of an ideal gas at...Ch. 14.3 - For the ideal gas of Exercise 88, show that...Ch. 14.3 - The wind-chill index is modeled by the function W...Ch. 14.3 - A model for the surface area of a human body is...Ch. 14.3 - One of Poiseuilles laws states that the resistance...Ch. 14.3 - In the project on page 344 we expressed the power...Ch. 14.3 - The average energy E (in kcal) needed for a lizard...Ch. 14.3 - The kinetic energy of a body with mass m and...Ch. 14.3 - If a, b, c are the sides of a triangle and A, B, C...Ch. 14.3 - You are told that there is a function f whose...Ch. 14.3 - The paraboloid z = 6 x x22y2 intersects the...Ch. 14.3 - The ellipsoid 4x2 + 2y2 + z2 = 16 intersects the...Ch. 14.3 - In a study of frost penetration it was found that...Ch. 14.3 - Use Clairauts Theorem to show that if the...Ch. 14.3 - (a) How many nth-order partial derivatives does a...Ch. 14.3 - If f(x,y)=x(x2+y2)3/2esin(x2y) find fx(1,0)....Ch. 14.3 - If f(x,y)=x3+y33 find fx(0, 0).Ch. 14.4 - Find an equation of the tangent plane to the given...Ch. 14.4 - Find an equation of the tangent plane to the given...Ch. 14.4 - Find an equation of the tangent plane to the given...Ch. 14.4 - Find an equation of the tangent plane to the given...Ch. 14.4 - Find an equation of the tangent plane to the given...Ch. 14.4 - Find an equation of the tangent plane to the given...Ch. 14.4 - Graph the surface and the tangent plane at the...Ch. 14.4 - Graph the surface and the tangent plane at the...Ch. 14.4 - Explain why the function is differentiable at the...Ch. 14.4 - Explain why the function is differentiable at the...Ch. 14.4 - Explain why the function is differentiable at the...Ch. 14.4 - Explain why the function is differentiable at the...Ch. 14.4 - Explain why the function is differentiable at the...Ch. 14.4 - Explain why the function is differentiable at the...Ch. 14.4 - Verify the linear approximation at (0, 0). 17. ex...Ch. 14.4 - Verify the linear approximation at (0, 0). 18....Ch. 14.4 - Given that f is a differentiable function with...Ch. 14.4 - Find the linear approximation of the function f(x,...Ch. 14.4 - Find the linear approximation of the function...Ch. 14.4 - The wave heights h in the open sea depend on the...Ch. 14.4 - Use the table in Example 3 to find a linear...Ch. 14.4 - The wind-chill index W is the perceived...Ch. 14.4 - Find the differential of the function. 25. z = e2x...Ch. 14.4 - Find the differential of the function. 26....Ch. 14.4 - Find the differential of the function. 27. m =...Ch. 14.4 - Find the differential of the function. 28....Ch. 14.4 - Find the differential of the function. 29. R = 2...Ch. 14.4 - Find the differential of the function. 30....Ch. 14.4 - If z = 5x2 + y2 and (x, y) changes from (1, 2) to...Ch. 14.4 - If z = x2 xy + 3y2 and (x, y) changes from (3, 1)...Ch. 14.4 - The length and width of a rectangle are measured...Ch. 14.4 - Use differentials to estimate the amount of metal...Ch. 14.4 - Use differentials to estimate the amount of tin in...Ch. 14.4 - The wind-chill index is modeled by the function W...Ch. 14.4 - The tension T in the string of the yo-yo in the...Ch. 14.4 - The pressure, volume, and temperature of a mole of...Ch. 14.4 - If R is the total resistance of three resistors,...Ch. 14.4 - A model for the surface area of a human body is...Ch. 14.4 - In Exercise 14.1.39 and Example 14.3.3, the body...Ch. 14.4 - Suppose you need to know an equation of the...Ch. 14.4 - Show that the function is differentiable by...Ch. 14.4 - Show that the function is differentiable by...Ch. 14.4 - Prove that if f is a function of two variables...Ch. 14.4 - (a) The function...Ch. 14.5 - Use the Chain Rule to find dz/dt or dw/dt. 1. z =...Ch. 14.5 - Use the Chain Rule to find dz/dt or dw/dt. 2....Ch. 14.5 - Use the Chain Rule to find dz/dt or dw/dt. 3. z =...Ch. 14.5 - Use the Chain Rule to find dz/dt or dw/dt. 4....Ch. 14.5 - Use the Chain Rule to find dz/dt or dw/dt. 5. w =...Ch. 14.5 - Use the Chain Rule to find dz/dt or dw/dt. 6. w =...Ch. 14.5 - Use the Chain Rule to find z/s and z/t. 7. z = (x ...Ch. 14.5 - Use the Chain Rule to find z/s and z/t. 8. z =...Ch. 14.5 - Use the Chain Rule to find z/s and z/t. 9. z =...Ch. 14.5 - Use the Chain Rule to find z/s and z/t. 10. z =...Ch. 14.5 - Use the Chain Rule to find z/s and z/t. 11. z = er...Ch. 14.5 - Use the Chain Rule to find z/s and z/t. 12. z =...Ch. 14.5 - Let p(t) = f(x,y), where f is differentiable, x =...Ch. 14.5 - Let R(s, t) = G(u(s, t), v(s, t)), where G, u, and...Ch. 14.5 - Suppose f is a differentiable function of x and y,...Ch. 14.5 - Suppose f is a differentiable function of x and y,...Ch. 14.5 - Use a tree diagram to write out the Chain Rule for...Ch. 14.5 - Use a tree diagram to write out the Chain Rule for...Ch. 14.5 - Use a tree diagram to write out the Chain Rule for...Ch. 14.5 - Use a tree diagram to write out the Chain Rule for...Ch. 14.5 - Use the Chain Rule to find the indicated partial...Ch. 14.5 - Use the Chain Rule to find the indicated partial...Ch. 14.5 - Use the Chain Rule to find the indicated partial...Ch. 14.5 - Use the Chain Rule to find the indicated partial...Ch. 14.5 - Use the Chain Rule to find the indicated partial...Ch. 14.5 - Use the Chain Rule to find the indicated partial...Ch. 14.5 - Use Equation 6 to find dy/dx. 27. y cos x = x2 +...Ch. 14.5 - Use Equation 6 to find dy/dx. 28. cos(xy) = 1 +...Ch. 14.5 - Use Equation 6 to find dy/dx. 29. tan1(x2y) = x +...Ch. 14.5 - Use Equation 6 to find dy/dx. 30. ey sin x = x +...Ch. 14.5 - Use Equations 7 to find z/x and z/y. 31. x2 + 2y2...Ch. 14.5 - Use Equations 7 to find z/x and z/y. 32. x2 y2 +...Ch. 14.5 - Use Equations 7 to find z/x and z/y. 33. ez = xyzCh. 14.5 - Use Equations 7 to find z/x and z/y. 34. yz + x ln...Ch. 14.5 - The temperature at a point (x, y) is T(x, y),...Ch. 14.5 - Wheat production W in a given year depends on the...Ch. 14.5 - The speed of sound traveling through ocean water...Ch. 14.5 - The radius of a right circular cone is increasing...Ch. 14.5 - The length , width w, and height h of a box change...Ch. 14.5 - The voltage V in a simple electrical circuit is...Ch. 14.5 - The pressure of 1 mole of an ideal gas is...Ch. 14.5 - A manufacturer has modeled its yearly production...Ch. 14.5 - One side of a triangle is increasing at a rate of...Ch. 14.5 - A sound with frequency fs, is produced by a source...Ch. 14.5 - Assume that all the given functions are...Ch. 14.5 - Assume that all the given functions are...Ch. 14.5 - Assume that all the given functions are...Ch. 14.5 - Assume that all the given functions are...Ch. 14.5 - Assume that all the given functions have...Ch. 14.5 - Assume that all the given functions have...Ch. 14.5 - Assume that all the given functions have...Ch. 14.5 - Assume that all the given functions have...Ch. 14.5 - A function f is called homogeneous of degree n if...Ch. 14.5 - If f is homogeneous of degree n, show that...Ch. 14.5 - If f is homogeneous of degree n, show that fx(tx,...Ch. 14.5 - Suppose that the equation F(x, y, z) = 0...Ch. 14.5 - Equation 6 is a formula for the derivative dy/dx...Ch. 14.6 - Level curves for barometric pressure (in...Ch. 14.6 - The contour map shows the average maximum...Ch. 14.6 - A table of values for the wind-chill index W =...Ch. 14.6 - Find the directional derivative of f at the given...Ch. 14.6 - Find the directional derivative of f at the given...Ch. 14.6 - Find the directional derivative of f at the given...Ch. 14.6 - (a) Find the gradient of f. (b) Evaluate the...Ch. 14.6 - (a) Find the gradient of f. (b) Evaluate the...Ch. 14.6 - (a) Find the gradient of f. (b) Evaluate the...Ch. 14.6 - (a) Find the gradient of f. (b) Evaluate the...Ch. 14.6 - Find the directional derivative of the function at...Ch. 14.6 - Find the directional derivative of the function at...Ch. 14.6 - Find the directional derivative of the function at...Ch. 14.6 - Find the directional derivative of the function at...Ch. 14.6 - Find the directional derivative of the function at...Ch. 14.6 - Find the directional derivative of the function at...Ch. 14.6 - Find the directional derivative of the function at...Ch. 14.6 - Use the figure to estimate Du, f(2, 2).Ch. 14.6 - Find the directional derivative of f(x, y) = xy at...Ch. 14.6 - Find the directional derivative of f(x, y, z) =...Ch. 14.6 - Find the maximum rate of change of f at the given...Ch. 14.6 - Find the maximum rate of change of f at the given...Ch. 14.6 - Find the maximum rate of change of f at the given...Ch. 14.6 - Find the maximum rate of change of f at the given...Ch. 14.6 - Find the maximum rate of change of f at the given...Ch. 14.6 - Find the maximum rate of change of f at the given...Ch. 14.6 - (a) Show that a differentiable function f...Ch. 14.6 - Find the directions in which the directional...Ch. 14.6 - Find all points at which the direction of fastest...Ch. 14.6 - Near a buoy, the depth of a lake at the point with...Ch. 14.6 - The temperature T in a metal ball is inversely...Ch. 14.6 - The temperature at a point (x, y, z) is given by...Ch. 14.6 - Suppose that over a certain region of space the...Ch. 14.6 - Suppose you are climbing a hill whose shape is...Ch. 14.6 - Let f be a function of two variables that has...Ch. 14.6 - Shown is a topographic map of Blue River Pine...Ch. 14.6 - Show that the operation of taking the gradient of...Ch. 14.6 - Sketch the gradient vector f(4. 6) for the...Ch. 14.6 - The second directional derivative of f(x, y) is...Ch. 14.6 - (a) If u = a, b is a unit vector and f has...Ch. 14.6 - Find equations of (a) the tangent plane and (b)...Ch. 14.6 - Find equations of (a) the tangent plane and (b)...Ch. 14.6 - Find equations of (a) the tangent plane and (b)...Ch. 14.6 - Find equations of (a) the tangent plane and (b)...Ch. 14.6 - Find equations of (a) the tangent plane and (b)...Ch. 14.6 - Find equations of (a) the tangent plane and (b)...Ch. 14.6 - Use a computer to graph the surface, the tangent...Ch. 14.6 - Use a computer to graph the surface, the tangent...Ch. 14.6 - If f(x, y) = xy, find the gradient vector f(3, 2)...Ch. 14.6 - If g(x, y) = x2 + y2 4x, find the gradient vector...Ch. 14.6 - Show that the equation of the tangent plane to the...Ch. 14.6 - Find the equation of the tangent plane to the...Ch. 14.6 - Show that the equation of the tangent plane to the...Ch. 14.6 - At what point on the ellipsoid x2 + y2 + 2z2 = 1...Ch. 14.6 - Are there any points on the hyperboloid x2 y2 z2...Ch. 14.6 - Show that the ellipsoid 3x2 + 2y2 + z2 = 9 and the...Ch. 14.6 - Show that every plane that is tangent to the cone...Ch. 14.6 - Show that every normal line to the sphere x2 + y2...Ch. 14.6 - Where does the normal line to the paraboloid z =...Ch. 14.6 - At what points does the normal line through the...Ch. 14.6 - Show that the sum of the x-, y-, and z-intercepts...Ch. 14.6 - Show that the pyramids cut off from the first...Ch. 14.6 - Find parametric equations tor the tangent line to...Ch. 14.6 - (a) The plane y + z = 3 intersects the cylinder x2...Ch. 14.6 - Where does the helix r(t) = cos t, sin t, t...Ch. 14.6 - The helix r(t) = cos(t/2), sin(t/2), t) intersects...Ch. 14.6 - (a) Two surfaces are called orthogonal at a point...Ch. 14.6 - (a) Show that the function f(x, y) = xy3 is...Ch. 14.6 - Suppose that the directional derivatives of f(x,...Ch. 14.6 - Show that if z = f(x, y) is differentiable at x0 =...Ch. 14.7 - Suppose (1, 1) is a critical point of a function f...Ch. 14.7 - Suppose (0, 2) is a critical point of a function y...Ch. 14.7 - Use the level curves in the figure to predict the...Ch. 14.7 - Use the level curves in the figure to predict the...Ch. 14.7 - Find the local maximum and minimum values and...Ch. 14.7 - Find the local maximum and minimum values and...Ch. 14.7 - Find the local maximum and minimum values and...Ch. 14.7 - Find the local maximum and minimum values and...Ch. 14.7 - Find the local maximum and minimum values and...Ch. 14.7 - Find the local maximum and minimum values and...Ch. 14.7 - Find the local maximum and minimum values and...Ch. 14.7 - Find the local maximum and minimum values and...Ch. 14.7 - Find the local maximum and minimum values and...Ch. 14.7 - Find the local maximum and minimum values and...Ch. 14.7 - Find the local maximum and minimum values and...Ch. 14.7 - Find the local maximum and minimum values and...Ch. 14.7 - Find the local maximum and minimum values and...Ch. 14.7 - Find the local maximum and minimum values and...Ch. 14.7 - Find the local maximum and minimum values and...Ch. 14.7 - Find the local maximum and minimum values and...Ch. 14.7 - Show that f(x, y) = x2 + 4y2 4xy + 2 has an...Ch. 14.7 - Show that f(x,y)=x2yex2y2 has maximum values at...Ch. 14.7 - Use a graph or level curves or both to estimate...Ch. 14.7 - Use a graph or level curves or both to estimate...Ch. 14.7 - Use a graph or level curves or both to estimate...Ch. 14.7 - Use a graph or level curves or both to estimate...Ch. 14.7 - Use a graphing device as in Example 4 (or Newtons...Ch. 14.7 - Use a graphing device as in Example 4 (or Newtons...Ch. 14.7 - Use a graphing device as in Example 4 (or Newtons...Ch. 14.7 - Use a graphing device as in Example 4 (or Newtons...Ch. 14.7 - Find the absolute maximum and minimum values of f...Ch. 14.7 - Find the absolute maximum and minimum values of f...Ch. 14.7 - Find the absolute maximum and minimum values of f...Ch. 14.7 - Find the absolute maximum and minimum values of f...Ch. 14.7 - Find the absolute maximum and minimum values of f...Ch. 14.7 - Find the absolute maximum and minimum values of f...Ch. 14.7 - Find the absolute maximum and minimum values of f...Ch. 14.7 - Find the absolute maximum and minimum values of f...Ch. 14.7 - For functions of one variable it is impossible for...Ch. 14.7 - If a function of one variable is continuous on an...Ch. 14.7 - Find the shortest distance from the |point (2, 0,...Ch. 14.7 - Find the point on the plane x 2y + 3z = 6 that is...Ch. 14.7 - Find the points on the cone z2 = x2 + y2 that are...Ch. 14.7 - Find the points on the surface y2 = 9 + xz that...Ch. 14.7 - Find three positive numbers whose sum is 100 and...Ch. 14.7 - Find three positive numbers whose sum is 12 and...Ch. 14.7 - Find the maximum volume of a rectangular box that...Ch. 14.7 - Find the dimensions of the box with volume 1000...Ch. 14.7 - Find the volume of the largest rectangular box in...Ch. 14.7 - Find the dimensions of the rectangular box with...Ch. 14.7 - Find the dimensions of a rectangular box of...Ch. 14.7 - The base of an aquarium with given volume V is...Ch. 14.7 - A cardboard box without a lid is to have a volume...Ch. 14.7 - A rectangular building is being designed to...Ch. 14.7 - If the length of the diagonal of a rectangular box...Ch. 14.7 - A model for the yield Y of an agricultural crop as...Ch. 14.7 - The Shannon index (sometimes called the...Ch. 14.7 - Three alleles (alternative versions of a gene) A,...Ch. 14.7 - Suppose that a scientist has reason to believe...Ch. 14.7 - Find an equation of the plane that passes through...Ch. 14.8 - Pictured are a contour map of f and a curve with...Ch. 14.8 - (a) Use a graphing calculator or computer to graph...Ch. 14.8 - Each of these extreme value problems has a...Ch. 14.8 - Each of these extreme value problems has a...Ch. 14.8 - Each of these extreme value problems has a...Ch. 14.8 - Each of these extreme value problems has a...Ch. 14.8 - Each of these extreme value problems has a...Ch. 14.8 - Each of these extreme value problems has a...Ch. 14.8 - Each of these extreme value problems has a...Ch. 14.8 - Each of these extreme value problems has a...Ch. 14.8 - Each of these extreme value problems has a...Ch. 14.8 - Each of these extreme value problems has a...Ch. 14.8 - Each of these extreme value problems has a...Ch. 14.8 - Each of these extreme value problems has a...Ch. 14.8 - The method of Lagrange multipliers assumes that...Ch. 14.8 - Find the minimum value of f(x, y, z) = x2 + 2y2 +...Ch. 14.8 - Find the extreme values of f subject to both...Ch. 14.8 - Find the extreme values of f subject to both...Ch. 14.8 - Find the extreme values of f subject to both...Ch. 14.8 - Find the extreme values of f subject to both...Ch. 14.8 - Find the extreme values of f on the region...Ch. 14.8 - Find the extreme values of f on the region...Ch. 14.8 - Find the extreme values of f on the region...Ch. 14.8 - Consider the problem of maximizing the function...Ch. 14.8 - Consider the problem of minimizing the function...Ch. 14.8 - The total production P of a certain product...Ch. 14.8 - Referring to Exercise 27, we now suppose that the...Ch. 14.8 - Use Lagrange multipliers to prove that the...Ch. 14.8 - Use Lagrange multipliers to prove that the...Ch. 14.8 - Use Lagrange multipliers to give an alternate...Ch. 14.8 - Use Lagrange multipliers to give an alternate...Ch. 14.8 - Use Lagrange multipliers to give an alternate...Ch. 14.8 - Use Lagrange multipliers to give an alternate...Ch. 14.8 - Use Lagrange multipliers to give an alternate...Ch. 14.8 - Use Lagrange multipliers to give an alternate...Ch. 14.8 - Use Lagrange multipliers to give an alternate...Ch. 14.8 - Use Lagrange multipliers to give an alternate...Ch. 14.8 - Use Lagrange multipliers to give an alternate...Ch. 14.8 - Use Lagrange multipliers to give an alternate...Ch. 14.8 - Use Lagrange multipliers to give an alternate...Ch. 14.8 - Use Lagrange multipliers to give an alternate...Ch. 14.8 - Use Lagrange multipliers to give an alternate...Ch. 14.8 - Find the maximum and minimum volumes of a...Ch. 14.8 - The plane x + y + 2z = 2 intersects the paraboloid...Ch. 14.8 - The plane 4x 3y + 8z = 5 intersects the cone z2 =...Ch. 14.8 - (a) Find the maximum value of...Ch. 14.8 - (a) Maximize i=1nxiyi subject to the constraints...Ch. 14 - (a) What is a function of two variables? (b)...Ch. 14 - What is a function of three variables? How can you...Ch. 14 - What does lim(x,y)(a,b)f(x,y)=L mean? How can you...Ch. 14 - (a) What does it mean to say that f is continuous...Ch. 14 - (a) Write expressions for the partial derivatives...Ch. 14 - What does Clairauts Theorem say?Ch. 14 - How do you find a tangent plane to each of the...Ch. 14 - Define the linearization of f at (a, b). What is...Ch. 14 - (a) What does it mean to say that f is...Ch. 14 - If z = f(x, y), what arc the differentials dx, dy,...Ch. 14 - State the Chain Rule for the case where z = f(x,...Ch. 14 - If z is defined implicitly as a function of x and...Ch. 14 - (a) Write an expression as a limit for the...Ch. 14 - (a) Define the gradient vector f for a function f...Ch. 14 - What do the following statements mean? (a) f has a...Ch. 14 - (a) If f has a local maximum at (a, b), what can...Ch. 14 - State the Second Derivatives Test.Ch. 14 - (a) What is a closed set in 2? What is a bounded...Ch. 14 - Explain how the method of Lagrange multipliers...Ch. 14 - Determine whether the statement is true or false....Ch. 14 - Determine whether the statement is true or false....Ch. 14 - Determine whether the statement is true or false....Ch. 14 - Determine whether the statement is true or false....Ch. 14 - Determine whether the statement is true or false....Ch. 14 - Determine whether the statement is true or false....Ch. 14 - Determine whether the statement is true or false....Ch. 14 - Determine whether the statement is true or false....Ch. 14 - Determine whether the statement is true or false....Ch. 14 - Determine whether the statement is true or false....Ch. 14 - Determine whether the statement is true or false....Ch. 14 - Determine whether the statement is true or false....Ch. 14 - Find and sketch the domain of the function. 1....Ch. 14 - Find and sketch the domain of the function. 2....Ch. 14 - Sketch the graph of the function. 3. f(x, y) = 1 ...Ch. 14 - Sketch the graph of the function. 4. f(x, y) = x2...Ch. 14 - Sketch several level curves of the function. 5....Ch. 14 - Sketch several level curves of the function. 6....Ch. 14 - Make a rough sketch of a contour map for the...Ch. 14 - The contour map of a function f is shown, (a)...Ch. 14 - Evaluate the limit or show that it does not exist....Ch. 14 - Evaluate the limit or show that it does not exist....Ch. 14 - A metal plate is situated in the xy-plane and...Ch. 14 - Find a linear approximation to the temperature...Ch. 14 - Find the first partial derivatives. 13. f(x, y) =...Ch. 14 - Find the first partial derivatives. 14....Ch. 14 - Find the first partial derivatives. 15. F(, ) = 2...Ch. 14 - Find the first partial derivatives. 16. G(x, y, z)...Ch. 14 - Find the first partial derivatives. 17....Ch. 14 - The speed of sound traveling through ocean water...Ch. 14 - Find all second partial derivatives of f. 19. f(x,...Ch. 14 - Find all second partial derivatives of f. 20. z =...Ch. 14 - Find all second partial derivatives of f. 21. f(x,...Ch. 14 - Find all second partial derivatives of f. 22. v =...Ch. 14 - If z = xy + xey/x show that xzx+yzy=xy+z.Ch. 14 - If z = sin(x + sin t), show that zx2zxt=zt2zx2Ch. 14 - Find equations of (a) the tangent plane and (b)...Ch. 14 - Find equations of (a) the tangent plane and (b)...Ch. 14 - Find equations of (a) the tangent plane and (b)...Ch. 14 - Find equations of (a) the tangent plane and (b)...Ch. 14 - Find equations of (a) the tangent plane and (b)...Ch. 14 - Use a computer to graph the surface z = x2 + y4...Ch. 14 - Find the points on the hyperboloid x2 + 4y2 z2 =...Ch. 14 - Find du if u = ln(1 + se2t).Ch. 14 - Find the linear approximation of the function...Ch. 14 - The two legs of a right triangle are measured as 5...Ch. 14 - If u = x2y3 + z4, where x = p + 3p2, y = pep, and...Ch. 14 - If v = x2sin y + yexy, where x = s + 2t and y =...Ch. 14 - Suppose z = f(x, y), where x = g(s, t), y = h(s,...Ch. 14 - Use a tree diagram to write out the Chain Rule for...Ch. 14 - If z = y + f(x2 y2), where f is differentiable,...Ch. 14 - The length x of a side of a triangle is increasing...Ch. 14 - If z =f(u, v), where u = xy, v = y/x, and f has...Ch. 14 - If cos(xyz) = 1 + .x2y2 + z2, find zx and zy.Ch. 14 - Find the gradient of the function f(x,y,z)=x2eyz2.Ch. 14 - (a) When is the directional derivative of f a...Ch. 14 - Find the directional derivative of f at the given...Ch. 14 - Find the directional derivative of f at the given...Ch. 14 - Find the maximum rate of change of f(x,y)=x2y+y at...Ch. 14 - Find the direction in which f(x, y, z) =...Ch. 14 - The contour map shows wind speed in knots during...Ch. 14 - Find parametric equations of the tangent line at...Ch. 14 - Find the local maximum and minimum values and...Ch. 14 - Find the local maximum and minimum values and...Ch. 14 - Find the local maximum and minimum values and...Ch. 14 - Find the local maximum and minimum values and...Ch. 14 - Find the absolute maximum and minimum values of f...Ch. 14 - Find the absolute maximum and minimum values of f...Ch. 14 - Use a graph or level curves or both to estimate...Ch. 14 - Use a graphing calculator or computer (or Newtons...Ch. 14 - Use Lagrange multipliers to find the maximum and...Ch. 14 - Use Lagrange multipliers to find the maximum and...Ch. 14 - Use Lagrange multipliers to find the maximum and...Ch. 14 - Use Lagrange multipliers to find the maximum and...Ch. 14 - Find the points on the surface xy2z3= 2 that are...Ch. 14 - A package in the shape of a rectangular box can be...Ch. 14 - A pentagon is formed by placing an isosceles...Ch. 14 - A rectangle with length L and width W is cut into...Ch. 14 - Marine biologists have determined that when a...Ch. 14 - A long piece of galvanized sheet metal with width...Ch. 14 - For what values of the number r is the function...Ch. 14 - Suppose f is a differentiable function of one...Ch. 14 - (a) Newton's method for approximating a root of an...Ch. 14 - If the ellipse x2/a2 + y2/b2 = 1 is to enclose the...Ch. 14 - Show that the maximum value of the function...

Additional Math Textbook Solutions

Find more solutions based on key concepts
Linear Equations The given equation is either linear or equivalent to a linear equation. Solve the equation. 26...

Precalculus: Mathematics for Calculus (Standalone Book)

Convert each expression in Exercises 25-50 into its technology formula equivalent as in the table in the text. ...

Finite Mathematics and Applied Calculus (MindTap Course List)

True or False? In Exercises 69-72, determine whether the statement is true or false. If it is false, explain wh...

Calculus: An Applied Approach (MindTap Course List)

Find the numbers b such that the average value of f(x) = 2 + 6x 3x2 on the interval [0, b] is equal to 3.

Single Variable Calculus: Early Transcendentals, Volume I

Calculate each expression in Exercises 124, giving the answer as a whole number or a fraction in lowest terms. ...

Applied Calculus

Finding a Limit In Exercises 11-28, find the limit. limx2xx2+1

Calculus: Early Transcendental Functions

Use Theorem 10 to find the curvature. 21. r(t) = t3 j + t2 k

Calculus: Early Transcendentals

Guguen and Jacob (2012) asked waitresses to wear different colored T-shirts on different days for a six-week pe...

Essentials of Statistics for The Behavioral Sciences (MindTap Course List)

SOC The following table lists the approximate number of cars per 1000 population for 15 nations. Compute the me...

Essentials Of Statistics

a Use implicit differentiation to find y if b Plot the curve in part a. What do you see? Prove that what you se...

Calculus (MindTap Course List)

WW3. Statistical methods are classified into two categories: descriptive and inferential. Describe the general ...

Statistics for The Behavioral Sciences (MindTap Course List)

Statistical Literacy Marcie conducted a study of the cost of breakfast cereal. She recorded the costs of severa...

Understanding Basic Statistics

U.S. GDP The gross domestic product (GDP) of the United States, in trillions of dollars, from 2011 through 2015...

Applied Calculus for the Managerial, Life, and Social Sciences: A Brief Approach

Draw, by hand, a rough sketch of the graph of each function. (a) y = sin x (b) y = cos x (c) y = tan x (d) y = ...

Single Variable Calculus

For customers purchasing a refrigerator at a certain appliance store, let A be the event that the refrigerator ...

Probability and Statistics for Engineering and the Sciences

Solve the equations in Exercises 126. 10x(x2+1)4(x3+1)510x2(x2+1)5(x3+1)4=0

Finite Mathematics

For Problems 5-54, perform the following operations with real numbers. Objectives 3-6 23(16)

Intermediate Algebra

Use the given nth-term formula to compute the first five terms of the sequence. an=2n3n2

Mathematical Excursions (MindTap Course List)

17. The Barclays own a home that was recently appraised for $219,000. The balance on their existing first mortg...

Contemporary Mathematics for Business & Consumers

Evaluate without using a calculator. tan1(tan30)

Trigonometry (MindTap Course List)

Let :312 be defined by ([x]3)=4[x]12 using the same notational convention as in Exercise 9. Prove that is a ri...

Elements Of Modern Algebra

In Exercise 9 to 16, use a calculator to find the indicated cosine ratio to four decimal places. cos0

Elementary Geometry For College Students, 7e

In Problems 41-44, determine whether the following pairs of equations represent parallel lines, perpendicular l...

Mathematical Applications for the Management, Life, and Social Sciences

Find the total resistance in the series circuit in Illustration 2. ILLUSTRATION 2

Elementary Technical Mathematics

CONCEPT CHECK Sums What is the value of n? (a) i=1ni=5(5+1)2 (b) i=1ni2=20(20+1)[2(20)+1]6

Calculus of a Single Variable

Finding a Limit In Exercises 3742. find a formula for the sum of n terms. Use the formula to find the limit as ...

Calculus: Early Transcendental Functions (MindTap Course List)

Find an equation for the conic that satisfies the given conditions. 36. Parabola, vertical axis, passing throug...

Single Variable Calculus: Early Transcendentals

TRAFFIC A traffic survey of the speed of the vehicles travelling along a stretch of Hampton Road between 4 P.M ...

Finite Mathematics for the Managerial, Life, and Social Sciences

Precalculus or Calculus In Exercises 3-6.decide whether the problem can be solved using precalculus or whether ...

Calculus

The length of a = 4i – j – 2k is: 11 21

Study Guide for Stewart's Multivariable Calculus, 8th

Given the Taylor Series , a Taylor series for ex/2 is:

Study Guide for Stewart's Single Variable Calculus: Early Transcendentals, 8th

A study of pregnant grey seals resulted in n = 25 observations on the variables y = Fetus progesterone level (m...

Introduction To Statistics And Data Analysis

In Exercises 1 to 4, state the ratio needed, and use it to find the measure of the indicated line segment to th...

Elementary Geometry for College Students

Using the Fundamental Theorem of Line Integrals In Exercises 918, evaluate cF.dr Using the Fundamental Theorem ...

Multivariable Calculus

Volume In Exercises 15-20, use cylindrical coordinates to find the volume of the solid. Solid bounded above by ...

Calculus (MindTap Course List)

Describe the three techniques used to quantify behavioral observations and the three techniques used for sampli...

Research Methods for the Behavioral Sciences (MindTap Course List)

The following problems are given in decimal (standard) form. Calculate and give answers in scientific notation....

Mathematics For Machine Technology

Find c such that each of the following is true. a. p(0<z<c)=0.3686 b. p(c<z<0)=0.4706 c. p(c<z<c)=0.2510 d. p(z...

Mathematics: A Practical Odyssey

What is the goal of a single-case experimental research design?

Research Methods for the Behavioral Sciences (MindTap Course List)

Consider the following hypothesis test. H0: = 20 Ha: 20 The population standard deviation is 10. Use = .05....

STATISTICS F/BUSINESS+ECONOMICS-TEXT

Use a calculator to help solve each problem. Population growth The growth of a towns population is modeled by P...

College Algebra (MindTap Course List)

Given that z is a standard normal random variable, compute the following probabilities. a. P(z 1.0) b. P(z 1)...

Statistics for Business & Economics, Revised (MindTap Course List)

Restaurant Satisfaction. The Consumer Reports Restaurant Customer Satisfaction Survey is based upon 148,599 vis...

Essentials Of Statistics For Business & Economics

For the following exercises, use composition to determine which pairs of functions are inverses. 201. f(x)=5x7,...

Calculus Volume 1

Reminder Round all answers to two decimal places unless otherwise indicated. The Population of Canada In 2011 t...

Functions and Change: A Modeling Approach to College Algebra (MindTap Course List)

73. The days to maturity for a sample of five money market funds are shown here. The dollar amounts invested in...

Modern Business Statistics with Microsoft Office Excel (with XLSTAT Education Edition Printed Access Card) (MindTap Course List)

Answer Problems 110 without referring back to the text. Fill in the blanks or answer true or false. 4. If the s...

A First Course in Differential Equations with Modeling Applications (MindTap Course List)

Use truth tables to show that the argument forms are valid. Indicate which columns represent the premises and w...

Discrete Mathematics With Applications

Fill in the blanks. Two algebraic expressions that have the same domain and yield the same values for all numbe...

College Algebra

Use the following information to answer the next flue exercises: Javier volunteers in community events each mon...

Introductory Statistics

Find the derivative. 456. ddx1x34t2dt

Calculus Volume 2

bartleby
  • Contact Research (Essays)
  • High School Textbooks
  • Literature Guides
  • Essay Help
  • Mobile App
    • © 2021 bartleby. All Rights Reserved.