
Concept explainers
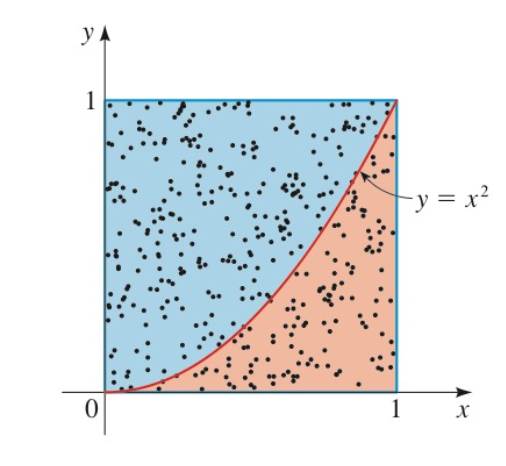
Areas of Curved Regions The Monte Carlo method can be used to estimate the area under the graph of a function. The figure below shows the region under the graph of
Modify the program from Problem

Want to see the full answer?
Check out a sample textbook solution
Chapter 14 Solutions
Algebra and Trigonometry (MindTap Course List)
- Areas of Curved Regions the Monte Carlo method can be used to estimate the area under the graph of a function. The figure below shows the region under the graph of f(x)=x2 above the x-axis, between x=0 and x=1. if we choose a point in the square at random, probability that it lies under the graph of f(x)=x2 is the area under the graph divided by the area of the square. So if randomly select a large of points in the square, we have Modify the program from Problem 5 to carry out this Monte Carlo simulation and mate the required area.arrow_forwardAdvertising The effectiveness of a television commercial depends on many times a viewer watches it. After some experiments an advertising agency found that if the effectiveness E is measured on a scale of 0 to 10, then E(n)=23n190n2 where n is the number of tines a viewer watches a given commercial. Fer a commercial to have maximum effectiveness, how many times should a viewer watch it?arrow_forward
 College AlgebraAlgebraISBN:9781305115545Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
College AlgebraAlgebraISBN:9781305115545Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning Functions and Change: A Modeling Approach to Coll...AlgebraISBN:9781337111348Author:Bruce Crauder, Benny Evans, Alan NoellPublisher:Cengage Learning
Functions and Change: A Modeling Approach to Coll...AlgebraISBN:9781337111348Author:Bruce Crauder, Benny Evans, Alan NoellPublisher:Cengage Learning- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage



