
Depth of a Well One method for determining the depth of a well is to drop a stone into it and then measure the time it takes until the splash is heard. If d is the depth of the well (in feet) and t1, the time (in seconds) it takes for the stone to fall, then
How deep is the well if this total time is 3 s?
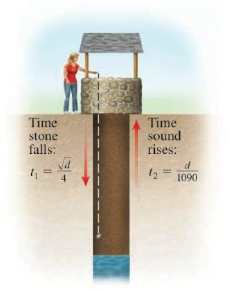
The depth of the well if the total time is 3 s.
Answer to Problem 119E
The depth of the well if the total time is 3 s is
Explanation of Solution
Given:
The total time elapsed between dropping the stone and hearing the splash is
Formula used:
Quadratic formula:
The solution of a quadratic equation of the form
Calculation:
Total time elapsed between dropping the stone and hearing the splash is
Substitute
Let
Use Quadratic formula to find value of x.
Substitute
Simplify the above equation as follows.
Note that, the distance can’t be negative.
Therefore,
Substitute
Thus, the depth of the well if the total time is 3 s is
Chapter 1 Solutions
Precalculus: Mathematics for Calculus - 6th Edition
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





