
Calculus: Early Transcendentals
8th Edition
ISBN: 9781285741550
Author: James Stewart
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Textbook Question
Chapter 15.2, Problem 58E
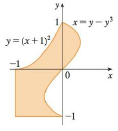
Express D as a union of regions of type I or type II and evaluate the
58.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Chapter 15 Solutions
Calculus: Early Transcendentals
Ch. 15.1 - (a) Estimate the volume of the solid that lies...Ch. 15.1 - If R = [0, 4] [1, 2], use a Riemann sum with m =...Ch. 15.1 - (a) Use a Riemann sum with m = n = 2 to estimate...Ch. 15.1 - (a) Estimate the volume of the solid that lies...Ch. 15.1 - Let V be the volume of the solid that lies under...Ch. 15.1 - A 20-ft-by-30-ft swimming pool is filled with...Ch. 15.1 - A contour map is shown for a function f on the...Ch. 15.1 - The contour map shows the temperature, in degrees...Ch. 15.1 - Evaluate the double integral by first identifying...Ch. 15.1 - Evaluate the double integral by first identifying...
Ch. 15.1 - Evaluate the double integral by first identifying...Ch. 15.1 - The integral R9y2dA, where R = [0, 4] [0, 2],...Ch. 15.1 - Find 02f(x,y)dxand 03f(x,y)dy 13. f(x, y) = x +...Ch. 15.1 - Find 02f(x,y)dxand 03f(x,y)dy 14.f(x,y)=yx+2Ch. 15.1 - Calculate the iterated integral. 15....Ch. 15.1 - Calculate the iterated integral. 16....Ch. 15.1 - Calculate the iterated integral. 17....Ch. 15.1 - Calculate the iterated integral. 18....Ch. 15.1 - Calculate the iterated integral. 19....Ch. 15.1 - Calculate the iterated integral. 20. 1315lnyxydydxCh. 15.1 - Calculate the iterated integral. 21....Ch. 15.1 - Calculate the iterated integral. 22. 0102yexydxdyCh. 15.1 - Calculate the iterated integral. 23....Ch. 15.1 - Calculate the iterated integral. 24....Ch. 15.1 - Calculate the iterated integral. 25....Ch. 15.1 - Calculate the iterated integral. 26. 0101s+tdsdtCh. 15.1 - Calculate the double integral. 27....Ch. 15.1 - Calculate the double integral. 28....Ch. 15.1 - Calculate the double integral. 29....Ch. 15.1 - Calculate the double integral. 30....Ch. 15.1 - Calculate the double integral. 31....Ch. 15.1 - Calculate the double integral. 32....Ch. 15.1 - Calculate the double integral. 33....Ch. 15.1 - Calculate the double integral. 34....Ch. 15.1 - Sketch the solid whose volume is given by the...Ch. 15.1 - Sketch the solid whose volume is given by the...Ch. 15.1 - Find the volume of the solid that lies under the...Ch. 15.1 - Find the volume of the solid that lies under the...Ch. 15.1 - Find the volume of the solid lying under the...Ch. 15.1 - Find the volume of the solid enclosed by the...Ch. 15.1 - Find the volume of the solid enclosed by the...Ch. 15.1 - Find the volume of the solid in the first octant...Ch. 15.1 - Find the volume of the solid enclosed by the...Ch. 15.1 - Graph the solid that lies between the surface z =...Ch. 15.1 - Find the average value of f over the given...Ch. 15.1 - Find the average value of f over the given...Ch. 15.1 - Prob. 49ECh. 15.1 - Use symmetry to evaluate the double integral. 50....Ch. 15.1 - Prob. 52ECh. 15.2 - Evaluate the iterated integral. 1. 1s0x(8x2y)dydxCh. 15.2 - Evaluate the iterated integral. 2. 020y2x2ydxdyCh. 15.2 - Evaluate the iterated integral. 3. 010yxey3dxdyCh. 15.2 - Evaluate the iterated integral. 4. 0/20xxsinydydxCh. 15.2 - Evaluate the iterated integral. 5....Ch. 15.2 - Evaluate the iterated integral. 6. 010ex1+exdwdvCh. 15.2 - Evaluate the double integral. 7....Ch. 15.2 - Evaluate the double integral. 8....Ch. 15.2 - Evaluate the double integral. 9....Ch. 15.2 - Evaluate the double integral. 10....Ch. 15.2 - Draw an example of a region that is (a) type I but...Ch. 15.2 - Draw an example of a region that is (a) both type...Ch. 15.2 - Express D as a region of type I and also as a...Ch. 15.2 - Express D as a region of type I and also as a...Ch. 15.2 - Set up iterated integrals for both orders of...Ch. 15.2 - Set up iterated integrals for both orders of...Ch. 15.2 - Evaluate the double integral. 17.DxcosydA, D is...Ch. 15.2 - Evaluate the double integral. 18. D(x2+2y)dA, D is...Ch. 15.2 - Evaluate the double integral. 19. Dy2dA, D is the...Ch. 15.2 - Evaluate the double integral. 20. DxydA, D is...Ch. 15.2 - Evaluate the double integral. 21. D(2xy)dA, D is...Ch. 15.2 - Evaluate the double integral. 22. DydA, D is the...Ch. 15.2 - Find the volume of the given solid. 23. Under the...Ch. 15.2 - Find the volume of the given solid. 24. Under the...Ch. 15.2 - Find the volume of the given solid. 25. Under the...Ch. 15.2 - Find the volume of the given solid. 26. Enclosed...Ch. 15.2 - Find the volume of the given solid. 27. The...Ch. 15.2 - Find the volume of the given solid. 28. Bounded by...Ch. 15.2 - Find the volume of the given solid. 29. Enclosed...Ch. 15.2 - Find the volume of the given solid. 30. Bounded by...Ch. 15.2 - Find the volume of the given solid. 31. Bounded by...Ch. 15.2 - Find the volume of the given solid. 32. Bounded by...Ch. 15.2 - Use a graphing calculator or computer to estimate...Ch. 15.2 - Find the approximate volume of the solid in the...Ch. 15.2 - Find the volume of the solid by subtracting two...Ch. 15.2 - Find the volume of the solid by subtracting two...Ch. 15.2 - Find the volume of the solid by subtracting two...Ch. 15.2 - Find the volume of the solid by subtracting two...Ch. 15.2 - Sketch the solid whose volume is given by the...Ch. 15.2 - Sketch the solid whose volume is given by the...Ch. 15.2 - Sketch the region of integration and change the...Ch. 15.2 - Sketch the region of integration and change the...Ch. 15.2 - Sketch the region of integration and change the...Ch. 15.2 - Sketch the region of integration and change the...Ch. 15.2 - Sketch the region of integration and change the...Ch. 15.2 - Sketch the region of integration and change the...Ch. 15.2 - Evaluate the integral by reversing the order of...Ch. 15.2 - Evaluate the integral by reversing the order of...Ch. 15.2 - Evaluate the integral by reversing the order of...Ch. 15.2 - Evaluate the integral by reversing the order of...Ch. 15.2 - Evaluate the integral by reversing the order of...Ch. 15.2 - Evaluate the integral by reversing the order of...Ch. 15.2 - Express D as a union of regions of type I or type...Ch. 15.2 - Express D as a union of regions of type I or type...Ch. 15.2 - Use Property 11 to estimate the value of the...Ch. 15.2 - Use Property 11 to estimate the value of the...Ch. 15.2 - Find the averge value of f over the region D. 61....Ch. 15.2 - Find the averge value of f over the region D. 62....Ch. 15.2 - Prove Property 11.Ch. 15.2 - In evaluating a double integral over a region D, a...Ch. 15.2 - Use geometry or symmetry, or both, to evaluate the...Ch. 15.2 - Use geometry or symmetry, or both, to evaluate the...Ch. 15.2 - Use geometry or symmetry, or both, to evaluate the...Ch. 15.2 - Use geometry or symmetry, or both, to evaluate the...Ch. 15.2 - Use geometry or symmetry, or both, to evaluate the...Ch. 15.3 - A region R is shown. Decide whether to use polar...Ch. 15.3 - A region R is shown. Decide whether to use polar...Ch. 15.3 - A region R is shown. Decide whether to use polar...Ch. 15.3 - A region R is shown. Decide whether to use polar...Ch. 15.3 - Sketch the region whose area is given by the...Ch. 15.3 - Sketch the region whose area is given by the...Ch. 15.3 - Evaluate the given integral by changing to polar...Ch. 15.3 - Evaluate the given integral by changing to polar...Ch. 15.3 - Evaluate the given integral by changing to polar...Ch. 15.3 - Evaluate the given integral by changing to polar...Ch. 15.3 - Evaluate the given integral by changing to polar...Ch. 15.3 - Evaluate the given integral by changing to polar...Ch. 15.3 - Evaluate the given integral by changing to polar...Ch. 15.3 - Evaluate the given integral by changing to polar...Ch. 15.3 - Use a double integral to find the area of the...Ch. 15.3 - Use a double integral to find the area of the...Ch. 15.3 - Use a double integral to find the area of the...Ch. 15.3 - Use a double integral to find the area of the...Ch. 15.3 - Use polar coordinates to find the volume of the...Ch. 15.3 - Use polar coordinates to find the volume of the...Ch. 15.3 - Use polar coordinates to find the volume of the...Ch. 15.3 - Use polar coordinates to find the volume of the...Ch. 15.3 - Use polar coordinates to find the volume of the...Ch. 15.3 - Use polar coordinates to find the volume of the...Ch. 15.3 - Use polar coordinates to find the volume of the...Ch. 15.3 - Use polar coordinates to find the volume of the...Ch. 15.3 - Use polar coordinates to find the volume of the...Ch. 15.3 - (a) A cylindrical drill with radius r1 is used to...Ch. 15.3 - Evaluate the iterated integral by converting to...Ch. 15.3 - Evaluate the iterated integral by converting to...Ch. 15.3 - Evaluate the iterated integral by converting to...Ch. 15.3 - Evaluate the iterated integral by converting to...Ch. 15.3 - Express the double integral in terms of a single...Ch. 15.3 - Express the double integral in terms of a single...Ch. 15.3 - A swimming pool is circular with a 40-ft diameter....Ch. 15.3 - An agricultural sprinkler distributes water in a...Ch. 15.3 - Find the average value of the function...Ch. 15.3 - Let D be the disk with center the origin and...Ch. 15.3 - Use polar coordinates to combine the sum...Ch. 15.3 - (a) We define the improper integral (over the...Ch. 15.3 - Use the result of Exercise 40 part (c) to evaluate...Ch. 15.4 - Electric charge is distributed over the rectangle...Ch. 15.4 - Electric charge is distributed over the disk x2 +...Ch. 15.4 - Find the mass and center of mass of the lamina...Ch. 15.4 - Find the mass and center of mass of the lamina...Ch. 15.4 - Find the mass and center of mass of the lamina...Ch. 15.4 - Find the mass and center of mass of the lamina...Ch. 15.4 - Find the mass and center of mass of the lamina...Ch. 15.4 - Find the mass and center of mass of the lamina...Ch. 15.4 - Find the mass and center of mass of the lamina...Ch. 15.4 - Find the mass and center of mass of the lamina...Ch. 15.4 - A lamina occupies the part of the disk x2 + y2 1...Ch. 15.4 - Find the center of mass of the lamina in Exercise...Ch. 15.4 - The boundary of a lamina consists of the...Ch. 15.4 - Find the center of mass of the lamina in Exercise...Ch. 15.4 - Find the center of mass of a lamina in the shape...Ch. 15.4 - A lamina occupies the region inside the circle x2...Ch. 15.4 - Find the moments of inertia Ix, Iy, I0 for the...Ch. 15.4 - Find the moments of inertia Ix, Iy, I0 for the...Ch. 15.4 - Find the moments of inertia Ix, Iy, lo for the...Ch. 15.4 - Prob. 20ECh. 15.4 - A lamina with constant density (x, y) = occupies...Ch. 15.4 - A lamina with constant density (x, y) = occupies...Ch. 15.4 - A lamina with constant density (x, y) = occupies...Ch. 15.4 - A lamina with constant density (x, y) = occupies...Ch. 15.4 - Prob. 27ECh. 15.4 - Prob. 28ECh. 15.4 - Prob. 29ECh. 15.4 - (a) A lamp has two bulbs, each of a type with...Ch. 15.4 - Xavier and Yolanda both have classes that end at...Ch. 15.4 - When studying the spread of an epidemic, we assume...Ch. 15.5 - Find the area of the surface. 1. The part of the...Ch. 15.5 - Find the area of the surface. 2. The part of the...Ch. 15.5 - Find the area of the surface. 3. The part of the...Ch. 15.5 - Find the area of the surface. 4. The part of the...Ch. 15.5 - Find the area of the surface. 5. The part of the...Ch. 15.5 - Find the area of the surface. 6. The part of the...Ch. 15.5 - Find the area of the surface. 7. The part of the...Ch. 15.5 - Find the area of the surface. 8. The surface...Ch. 15.5 - Find the area of the surface. 9. The part of the...Ch. 15.5 - Find the area of the surface. 10. The part of the...Ch. 15.5 - Find the area of the surface. 11. The part of the...Ch. 15.5 - Find the area of the surface. 12. The part of the...Ch. 15.5 - Find the area of the surface correct to four...Ch. 15.5 - Prob. 14ECh. 15.5 - Prob. 21ECh. 15.5 - If you attempt to use Formula 2 to find the area...Ch. 15.5 - Find the area of the finite part of the paraboloid...Ch. 15.5 - The figure shows the surface created when the...Ch. 15.6 - Evaluate the integral in Example 1, integrating...Ch. 15.6 - Evaluate the integral E(xy+z2)dv, where...Ch. 15.6 - Evaluate the iterated integral....Ch. 15.6 - Evaluate the iterated integral....Ch. 15.6 - Evaluate the iterated integral. 5....Ch. 15.6 - Evaluate the iterated integral. 6....Ch. 15.6 - Evaluate the iterated integral....Ch. 15.6 - Evaluate the iterated integral. 8....Ch. 15.6 - Evaluate the triple integral. 9. EydV, where...Ch. 15.6 - Evaluate the triple integral. 10.EezydV, where...Ch. 15.6 - Evaluate the triple integral. 11. Ezx2+z2dV, where...Ch. 15.6 - Evaluate the triple integral. 12. EsinydV, where E...Ch. 15.6 - Evaluate the triple integral. 13. E6xydV, where E...Ch. 15.6 - Evaluate the triple integral. 14. E(xy)dV, where E...Ch. 15.6 - Evaluate the triple integral. 15. Ty2dV. where T...Ch. 15.6 - Evaluate the triple integral. 16. TxzdV, where T...Ch. 15.6 - Evaluate the triple integral. 17. ExdV, where E is...Ch. 15.6 - Evaluate the triple integral. 18. EzdV, where E is...Ch. 15.6 - Use a triple integral to find the volume of the...Ch. 15.6 - Use a triple integral to find the volume of the...Ch. 15.6 - Use a triple integral to find the volume of the...Ch. 15.6 - Use a triple integral to find the volume of the...Ch. 15.6 - Use the Midpoint Rule for triple integrals...Ch. 15.6 - Prob. 26ECh. 15.6 - Sketch the solid whose volume is given by the...Ch. 15.6 - Sketch the solid whose volume is given by the...Ch. 15.6 - Express the integralEf(x,y,z)dV, as an iterated...Ch. 15.6 - Express the integral Ef(x,y,z)dV, as an iterated...Ch. 15.6 - Express the integral Ef(x,y,z)dV,as an iterated...Ch. 15.6 - Express the integral Ef(x,y,z)dV,as an iterated...Ch. 15.6 - The figure shows the region of integration for the...Ch. 15.6 - The figure shows the region of integration for the...Ch. 15.6 - Write five other iterated integrals that are equal...Ch. 15.6 - Write five other iterated integrals that are equal...Ch. 15.6 - Evaluate the triple integral using only geometric...Ch. 15.6 - Evaluate the triple integral using only geometric...Ch. 15.6 - Find the mass and center of mass of the solid E...Ch. 15.6 - Find the mass and center of mass of the solid R...Ch. 15.6 - Find the mass and center of mass of the solid E...Ch. 15.6 - Find the mass and center of mass of the solid F....Ch. 15.6 - Assume that the solid has constant density k. 43....Ch. 15.6 - Assume that the solid has constant density k. 44....Ch. 15.6 - Prob. 45ECh. 15.6 - Assume that the solid has constant density k. 46....Ch. 15.6 - Prob. 47ECh. 15.6 - Set up, but do not evaluate, integral expressions...Ch. 15.6 - Prob. 51ECh. 15.6 - Prob. 52ECh. 15.6 - The average value of a function f (x, y, z) over a...Ch. 15.6 - The average value of a function f (x, y, z) over a...Ch. 15.7 - Plot the point whose cylindrical coordinates are...Ch. 15.7 - Prob. 2ECh. 15.7 - Change from rectangular to cylindrical...Ch. 15.7 - Change from rectangular to cylindrical...Ch. 15.7 - Describe in words the surface whose equation is...Ch. 15.7 - Describe in words the surface whose equation is...Ch. 15.7 - Identify the surface whose equation is given. 7....Ch. 15.7 - Identify the surface whose equation is given. 8. r...Ch. 15.7 - Write the equations in cylindrical coordinates. 9....Ch. 15.7 - Write the equations in cylindrical coordinates....Ch. 15.7 - Sketch the solid described by the given...Ch. 15.7 - Sketch the solid described by the given...Ch. 15.7 - A cylindrical shell is 20 cm long, with inner...Ch. 15.7 - Use a graphing device to draw the solid enclosed...Ch. 15.7 - Sketch the solid whose volume is given by the...Ch. 15.7 - Sketch the solid whose volume is given by the...Ch. 15.7 - Use cylindrical coordinates. 17. Evaluate...Ch. 15.7 - Use cylindrical coordinates. 18. EvaluateEZdV,...Ch. 15.7 - Use cylindrical coordinates. 19. Evaluate...Ch. 15.7 - Use cylindrical coordinates. 20. EvaluateE(xy)dV,...Ch. 15.7 - Use cylindrical coordinates. 21. Evaluate Ex2dV,...Ch. 15.7 - Use cylindrical coordinates. 22. Find the volume...Ch. 15.7 - Use cylindrical coordinates. 23. Find the volume...Ch. 15.7 - Use cylindrical coordinates. 24. Find the volume...Ch. 15.7 - Use cylindrical coordinates. 25. (a) Find the...Ch. 15.7 - Use cylindrical coordinates. 26. (a) Find the...Ch. 15.7 - Use cylindrical coordinates. 27. Find the mass and...Ch. 15.7 - Use cylindrical coordinates. 28. Find the mass of...Ch. 15.7 - Evaluate the integral by changing to cylindrical...Ch. 15.7 - Evaluate the integral by changing to cylindrical...Ch. 15.7 - When studying the formation of mountain ranges,...Ch. 15.8 - Prob. 1ECh. 15.8 - Prob. 2ECh. 15.8 - Prob. 3ECh. 15.8 - Change from rectangular to spherical coordinates....Ch. 15.8 - Describe in words the surface whose equation is...Ch. 15.8 - Describe in words the surface whose equation is...Ch. 15.8 - Identify the surface whose equation is given. 7. ...Ch. 15.8 - Identify the surface whose equation is given. 8. =...Ch. 15.8 - Write the equation in spherical coordinates. 9....Ch. 15.8 - Write the equation in spherical coordinates. 10....Ch. 15.8 - Sketch the solid described by the given...Ch. 15.8 - Sketch the solid described by the given...Ch. 15.8 - Sketch the solid described by the given...Ch. 15.8 - Sketch the solid described by the given...Ch. 15.8 - A solid lies above the cone z = x2+y2 and below...Ch. 15.8 - (a) Find inequalities that describe a hollow ball...Ch. 15.8 - Sketch the solid whose volume is given by the...Ch. 15.8 - Sketch the solid whose volume is given by the...Ch. 15.8 - Set up the triple integral of an arbitrary of an...Ch. 15.8 - Set up the triple integral of an arbitrary of an...Ch. 15.8 - Use spherical coordinates. 21. Evaluate B (x2+y2 +...Ch. 15.8 - Use spherical coordinates. 22. Evaluate E y2z2 dV,...Ch. 15.8 - Use spherical coordinates. 23. Evaluate E (x2 +...Ch. 15.8 - Use spherical coordinates. 24. Evaluate E y2 dV,...Ch. 15.8 - Use spherical coordinates. 25. Evaluate E xe x2 +...Ch. 15.8 - Use spherical coordinates. 26. Evaluate E...Ch. 15.8 - Use spherical coordinates. 27. Find the volume of...Ch. 15.8 - Use spherical coordinates. 28. Find the average...Ch. 15.8 - Use spherical coordinates. 29. (a) Find the volume...Ch. 15.8 - Use spherical coordinates. 30. Find the volume of...Ch. 15.8 - Use spherical coordinates. 31. (a) Find the...Ch. 15.8 - Use spherical coordinates. 32. Let H be a solid...Ch. 15.8 - Use spherical coordinates. 33. (a) Find the...Ch. 15.8 - Use spherical coordinates. 34. Find the mass and...Ch. 15.8 - Use cylindrical or spherical coordinates,...Ch. 15.8 - Use cylindrical or spherical coordinates,...Ch. 15.8 - Prob. 37ECh. 15.8 - Prob. 38ECh. 15.8 - Evaluate the integral by changing to spherical...Ch. 15.8 - Evaluate the integral by changing to spherical...Ch. 15.8 - Evaluate the integral by changing to spherical...Ch. 15.8 - A model for the density of the earths atmosphere...Ch. 15.8 - Prob. 45ECh. 15.8 - Prob. 46ECh. 15.8 - Show that x2+y2+z2e-(x2+y2+z2) dx dy dz = 2 (The...Ch. 15.8 - (a) Use cylindrical coordinates to show that the...Ch. 15.9 - Find the Jacobian of the transformation. 1. x = 2u...Ch. 15.9 - Find the Jacobian of the transformation. 2. x = u2...Ch. 15.9 - Prob. 3ECh. 15.9 - Find the Jacobian of the transformation. 4. x =...Ch. 15.9 - Find the Jacobian of the transformation. 5. x =...Ch. 15.9 - Find the Jacobian of the transformation. 6. x = u...Ch. 15.9 - Find the image of the set S under the given...Ch. 15.9 - Find the image of the set S under the given...Ch. 15.9 - Find the image of the set S under the given...Ch. 15.9 - Find the image of the set S under the given...Ch. 15.9 - A region R in the xy-plane is given. Find...Ch. 15.9 - Prob. 12ECh. 15.9 - A region R in the xy-plane is given. Find...Ch. 15.9 - A region R in the xy-plane is given. Find...Ch. 15.9 - Use the given transformation to evaluate the...Ch. 15.9 - Use the given transformation to evaluate the...Ch. 15.9 - Use the given transformation to evaluate the...Ch. 15.9 - Use the given transformation to evaluate the...Ch. 15.9 - Use the given transformation to evaluate the...Ch. 15.9 - Prob. 20ECh. 15.9 - (a) Evaluate E dV, where E is the solid enclosed...Ch. 15.9 - An important problem in thermodynamics is to find...Ch. 15.9 - Evaluate the integral by making an appropriate...Ch. 15.9 - Evaluate the integral by making an appropriate...Ch. 15.9 - Evaluate the integral by making an appropriate...Ch. 15.9 - Evaluate the integral by making an appropriate...Ch. 15.9 - Evaluate the integral by making an appropriate...Ch. 15.9 - Let f be continuous oil [0, 1] and letRbe the...Ch. 15 - Prob. 1RCCCh. 15 - Prob. 2RCCCh. 15 - How do you change from rectangular coordinates to...Ch. 15 - If a lamina occupies a plane region D and has...Ch. 15 - Prob. 5RCCCh. 15 - Prob. 6RCCCh. 15 - Prob. 7RCCCh. 15 - Prob. 8RCCCh. 15 - Prob. 9RCCCh. 15 - Prob. 10RCCCh. 15 - Prob. 1RQCh. 15 - Prob. 2RQCh. 15 - Prob. 3RQCh. 15 - Prob. 4RQCh. 15 - Prob. 5RQCh. 15 - Determine whether the statement is true or false....Ch. 15 - Determine whether the statement is true or false....Ch. 15 - Prob. 8RQCh. 15 - Prob. 9RQCh. 15 - A contour map is shown for a function f on the...Ch. 15 - Use the Midpoint Rule to estimate the integral in...Ch. 15 - Calculate the iterated integral. 3....Ch. 15 - Calculate the iterated integral. 4. 0101yexydxdyCh. 15 - Calculate the iterated integral. 5....Ch. 15 - Calculate the iterated integral. 6. 01xex3xy2dydxCh. 15 - Calculate the iterated integral. 7....Ch. 15 - Calculate the iterated integral. 8....Ch. 15 - Write Rf(x,y)dA as an iterated integral, where R...Ch. 15 - Write Rf(x,y)dA as an iterated integral, where R...Ch. 15 - The cylindrical coordinates of a point are (23,3,...Ch. 15 - Prob. 12RECh. 15 - The spherical coordinates of a point are (8, /4,...Ch. 15 - Identify the surfaces whose equations are given....Ch. 15 - Write the equation in cylindrical coordinates and...Ch. 15 - Prob. 16RECh. 15 - Describe the region whose area is given by the...Ch. 15 - Describe the solid whose volume is given by the...Ch. 15 - Calculate the iterated integral by first reversing...Ch. 15 - Calculate the iterated integral by first reversing...Ch. 15 - Calculate the value of the multiple integral. 21....Ch. 15 - Calculate the value of the multiple integral. 22....Ch. 15 - Calculate the value of the multiple integral. 23....Ch. 15 - Calculate the value of the multiple integral. 24....Ch. 15 - Calculate the value of the multiple integral. 25....Ch. 15 - Calculate the value of the multiple integral. 26....Ch. 15 - Calculate the value of the multiple integral. 27....Ch. 15 - Calculate the value of the multiple integral. 28....Ch. 15 - Calculate the value of the multiple integral. 29....Ch. 15 - Prob. 30RECh. 15 - Calculate the value of the multiple integral. 31....Ch. 15 - Calculate the value of the multiple integral. 32....Ch. 15 - Calculate the value of the multiple integral. 33....Ch. 15 - Prob. 34RECh. 15 - Prob. 35RECh. 15 - Prob. 36RECh. 15 - Prob. 37RECh. 15 - Prob. 38RECh. 15 - Prob. 39RECh. 15 - Prob. 40RECh. 15 - Consider a lamina that occupies the region D...Ch. 15 - A lamina occupies the part of the disk x2 + y2 a2...Ch. 15 - (a) Find the centroid of a solid right circular...Ch. 15 - Find the area of the part of the cone z2 = a2(x2 +...Ch. 15 - Prob. 45RECh. 15 - Use polar coordinates to evaluate...Ch. 15 - Use spherical coordinates to evaluate...Ch. 15 - Prob. 49RECh. 15 - Prob. 51RECh. 15 - A lamp has three bulbs, each of a type with...Ch. 15 - Prob. 53RECh. 15 - Prob. 54RECh. 15 - Prob. 55RECh. 15 - Use the transformation x = u2, y = v2 z = w2 to...Ch. 15 - Prob. 57RECh. 15 - The Mean Value Theorem for double integrals says...Ch. 15 - Prob. 59RECh. 15 - Prob. 60RECh. 15 - Prob. 1PCh. 15 - Evaluate the integral 0101emaxx2,y2dydxwhere...Ch. 15 - Prob. 3PCh. 15 - Prob. 4PCh. 15 - The double integral 010111xydxdyis an improper...Ch. 15 - Leonhard Euler was able to find the exact sum of...Ch. 15 - Prob. 7PCh. 15 - Prob. 8PCh. 15 - (a) Show that when Laplaces equation...Ch. 15 - (a) A lamina has constant density and takes the...Ch. 15 - If f is continuous, show that...Ch. 15 - Evaluate limnn2i=1nj=1n21n2+ni+j.Ch. 15 - The plane xa+yb+zc=1a0,b0,c0cuts the solid...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Recommended textbooks for you
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning

Calculus: Early Transcendentals
Calculus
ISBN:9781285741550
Author:James Stewart
Publisher:Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:9780134438986
Author:Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:9780134763644
Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:9781319050740
Author:Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:W. H. Freeman


Calculus: Early Transcendental Functions
Calculus
ISBN:9781337552516
Author:Ron Larson, Bruce H. Edwards
Publisher:Cengage Learning
Double and Triple Integrals; Author: Professor Dave Explains;https://www.youtube.com/watch?v=UubU3U2C8WM;License: Standard YouTube License, CC-BY