
Concept explainers
To graph: The equations
Explanation of Solution
Given information:
The equations
Graph:
The graph of the equation
| 0 | |
| 2 | |
| 4 |
The graph of equation is provided below,
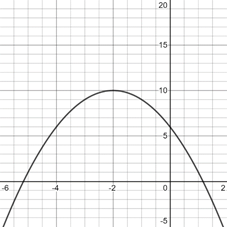
The graph of the equation
| 0 | |
| 2 | |
The graph of equation is provided below,
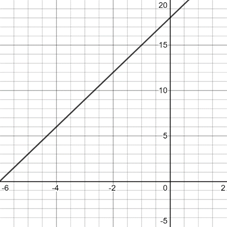
The graph of both equations in same figure is provided below,
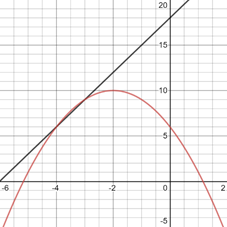
From the graph it looks as the graphs intersect near the
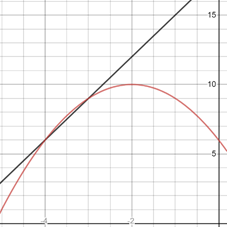
Since, the graphs intersect each other at 2 points.
Thus, the graphs intersect in the given viewing rectangle. There are 2 intersection points.
Interpretation:
The graph of an equation in a viewing screen is a viewing rectangle.
The
The
Then, the display portion of the graph lies in the rectangle
The equations
Chapter 1 Solutions
Precalculus: Mathematics for Calculus - 6th Edition
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





