
a.
To calculate: The equation
a.
Answer to Problem 3E
The solution of the equation
Explanation of Solution
Given information:
The equation
Formula used:
Steps to use this method to solve a quadratic polynomial
Step 1. Check the equation for real numbers which satisfy the equation that means the value of
Step 2. Check the equation for
Step 3. Now get the real roots of the equation.
Calculation:
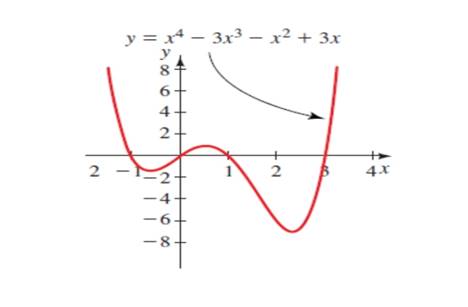
The graph of the equation
So find the real roots of the equation
Rewrite the equation
Check for the real number
The value of
Now check for real number
The real no
Now check for real number
The real no
Now check for real number
The real number
Now check for real number
The real no
Now we get the four real roots
The solution of the equation
b.
To calculate: The solution of the inequality
b.
Answer to Problem 3E
The solution of the inequality
Explanation of Solution
Given information:
The inequality
Formula used:
Steps to use this method to solve a quadratic polynomial
Step 1. Check the equation for real numbers which satisfy the equation that means the value of
Step 2. Check the equation for
Step 3. Now get the real roots of the equation.
Calculation:
The graph of the equation
So find the roots of the equation
Rewrite the equation
Check for the real number
The value of
Now check for real number
The real no
Now check for real number
The real no
Now check for real number
The real number
Now check for real number
The real no
Now we get the four real roots
The solution of the equation
The solution of the inequality consist of intervals
Thus, the solution of the inequality
Chapter 1 Solutions
Precalculus: Mathematics for Calculus - 6th Edition
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





