
College Physics
11th Edition
ISBN: 9781305952300
Author: Raymond A. Serway, Chris Vuille
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Concept explainers
Textbook Question
Chapter 19, Problem 74AP
A straight wire of mass 10.0 g and length 5.0 cm is suspended from two identical springs that, in turn, form a closed circuit (Fig. P19.74). The springs stretch a distance of 0.50 cm under the weight of the wire. The circuit has a total resistance of 12 Ω. When a magnetic field directed out of the page (indicated by the dots in the Figure) is turned on, the springs are observed to stretch an additional 0.30 cm. What is the strength of the magnetic field? (The upper portion of the circuit is fixed.)
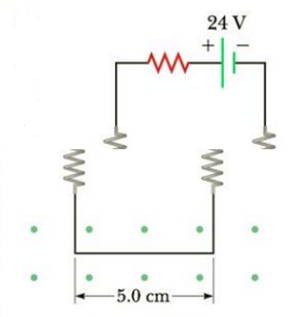
Figure P19.74
Expert Solution & Answer
Trending nowThis is a popular solution!

Chapter 19 Solutions
College Physics
Ch. 19.3 - A charged particle moves in a straight line...Ch. 19.3 - The north-pole end of a bar magnet is held near a...Ch. 19.5 - As a charged particle moves freely in a circular...Ch. 19.6 - A square and a circular loop with the same area...Ch. 19.8 - Which of the following actions would double the...Ch. 19.8 - Prob. 19.6QQCh. 19 - Prob. 1CQCh. 19 - Prob. 2CQCh. 19 - How can the motion of a charged particle be used...Ch. 19 - Prob. 4CQ
Ch. 19 - The following statements are related to the force...Ch. 19 - Will a nail be attracted to either pole of a...Ch. 19 - Figure CQ19.7 shows a coaxial cable carrying...Ch. 19 - A magnet attracts a piece of iron. The iron can...Ch. 19 - Figure CQ19.9 shows four positive charges, A, B,...Ch. 19 - Is the magnetic field created by a current loop...Ch. 19 - Suppose you move along a wire at the same speed as...Ch. 19 - Why do charged particles from outer space, called...Ch. 19 - A hanging Slinky toy is attached to a powerful...Ch. 19 - How can a current loop he used to determine the...Ch. 19 - Prob. 15CQCh. 19 - Figure CQ19.16 shows four permanent magnets, each...Ch. 19 - Two charged particles are projected in the same...Ch. 19 - Prob. 18CQCh. 19 - A magnetic field exerts a torque on each of the...Ch. 19 - Consider an electron near the Earths equator. In...Ch. 19 - (a) Find the direction of the force on a proton (a...Ch. 19 - Find the direction of the magnetic field acting on...Ch. 19 - Prob. 4PCh. 19 - A laboratory electromagnet produces a magnetic...Ch. 19 - Prob. 6PCh. 19 - Electrons and protons travel from the Sun to the...Ch. 19 - An oxygen ion (O+) moves in the xy-plane with a...Ch. 19 - A proton moving at 4.00 106 m/s through a...Ch. 19 - Sodium ions (Na+) move at 0.851 m/s through a...Ch. 19 - At the equator, near the surface of Earth, the...Ch. 19 - A proton travels with a speed of 5.02 106 m/s at...Ch. 19 - An electron moves in a circular path perpendicular...Ch. 19 - Figure P19.14a is a diagram of a device called a...Ch. 19 - Prob. 15PCh. 19 - A mass spectrometer is used to examine the...Ch. 19 - Jupiters magnetic field occupies a volume of space...Ch. 19 - Electrons in Earths upper atmosphere have typical...Ch. 19 - Prob. 19PCh. 19 - A proton (charge +e, mass mp), a deuteron (charge...Ch. 19 - A particle passes through a mass spectrometer as...Ch. 19 - In Figure P19.2, assume in each case the velocity...Ch. 19 - A current I = 15 A is directed along the positive...Ch. 19 - A straight wire carrying a 3.0-A current is placed...Ch. 19 - In Figure P19.3, assume in each case the velocity...Ch. 19 - A wire having a mass per unit length of 0.500 g/cm...Ch. 19 - A wire carries a current of 10.0 A in a direction...Ch. 19 - At a certain location, Earth has a magnetic field...Ch. 19 - A wire with a mass of 1.00 g/cm is placed on a...Ch. 19 - Mass m = 1.00 kg is suspended vertically at rest...Ch. 19 - Consider the system pictured in Figure P19.31. A...Ch. 19 - A metal rod of mass m carrying a current I glides...Ch. 19 - In Figure P19.33, the cube is 40.0 cm on each...Ch. 19 - A horizontal power line of length 58 m carries a...Ch. 19 - A wire is formed into a circle having a diameter...Ch. 19 - A current of 17.0 mA is maintained in a single...Ch. 19 - An eight-turn coil encloses an elliptical area...Ch. 19 - A current-carrying rectangular wire loop with...Ch. 19 - A 6.00-turn circular coil of wire is centered on...Ch. 19 - The orientation of small satellites is often...Ch. 19 - Along piece of wire with a mass of 0.100 kg and a...Ch. 19 - A rectangular loop has dimensions 0.500 m by 0.300...Ch. 19 - A lightning bolt may carry a current of 1.00 104...Ch. 19 - A long, straight wire going through the origin is...Ch. 19 - Neurons in our bodies carry weak currents that...Ch. 19 - In 1962 measurements of the magnetic field of a...Ch. 19 - A cardiac pacemaker can be affected by a static...Ch. 19 - The two wires shown in Figure P19.48 are separated...Ch. 19 - Prob. 49PCh. 19 - Two long, parallel wires carry currents of I1 =...Ch. 19 - Two long, parallel wires carry currents of I1 =...Ch. 19 - Prob. 52PCh. 19 - The magnetic field 40.0 cm away from a long,...Ch. 19 - Prob. 54PCh. 19 - Prob. 55PCh. 19 - Prob. 56PCh. 19 - A wire with a weight per unit length of 0.080 N/m...Ch. 19 - In Figure P19.58 the current in the long, straight...Ch. 19 - A long solenoid that has 1.00 103 turns uniformly...Ch. 19 - Prob. 60PCh. 19 - It is desired to construct a solenoid that will...Ch. 19 - Certain experiments must be performed in the...Ch. 19 - Ail electron is moving at a speed of 1.0 104 in/s...Ch. 19 - Figure P19.64 is a setup that can be used to...Ch. 19 - Two coplanar and concentric circular loops of wire...Ch. 19 - An electron moves in a circular path perpendicular...Ch. 19 - Prob. 67APCh. 19 - A 0.200-kg metal rod carrying a current of 10.0 A...Ch. 19 - Using an electromagnetic flowmeter (Fig. P19.69),...Ch. 19 - A uniform horizontal wire with a linear mass...Ch. 19 - Prob. 71APCh. 19 - Two long, parallel wires, each with a mass per...Ch. 19 - Protons having a kinetic energy of 5.00 MeV are...Ch. 19 - A straight wire of mass 10.0 g and length 5.0 cm...Ch. 19 - A 1.00-kg ball having net charge Q = 5.00 C is...Ch. 19 - Two long, parallel conductors separated by 10.0 cm...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, physics and related others by exploring similar questions and additional content below.Similar questions
- A piece of insulated wire is shaped into a figure eight as shown in Figure P23.12. For simplicity, model the two halves of the figure eight as circles. The radius of the upper circle is 5.00 cm and that of the lower circle is 9.00 cm. The wire has a uniform resistance per unit length of 3.00 Ω/m. A uniform magnetic field is applied perpendicular to the plane of the two circles, in the direction shown. The magnetic field is increasing at a constant rate of 2.00 T/s. Find (a) the magnitude and (b) the direction of the induced current in the wire. Figure P23.12arrow_forwardReview. Figure P31.31 shows a bar of mass m that can slide without friction on a pair of rails separated by a distance and located on an inclined plane that makes an angle with respect to the ground. The resistance of the resistor is R. and a uniform magnetic field of magnitude H is directed downward, perpendicular to the ground, over the entire region through which the bar moves. With what constant speed v does the bar slide along the rails?arrow_forwardFigure P23.15 shows a top view of a bar that can slide on two frictionless rails. The resistor is R = 6.00 , and a 2.50-T magnetic field is directed perpendicularly downward, into the paper. Let = 1.20 m. (a) Calculate the applied force required to move the bar to the right at a constant speed of 2.00 m/s. (b) At what rate is energy delivered to the resistor? Figure P23.15 Problems 15 through 18.arrow_forward
- The bar in Figure OQ23.10 moves on rails to the right with a velocity v, and a uniform, constant magnetic field is directed out of the page. Which of the following statements are correct? More than one statement may be correct. (a) The induced current in the loop is zero. (b) The induced current in the loop is clockwise. (c) The induced current in the loop is counterclockwise. (d) An external force is required to keep the bar moving at constant speed. (e) No force is required to keep the bar moving at constant speed.arrow_forwardA square, flat loop of wire is pulled at constant velocity through a region of uniform magnetic field directed perpendicular to the plane of the loop as shown in Figure OQ23.9. Which of the following statements are correct? More than one statement may be correct. (a) Current is induced in the loop in the clockwise direction. (b) Current is induced in the loop in the counterclockwise direction. (c) No current is induced in the loop. (d) Charge separation occurs in the loop, with the top edge positive. (e) Charge separation occurs in the loop, with the top edge negative.arrow_forwardMass m = 1.00 kg is suspended vertically at rest by an insulating string connected to a circuit partially immersed in a magnetic field as in Figure P19.30. The magnetic field has magnitude Bin = 2.00 T and the length = 0.500 m. (a) Find the current I. (b) If = 115 V, find the required resistance R. Figure P19.30arrow_forward
- A circuit consists of a conducting movable bar and a light bulb connected to two conducting rails as shown in Figure OQ23.16. An external magnetic field is directed perpendicular to the plane of the circuit. Which of the following actions will make the bulb light up? More than one statement may be correct. (a) The bar is moved to the left. (b) The bar is moved to the right. (c) The magnitude of the magnetic field is increased. (d) The magnitude of the magnetic field is decreased. (e) The bar is lifted off the rails.arrow_forwardA rectangular conducting loop is placed near a long wire carrying a current I as shown in Figure OQ23.5. If I decreases in time, what can be said of the current induced in the loop? (a) The direction of the current depends on the size of the loop. (b) The current is clockwise. (c) The current is counterclockwise. (d) The current is zero. (e) Nothing can be said about the current in the loop without more information.arrow_forwardA rectangular coil consists of N = 100 closely wrapped turns and has dimensions a = 0.400 m and b = 0.300 m. The coil is hinged along the y axis, and its plane makes an angle = 30.0 with the x axis (Fig. P22.25). (a) What is the magnitude of the torque exerted on the coil by a uniform magnetic field B = 0.800 T directed in the positive x direction when the current is I = 1.20 A in the direction shown? (b) What is the expected direction of rotation of the coil? Figure P22.25arrow_forward
- A stiff spring with a spring constant of 1200.0 N/m is connected to a bar on a slide generator as shown in Figure P32.40. Assume the bar has length l = 60.0 cm and mass m = 0.75 kg, and it slides without friction. The bar connects to a U-shaped wire to form a loop that has width w = 40.0 cm and total resistance 25 and that sits in a uniform magnetic field B = 0.35 T. The bar is initially pulled 5.0 cm to the left and released so that it begins to oscillate. What is the induced current in the loop as a function of time, I(t)? (Ignore any effects due to the magnetic force on the oscillating bar.)arrow_forwardA metal rod of mass m slides without friction along two parallel horizontal rails, separated by a distance l and connected by a resistor R, as shown in Figure P23.15. A uniform vertical magnetic field of magnitude B is applied perpendicular to the plane of the paper. The applied force shown in the figure acts only for a moment, to give die rod a speed v. In terms of m, l, R, B, and v, find the distance the rod will then slide as it coasts to a stop.arrow_forwardA solenoid of area Asol produces a uniform magnetic field (Fig. P32.28; shown in cross section). The solenoids magnetic field points out of the page and is decreasing according to B = B0(t0/t)2. A single conducting loop of area Aloop and resistance R is coaxial with the solenoid, with Aloop Asol. Find an expression for the current in the loop. What does the sign of your answer mean?arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
 College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning

College Physics
Physics
ISBN:9781285737027
Author:Raymond A. Serway, Chris Vuille
Publisher:Cengage Learning

College Physics
Physics
ISBN:9781305952300
Author:Raymond A. Serway, Chris Vuille
Publisher:Cengage Learning

Principles of Physics: A Calculus-Based Text
Physics
ISBN:9781133104261
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning

Physics for Scientists and Engineers: Foundations...
Physics
ISBN:9781133939146
Author:Katz, Debora M.
Publisher:Cengage Learning

Physics for Scientists and Engineers with Modern ...
Physics
ISBN:9781337553292
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning

Physics for Scientists and Engineers
Physics
ISBN:9781337553278
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Magnets and Magnetic Fields; Author: Professor Dave explains;https://www.youtube.com/watch?v=IgtIdttfGVw;License: Standard YouTube License, CC-BY