
Concept explainers
Explain what each of the following means and illustrate with sketch.
(a)
(b)
(c)
(d)
(e)
(a)
To explain: The meaning of
Explanation of Solution
Result used:
Definition of limit:
Let
Graph:
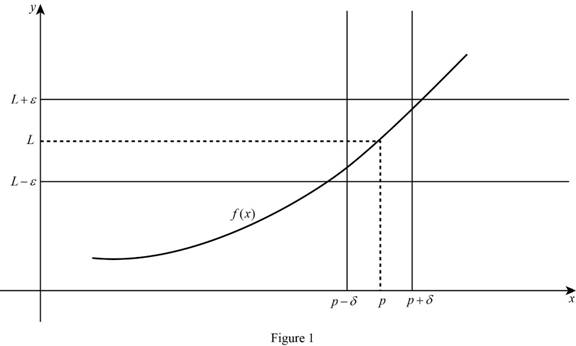
Calculation:
The limit of the function
In the limit definition
There are three cases for define
Case (1):
The limit of the function
Graph:
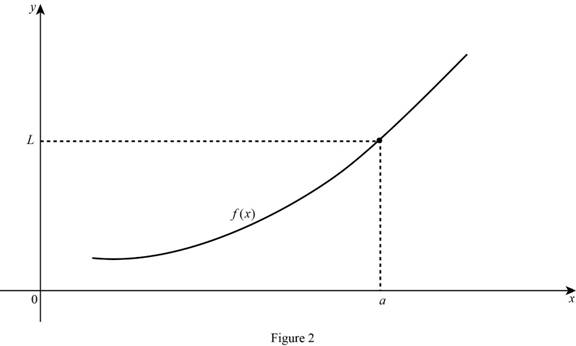
Case (2):
The limit of the function
Case (3):
The limit of the function
Graph:
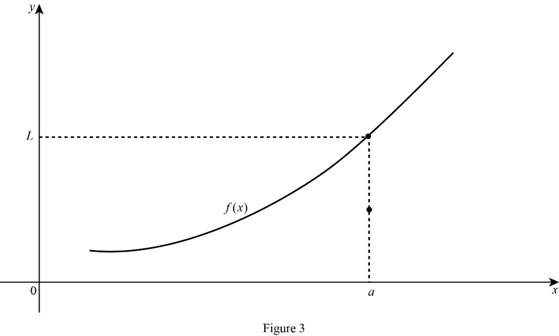
(b)
To explain: The meaning of
Explanation of Solution
Result used:
Definition of limit:
Let
Calculation:
Graph:
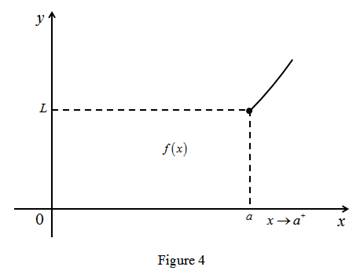
(c)
To explain: The meaning of
Explanation of Solution
Result used:
Definition of limit:
Let
Calculation:
The limit of the function
Graph:
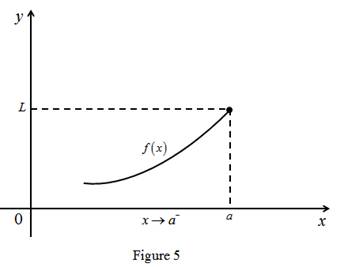
(d)
To explain: The meaning of
Explanation of Solution
Result used:
Definition of limit:
Let
Calculation:
The limit of the function
Graph:
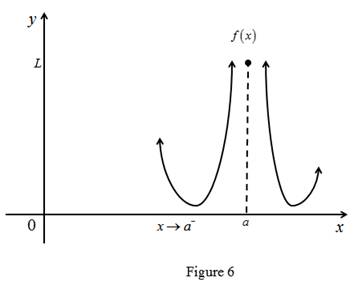
(e)
To explain: The meaning of
Explanation of Solution
Result used:
Definition of limit:
Let
Calculation:
The limit of the function
Graph:
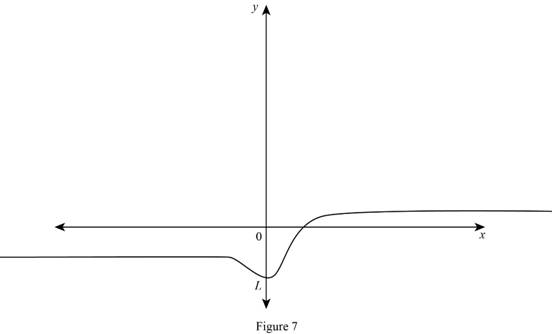
Want to see more full solutions like this?
Chapter 2 Solutions
Single Variable Calculus: Early Transcendentals
Additional Math Textbook Solutions
Precalculus: Concepts Through Functions, A Unit Circle Approach to Trigonometry (4th Edition)
Calculus, Single Variable: Early Transcendentals (3rd Edition)
Calculus and Its Applications (11th Edition)
University Calculus: Early Transcendentals (4th Edition)
Calculus For The Life Sciences
Advanced Mathematical Concepts: Precalculus with Applications, Student Edition
- Evaluate (a) lim (e(5+∆x) − e5)/∆x ∆x→0 (b) lim ((πx)2021 − 1)/π x − 1 x → 1/πarrow_forward1) Explain what it means to say that lim x → 4− f(x) = 3 and lim x → 4+ f(x) = 1. A)As x approaches 4 from the right, f(x) approaches 3. As x approaches 4 from the left, f(x) approaches 1. B)As x approaches 4 from the left, f(x) approaches 3. As x approaches 4 from the right, f(x) approaches 1. C)As x approaches 4, f(x) approaches 1, but f(4) = 3. D)As x approaches 4, f(x) approaches 3, but f(4) = 1. In this situation is it possible that lim x → 4 f(x) exists? Explain. A)Yes, f(x) could have a hole at (4, 3) and be defined such that f(4) = 1. B)Yes, f(x) could have a hole at (4, 1) and be defined such that f(4) = 3. C)Yes, if f(x) has a vertical asymptote at x = 4, it can be defined such that lim x→4− f(x) = 3, lim x→4+ f(x) = 1, and lim x→4 f(x) exists. D)No, lim x→4 f(x) cannot exist if lim x→4− f(x) ≠ lim x→4+ f(x).arrow_forwardFind f(2) and lim f(x)arrow_forward
- 1. Is it possible that f(2) = 5 but limx→2f(x) = 7? If so, what kind of function can satisfy this?arrow_forward(a) Estimate the value of lim x→ - infinity square root x^2+x+1 +1 by graphing the function f(x)=square root x^2+x+1 +1 b) use a table of values of f(x) to guess the value of the limit.arrow_forwardExplain what it means to say that lim x → 2− f(x) = 4 and lim x → 2+ f(x) = 9. As x approaches 2 from the right, f(x) approaches 4. As x approaches 2 from the left, f(x) approaches 9. As x approaches 2 from the left, f(x) approaches 4. As x approaches 2 from the right, f(x) approaches 9. As x approaches 2, f(x) approaches 9, but f(2) = 4. As x approaches 2, f(x) approaches 4, but f(2) = 9.arrow_forward
- The average monthly sales volume (in thousands of dollars) for a firm depends on the number of hours x of training of its sales staff, according to the following. (Give exact answers. Do not round.) S(x) = 2 x + 20 + x 2 , 2 ≤ x ≤ 100 (a) Find lim x→2+ S(x). thousand dollars(b) Find lim x→100− S(x). thousand dollarsarrow_forwardExamine the limits below and justify why they exist or not: lim f(x) = 4 and lim f(x) = −4 x→3− x→3+ lim f(x) = -5 and lim f(x) = -5 x→2− x→2+arrow_forward6. Given f(x)= { 3, if x < -2 x, if -2 ≤ x<8 x+3, if x≥8 estimate lim f(x) x→−2 a.-2 b. 1 c. does not exist d. 3 7. Using a table of values, estimate lim 1/ x-3 x→3 a. 1 b. -1 c. - ∞ d. ∞ 8. Using table of values, estimate lim x+4/ (x-5)2 x→5 a. 10 b. 8 c. - ∞ d. ∞arrow_forward
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





