
Bird Flight A bird is released from point A on an island, 5 mi from the nearest point B on a straight shoreline. The bird flies to a point C on the shoreline and then flies along the shoreline to its nesting area D (see the figure). Suppose the bird requires 10 kcal/mi of energy to fly over land and 14 kcal/mi to fly over water.
- (a) Use the fact that
to show that the total energy used by the bird is modeled by the function
- (b) If the bird instinctively chooses a path that minimizes its energy expenditure, to what point does it fly?
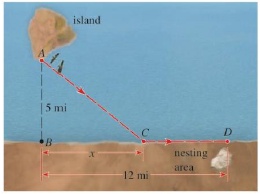
(a)
To show: The total energy used by the bird is
Explanation of Solution
Formula used:
Calculation:
The energy of the bird requires
All the distances related to the bird are given in the figure below,
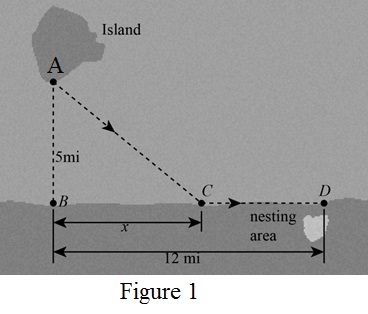
Let x be distance between point B and C.
In
Use the Pythagoras theorem to find the length AC.
The length of the side BD is 12mi and the length of the side BC is x mi.
Then, the length of the side CD is,
The bird flies from the point C to the point D on the land with the energy
To find the energy for
The bird flies from the point A to the point C on the water with the energy
To find the energy for
Then the total energy is,
Substitute
Thus, the total energy is
(b)
To find: The path that minimizes the energy expenditure.
Answer to Problem 31P
The bird flies till the point C on shoreline which is 5.013 miles from point B and then flies along the shoreline.
Explanation of Solution
From the part (a), the total energy is
To find the minimum energy sketch the graph of
The function contains the variable x is the length of the side BC.
The local minimum value of the function is the least finite value where the value of the function at the any number is less than to the original function.
The condition for local minimum is,
Using online graphing calculator, sketch the graph of the function
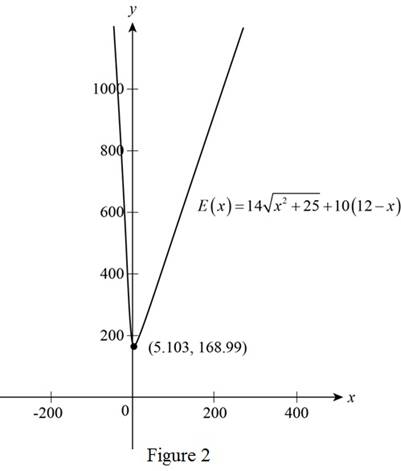
From the above figure, it can be observed that the least peak occurs at the point
Then, the minimum energy expenditure is 168.99 at
Thus, the point C is 5.103 mi away from point B.
Therefore, the bird flies till the point C on shoreline which is 5.013 miles from point B and then flies along the shoreline.
Chapter 2 Solutions
Precalculus: Mathematics for Calculus - 6th Edition
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





