
(a)
To find: The derivative of the function
(a)
Answer to Problem 37RE
The derivative of
Explanation of Solution
Formula used:
The derivative of a function f, denoted by
Calculation:
Obtain the derivative of the function
Compute
Multiply and divide
Since the limit h approaches zero but not equal to zero, cancel the common term h from both the numerator and the denominator,
Thus, the value of the derivative is
(b)
To find: The domain of f and
(b)
Answer to Problem 37RE
The domain of f is
Explanation of Solution
Calculation:
Obtain the domain of
Since square root is only defined for non-negative integers,
So, take
Thus, the domain of f is
Obtain the domain of
Since square root is only defined for non-negative integers and denominator is undefined at zero.
So, take
Thus, the domain of
(c)
To check: The answer to part (a) is reasonable by comparing the graphs of
(c)
Answer to Problem 37RE
The answer to part (a) is reasonable.
Explanation of Solution
Graph:
Use the online graphing calculator to draw the graph of
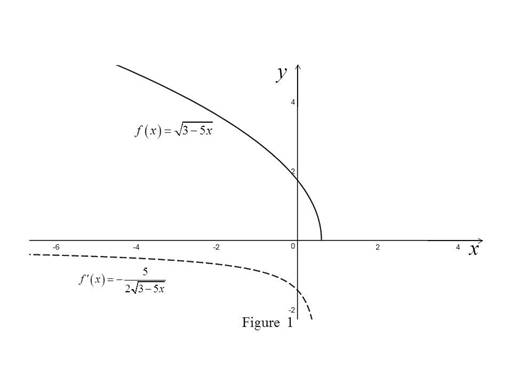
Observation:
From Figure 1, it is observed that the slope of the function
is always negative.
Also, the derivative graph
Thus, it can be concluded that the answer to part (a) is reasonable.
Chapter 2 Solutions
Single Variable Calculus: Concepts and Contexts, Enhanced Edition
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





