
Concept explainers
(a)
To find:The intervals in which
(a)
Answer to Problem 43RE
The function
Explanation of Solution
Given information:
The given graph is shown in figure ().
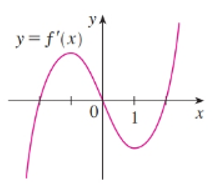
Figure (1)
Calculation:
If
If
From the above graph, the function
Therefore, the function
(b)
To find:The values of
(b)
Answer to Problem 43RE
The
Explanation of Solution
Given information:
The given graph is shown in figure ().
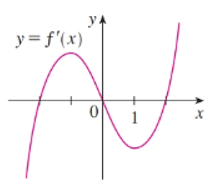
Figure (1)
Calculation:
The point at which
Here, at
Therefore, the
(c)
To find:Where is
(c)
Answer to Problem 43RE
The
Explanation of Solution
Given information:
The given graph is shown in figure (1).

Figure (1)
Calculation:
The function
Hence,
Therefore, the
(d)
To graph: For the function
(d)
Explanation of Solution
Given information:
The given graph is shown in figure (1).
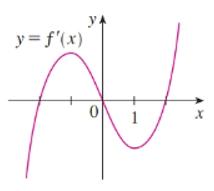
Figure (1)
Graph:
From the given figure that
Similarly,
It is known that
The graph for the function
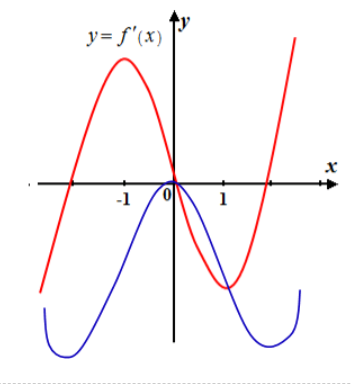
Figure (2)
The rough sketch of graph
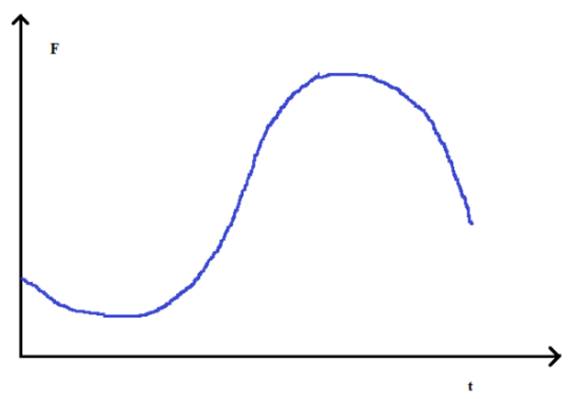
Figure (3)
Interpretation: Graph for the function
Chapter 2 Solutions
Single Variable Calculus: Concepts and Contexts, Enhanced Edition
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





