Chapter 2, Problem 4P

The figure shows a point P on the parabola y = x² and the point Q where the perpendicular bisector of OP intersects the y-axis. As P approaches the origin along the parabola, what happens to Q? Does it have a limiting position? If so, find it.

To determine

To find: The position of Q when P approaches to origin and the limiting position of Q.

Answer to Problem 4P

The limiting position of Q is $\underset{\_}{\left(0,\frac{1}{2}\right)}$.

Explanation of Solution

Result used:

Slope of Perpendicular lines: The product of slope of the two perpendicular lines equal to –1.

Graph:

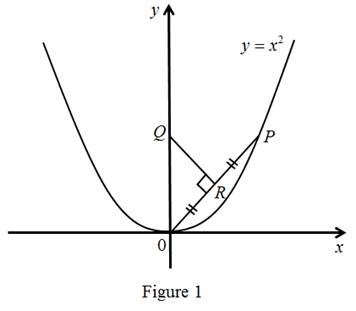
Calculation:

The perpendicular bisector of OP intersects the y-axis as P approaches the origin along the parabola then the length of the Q will increases and joins at a point R on the parabola.

Let R be the midpoint of $OP$, since $P\left(x,x^2\right)$ then $R\left(\frac{x}{2},\frac{x^2}{2}\right)$.

Let $Q\left(0,a\right)$ and from figure 1that is $OP\perp QR$.

The slope of $OP$ is

$\begin{array}{c}{m}_{OP}=\frac{x^2-0}{x-0}\\ =\frac{x^2}{x}\\ =x\end{array}$

By the slopes of the perpendicular lines

$\begin{array}{c}{m}_{QR}\times m_{OP}=-1\\ m_{QR}=\frac{-1}{m_{OP}}\end{array}$

$m_{QR}=\frac{1}{x}$ (1)

Let $Q\left(0,a\right)$,$R\left(\frac{x}{2},\frac{x^2}{2}\right)$ bet the two points then the slope of $QR$ is

$\begin{array}{c}{m}_{QR}=\frac{\frac{x^2}{2}-a}{\frac{x}{2}-0}\\ =\frac{\frac{x^2-2a}{2}}{\frac{x}{2}}\end{array}$

$m_{QR}=\frac{x^2-2a}{x}$ (2)

From equations (1) and (2)

$\begin{array}{c}-\frac{1}{x}=\frac{x^2-2a}{x}\\ -1=x^2-2a\\ 2a=x^2+1\\ a=\frac{x^2}{2}+\frac{1}{2}\end{array}$

In above equation if x approaches 0,

$\begin{array}{c}a=\frac{{\left(0\right)}^2}{2}+\frac{1}{2}\\ a=\frac{1}{2}\end{array}$

Thus the required limiting position of Q is $\underset{\_}{\left(0,\frac{1}{2}\right)}$.