
Concept explainers
(a)
To estimate: The value of the function when x approaches zero by graphing the function
(a)
Answer to Problem 25E
The estimated value of the function when x approaches zero
Explanation of Solution
Given:
The graph of the function
Draw the graph of the function
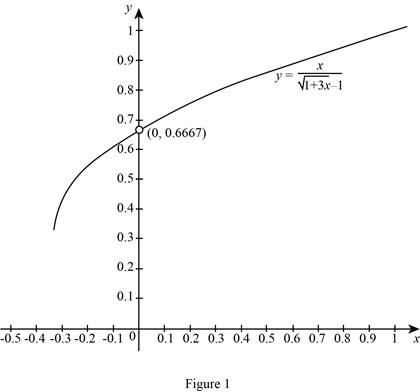
From the graph, as
That is,
Thus, the estimated value of
(b)
To guess: The value of the limit by using the table of values of
(b)
Answer to Problem 25E
The value of the limit by using the table of values of
Explanation of Solution
Calculation:
Make the table of values of
| x | ||
| −0.001 | ||
| −0.000 1 | ||
| −0.000 01 | ||
| −0.000 001 | ||
| 0.000 001 | ||
| 0.000 01 | ||
| 0.000 1 | ||
| 0.001 |
From the table, as x gets more close to 0, the value of
That is,
Thus, the limit appears to be
(c)
To prove: The limit value of the function is
(c)
Explanation of Solution
Given:
The limit of the function as x approaches 0 is
Limit Laws:
Suppose that c is a constant and the limits
Limit law 1:
Limit law 2:
Limit law 3:
Limit law 4:
Limit law 5:
Limit law 6:
Limit law 7:
Limit law 8:
Limit law 9:
Limit law 10:
Limit law 11:
Note 1:
The Quotient rule is not applicable directly for the function
Note 2:
“The limit may be infinite or it may be some finite value when both numerator and denominator approach 0.”
Calculation:
By note 3, take the limit x approaches 0 but
Simplify
Take the conjugate of the denominator and multiply and divide of
Use the difference of square formula,
Since the limit x approaches 0 but not equal to 0, cancel the common term
Use fact 1,
Use the limit laws to obtain the limit of the function as below:
Thus, the limit of the function is
Hence the required proof is obtained.
Chapter 2 Solutions
Single Variable Calculus: Concepts and Contexts, Enhanced Edition
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





