Physics for Scientists and Engineers
10th Edition
ISBN: 9781337553278
Author: Raymond A. Serway, John W. Jewett
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 23, Problem 41AP
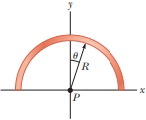
A line of positive charge is formed into a semicircle of radius R = 60.0 cm as shown in Figure P23.41. The charge per unit length along the semicircle is given by the expression λ = λ0 cos θ. The total charge on the semicircle is 12.0 μC. Calculate the total total on a charge of 3.00 μC placed at the center of curvature P.
Figure P23.41
Expert Solution & Answer
Trending nowThis is a popular solution!
Chapter 23 Solutions
Physics for Scientists and Engineers
Ch. 23.2 - Suppose a point charge is located at the center of...Ch. 23.3 - If the net flux through a gaussian surface is...Ch. 23 - A negatively charged rod of finite length carries...Ch. 23 - A positively charged disk has a uniform charge per...Ch. 23 - A uniformly charged ring of radius 10.0 cm has a...Ch. 23 - The electric field along the axis of a uniformly...Ch. 23 - Example 23.3 derives the exact expression for the...Ch. 23 - A uniformly charged rod of length L and total...Ch. 23 - A continuous line of charge lies along the x axis,...Ch. 23 - A thin rod of length and uniform charge per unit...
Ch. 23 - (a) Consider a uniformly charged, thin-walled,...Ch. 23 - A vertical electric field of magnitude 2.00 104...Ch. 23 - A flat surface of area 3.20 m2 is rotated in a...Ch. 23 - A nonuniform electric field is given by the...Ch. 23 - An uncharged, nonconducting, hollow sphere of...Ch. 23 - Find the net electric flux through the spherical...Ch. 23 - Four closed surfaces, S1 through S4 together with...Ch. 23 - A charge of 170 C is at the center of a cube of...Ch. 23 - (a) Find the net electric flux through the cube...Ch. 23 - A particle with charge of 12.0 C is placed at the...Ch. 23 - A particle with charge Q = 5.00 C is located at...Ch. 23 - A particle with charge Q is located at the center...Ch. 23 - (a) A panicle with charge q is located a distance...Ch. 23 - Find the net electric flux through (a) the closed...Ch. 23 - Figure P23.23 represents the top view of a cubic...Ch. 23 - Determine the magnitude of the electric field at...Ch. 23 - In nuclear fission, a nucleus of uranium-238,...Ch. 23 - Suppose you fill two rubber balloons with air,...Ch. 23 - A large, flat, horizontal sheet of charge has a...Ch. 23 - A nonconducting wall carries charge with a uniform...Ch. 23 - A uniformly charged, straight filament 7.00 m in...Ch. 23 - You are working on a laboratory device that...Ch. 23 - Consider a long, cylindrical charge distribution...Ch. 23 - Assume the magnitude of the electric field on each...Ch. 23 - A solid sphere of radius 40.0 cm has a total...Ch. 23 - A cylindrical shell of radius 7.00 cm and length...Ch. 23 - You are working for the summer at a research...Ch. 23 - You are working for the summer at a research...Ch. 23 - Find the electric flux through the plane surface...Ch. 23 - Three solid plastic cylinders all have radius 2.50...Ch. 23 - A line of charge starts at x = +x0 and extends to...Ch. 23 - Show that the maximum magnitude Emax of the...Ch. 23 - A line of positive charge is formed into a...Ch. 23 - A very large conducting plate lying in the xy...Ch. 23 - A sphere of radius R = 1.00 m surrounds a particle...Ch. 23 - A sphere of radius R surrounds a particle with...Ch. 23 - A slab of insulating material has a nonuniform...Ch. 23 - A sphere of radius 2a is made of a nonconducting...Ch. 23 - An infinitely long insulating cylinder of radius R...Ch. 23 - A particle with charge Q is located on the axis of...Ch. 23 - Review. A slab of insulating material (infinite in...Ch. 23 - Identical thin rods of length 2a carry equal...Ch. 23 - A solid insulating sphere of radius R has a...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, physics and related others by exploring similar questions and additional content below.Similar questions
- In Figure P24.49, a charged particle of mass m = 4.00 g and charge q = 0.250 C is suspended in static equilibrium at the end of an insulating thread that hangs from a very long, charged, thin rod. The thread is 12.0 cm long and makes an angle of 35.0 with the vertical. Determine the linear charge density of the rod. FIGURE P24.49arrow_forwardA conducting rod carrying a total charge of +9.00 C is bent into a semicircle of radius R = 33.0 cm, with its center of curvature at the origin (Fig.P24.75). The charge density along the rod is given by = 0 sin , where is measured clockwise from the +x axis. What is the magnitude of the electric force on a 1.00-C charged particle placed at the origin?arrow_forwardA solid insulating sphere of radius a = 5.00 cm carries a net positive charge of Q = 3.00 C uniformly distributed throughout its volume. Concentric with this sphere is a conducting spherical shell with inner radius b = 10.0 cm and outer radius c = 15.0 cm as shown in Figure P24.54, having net charge q = 1.00 C Prepare a graph of the magnitude of the electric field due to this configuration versus r for O r 25.0 cm.arrow_forward
- A uniform electric field given by E=(2.655.35j)105N/C permeates a region of space in which a small negatively charged sphere of mass 1.30 g is suspended by a light cord (Fig. P24.53). The sphere is found to be in equilibrium when the string makes an angle = 23.0. a. What is the charge on the sphere? b. What is the magnitude of the tension in the cord? FIGURE P24.53arrow_forwardA particle with charge Q = 5.00 C is located at the center of a cube of edge L = 0.100 m. In addition, six other identical charged particles having q = 1.00 C are positioned symmetrically around Q as shown in Figure P23.19. Determine the electric flux through one face of the cube. Figure P23.19 Problems 19 and 20.arrow_forwardA total charge Q is distributed uniformly on a metal ring of radius R. a. What is the magnitude of the electric field in the center of the ring at point O (Fig. P24.61)? b. What is the magnitude of the electric field at the point A lying on the axis of the ring a distance R from the center O (same length as the radius of the ring)? FIGURE P24.61arrow_forward
- Find an expression for the magnitude of the electric field at point A mid-way between the two rings of radius R shown in Figure P24.30. The ring on the left has a uniform charge q1 and the ring on the right has a uniform charge q2. The rings are separated by distance d. Assume the positive x axis points to the right, through the center of the rings. FIGURE P24.30 Problems 30 and 31.arrow_forwardA Two positively charged particles, each with charge Q, are held at positions (a, 0) and (a, 0) as shown in Figure P23.73. A third positively charged particle with charge q is placed at (0, h). a. Find an expression for the net electric force on the third particle with charge q. b. Show that the two charges Q behave like a single charge 2Q located at the origin when the distance h is much greater than a. Figure P23.73 Problems 73 and 74.arrow_forwardAssume the magnitude of the electric field on each face of the cube of edge L = 1.00 m in Figure P23.32 is uniform and the directions of the fields on each face are as indicated. Find (a) the net electric flux through the cube and (b) the net charge inside the cube. (c) Could the net charge he a single point charge? Figure P23.32arrow_forward
- Three small metallic spheres with identical mass m and identical charge +q are suspended by light strings from the same point (Fig. P23.55). The left-hand and right-hand strings have length L and make an angle with the vertical. What is the value of q in terms of k, g, m, L, and ? Figure P23.55arrow_forwardA circular ring of charge with radius b has total charge q uniformly distributed around it. What is the magnitude of the electric field at the center of the ring? (a) 0 (b) keq/b2 (c) keq2/b2 (d) keq2/b (e) none of those answersarrow_forwardA positively charged disk of radius R = 0.0366 m and total charge 56.8 C lies in the xz plane, centered on the y axis (Fig. P24.35). Also centered on the y axis is a charged ring with the same radius as the disk and a total charge of 34.1 C. The ring is a distance d = 0.0050 m above the disk. Determine the electric field at the point P on the y axis, where P is y = 0.0100 m above the origin. FIGURE P24.35 Problems 35 and 36.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers
Physics
ISBN:9781337553278
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...
Physics
ISBN:9781337553292
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...
Physics
ISBN:9781133939146
Author:Katz, Debora M.
Publisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...
Physics
ISBN:9781305116399
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Principles of Physics: A Calculus-Based Text
Physics
ISBN:9781133104261
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Electric Fields: Crash Course Physics #26; Author: CrashCourse;https://www.youtube.com/watch?v=mdulzEfQXDE;License: Standard YouTube License, CC-BY