
Concept explainers
Solve the following initial value problem over the interval from
(a) Analytically.
(b) Euler's method with
(c) Midpoint method with
(d) Fourth-order RK method with
(a)
To calculate: The solution of the initial value problem
Answer to Problem 1P
Solution:
The solution to the initial value problem is
Explanation of Solution
Given Information:
The initial value problem
Formula used:
Tosolve an initial value problem of the form
Calculation:
Rewrite the provided differential equation as,
Integrate both sides to get,
Now use the initial condition
Hence, the analytical solution of the initial value problem is
(b)
To calculate: The solution of the initial value problem
Answer to Problem 1P
Solution:
For
| t | y | |
| 0 | 1 | |
| 0.5 | 0.45 | |
| 1 | 0.25875 | |
| 1.5 | 0.245813 | 0.282684 |
| 2 | 0.387155 | 1.122749 |
And, for
| t | y | |
| 0 | 1 | |
| 0.25 | 0.725 | |
| 0.5 | 0.536593 | |
| 0.75 | 0.422861 | |
| 1 | 0.36603 | |
| 1.25 | 0.356879 | 0.165057 |
| 1.5 | 0.398143 | 0.457865 |
| 1.75 | 0.51261 | 1.005997 |
| 2 | 0.764109 | 2.215916 |
Explanation of Solution
Given Information:
The initial value problem
Formula used:
Solve an initial value problem of the form
Calculation:
From the initial condition
Let
Proceed further and use the following MATLAB code to implement Euler’s method and solve the differential equation.
Execute the above code to obtain the solutions for
| t | y | |
| 0 | 1 | |
| 0.5 | 0.45 | |
| 1 | 0.25875 | |
| 1.5 | 0.245813 | 0.282684 |
| 2 | 0.387155 | 1.122749 |
Now, the similar procedure can be followedfor the step size
The results thus obtained are tabulated as,
| t | y | |
| 0 | 1 | |
| 0.25 | 0.725 | |
| 0.5 | 0.536593 | |
| 0.75 | 0.422861 | |
| 1 | 0.36603 | |
| 1.25 | 0.356879 | 0.165057 |
| 1.5 | 0.398143 | 0.457865 |
| 1.75 | 0.51261 | 1.005997 |
| 2 | 0.764109 | 2.215916 |
The results for the two-step-sizes are plotted along with the analytical solution
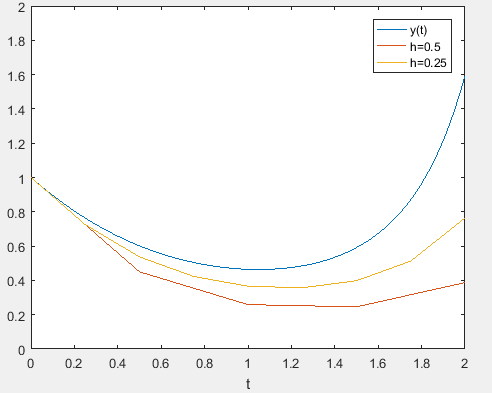
It is inferred that the smaller step-size would give a better approximation to the solution.
(c)
To calculate: The solution of the initial value problem
Answer to Problem 1P
Solution:
The solutions are tabulated as,
| t | y | |
| 0 | 1 | |
| 0.5 | 0.623906 | |
| 1 | 0.491862 | |
| 1.5 | 0.602762 | 0.693176 |
| 2 | 1.364267 | 3.956374 |
Explanation of Solution
Given Information:
The initial value problem
Formula used:
Solve an initial value problem of the form
Here,
Calculation:
From the initial condition
Let
Now,
Proceed further and use the following MATLAB code to implement mid-point iterative scheme and solve the differential equation.
Execute the above code to obtain the solutions tabulated as,
| t | Y | |
| 0 | 1 | |
| 0.5 | 0.623906 | |
| 1 | 0.491862 | |
| 1.5 | 0.602762 | 0.693176 |
| 2 | 1.364267 | 3.956374 |
The results for the are plotted along with the analytical solution
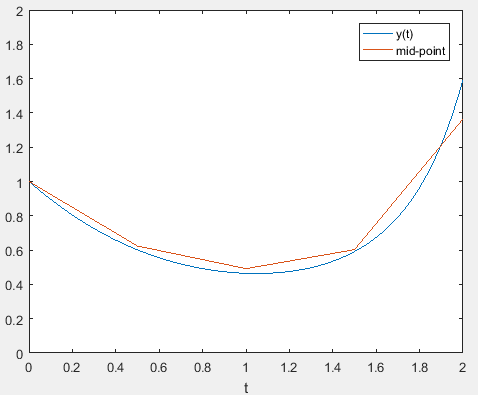
Thus, it is inferred that the mid-point method gives a good approximation to the solution.
(d)
To calculate: The solution of the initial value problem
Answer to Problem 1P
Solution:
The solutions are tabulated as,
| t | y | ||||
| 0 | 1 | ||||
| 0.5 | 0.6016 | ||||
| 1 | 0.4645 | 0.2095 | 0.2391 | 0.6717 | |
| 1.5 | 0.5914 | 0.6801 | 1.4953 | 1.8937 | 4.4609 |
| 2 | 1.5845 | 4.5949 | 10.8302 | 17.0071 | 51.9532 |
Explanation of Solution
Given Information:
The initial value problem
Formula used:
Solve an initial value problem of the form
In the above expression,
Calculation:
From the initial condition
Let
And,
And,
Therefore,
Proceed further and use the following MATLAB code to implement RK method of order four, solve the differential equation.
In an another .m file, define the equation as,
Execute the above code to obtain the solutions tabulated as,
| t | y | ||||
| 0 | 1 | ||||
| 0.5 | 0.6016 | ||||
| 1 | 0.4645 | 0.2095 | 0.2391 | 0.6717 | |
| 1.5 | 0.5914 | 0.6801 | 1.4953 | 1.8937 | 4.4609 |
| 2 | 1.5845 | 4.5949 | 10.8302 | 17.0071 | 51.9532 |
The results for the are plotted along with the analytical solution
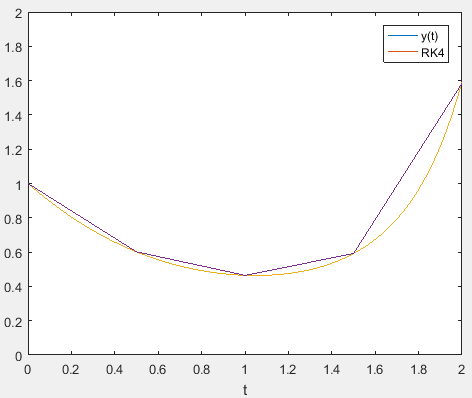
Hence, it is inferred that the RK method of order four gives the best approximation to the solution.
Want to see more full solutions like this?
Chapter 25 Solutions
NUMERICAL METH. F/ENGR.(LL)--W/ACCESS
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,






