Chapter 2.6, Problem 51E

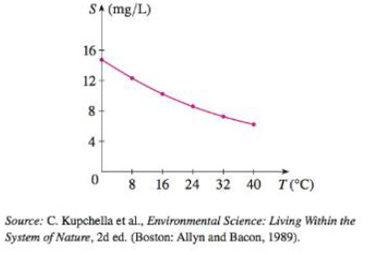
The quantity of oxygen that can dissolve in water depends on the temperature of the water. (So thermal pollution influences the oxygen content of water.) The graph shows how oxygen solubility S varies as a function of the water temperature T.

(a) What is the meaning of the derivative S'(T)? What are its units?

(b) Estimate the value of S'(16) and interpret it.

To determine

The derivative $S^{\prime }\left(T\right)$ and its unit.

Explanation of Solution

Given:

The quantity of oxygen that can dissolve in water depends on the temperature of the water.

Calculation:

The quantity of oxygen solubility S is depends on the water temperature T.

The quantity of oxygen solubility $S\left(T\right)$ is a function of the water temperature T.

Note that, the derivative $f^{\prime }\left(x\right)$ is the instantaneous rate of change of the function $f\left(x\right)$ with respect to x

The derivative $S^{\prime }\left(T\right)$ is the rate of change of quantity of oxygen solubility with respect to water temperature T.

The instantaneous rate of change is equal to $S^{\prime }\left(T\right)=\underset{\Delta x\to 0}{\lim }\frac{\Delta y}{\Delta t}\text{ here }y=S\left(T\right)$.

Here $\Delta y$ is measured in milligrams per liter and $\Delta t$ is measured in centigrade.

Thus, the units are milligrams per liter per centigrade.

Therefore, the unit are $\left(\text{mg/L}\right)/°\text{C}$.

To determine

To estimate: The value of $S^{\prime }\left(16\right)$.

Explanation of Solution

Estimate the value of $S^{\prime }\left(16\right)$.

Form given Figure, it is observed that the tangent line at 16 is passing through the point $\left(8,12\right)\text{ and }\left(24,8\right)$.

The slope of the tangent line to the curve at 16 as follows,

$\begin{array}{c}m=\frac{8-12}{24-8}\\ =\frac{-4}{16}\\ =-0.25\end{array}$

Thus, the slope of the tangent line to the curve at 16 is, $m=-0.25\left(\text{mg/L}\right)/°\text{C}$.

Note that, the slope of the tangent line to the curve at 16 is same $S^{\prime }\left(16\right)$.

Therefore, $S^{\prime }\left(16\right)=-0.25\left(\text{mg/L}\right)/°\text{C}$.

The derivative $S^{\prime }\left(16\right)=-0.25\left(\text{mg/L}\right)/°\text{C}$ means that the quantity of oxygen solubility decreasing at the rate of $0.25\left(\text{mg/L}\right)/°\text{C}$ as the temperature increasing post $16°\text{C}$.