Chapter 2.7, Problem 47E

To determine

To find: The first, second, third and fourth derivatives of the function $f\left(x\right)=2x^2-x^3$.

Answer to Problem 47E

The first, second, third and fourth derivatives of the function is $f^{\prime }\left(x\right)=4x-3x^2$, $f^{″}\left(x\right)=4-6x$, $f^{‴}\left(x\right)=4-6x$ and $f^{\left(4\right)}\left(x\right)=-6$.

Explanation of Solution

Given:

The function is, $f\left(x\right)=2x^2-x^3$.

Result Used:

The derivative of a function f is denoted by $f^{\prime }\left(x\right)$ is,

$f^{\prime }\left(x\right)=\underset{h\to 0}{\lim }\frac{f\left(x+h\right)-f\left(x\right)}{h}$ (1)

Calculation:

The first derivative of the function is computed as follows,

$\begin{array}{c}{f}^{\prime }\left(x\right)=\underset{h\to 0}{\lim }\frac{f\left(x+h\right)-f\left(x\right)}{h}\\ =\underset{h\to 0}{\lim }\frac{2{\left(x+h\right)}^2-{\left(x+h\right)}^3-\left\{2x^2-x^3\right\}}{h}\\ =\underset{h\to 0}{\lim }\frac{2x^2+2h^2+4xh-x^3-h^3-3x^{2}h-3x{h}^2-2x^2+x^3}{h}\\ =\underset{h\to 0}{\lim }\frac{2h^2+4xh-h^3-3x^{2}h-3x{h}^2}{h}\end{array}$

Simplified further to obtain the derivative of the function,

$\begin{array}{c}{f}^{\prime }\left(x\right)=\underset{h\to 0}{\lim }\left(2h+4x-h^2-3x^2-3xh\right)\\ =2\left(0\right)+4x-{\left(0\right)}^2-3x^2-3x\left(0\right)\\ =4x-3x^2\end{array}$

Therefore, the derivative of the function $f\left(x\right)$ is, $f^{\prime }\left(x\right)=4x-3x^2$.

The second derivative of the function is computed as follows,

$\begin{array}{c}{f}^{″}\left(x\right)={\left(f^{\prime }\left(x\right)\right)}^{\prime }\\ =\underset{h\to 0}{\lim }\frac{f^{\prime }\left(x+h\right)-f^{\prime }\left(x\right)}{h}\\ =\underset{h\to 0}{\lim }\frac{4\left(x+h\right)-3{\left(x+h\right)}^2-\left\{4x-3x^2\right\}}{h}\\ =\underset{h\to 0}{\lim }\frac{4x+4h-3x^2-3h^2-6xh-4x+3x^2}{h}\end{array}$

Simplify the expression and obtain the derivatives,

$\begin{array}{c}{f}^{″}\left(x\right)=\underset{h\to 0}{\lim }\frac{4h-3h^2-6xh}{h}\\ =\underset{h\to 0}{\lim }\left(4-3h-6x\right)\\ =4-3\left(0\right)-6x\\ =4-6x\end{array}$

Therefore, the second derivative of the function $f\left(x\right)$ is, $f^{″}\left(x\right)=4-6x$.

The third derivative of the function is computed as follows,

$\begin{array}{c}{f}^{‴}\left(x\right)={\left(f^{″}\left(x\right)\right)}^{\prime }\\ =\underset{h\to 0}{\lim }\frac{f^{″}\left(x+h\right)-f^{″}\left(x\right)}{h}\\ =\underset{h\to 0}{\lim }\frac{4-6\left(x+h\right)-\left\{4-6x\right\}}{h}\\ =\underset{h\to 0}{\lim }\frac{4-6x-6h-4+6x}{h}\end{array}$

Simplify the terms and obtain derivatives,

$\begin{array}{c}{f}^{‴}\left(x\right)=\underset{h\to 0}{\lim }\frac{-6h}{h}\\ =-6\underset{h\to 0}{\lim }\frac{h}{h}\\ =-6\underset{h\to 0}{\lim }1\\ =-6\end{array}$

Therefore, the third derivative of the function $f\left(x\right)$ is, $f^{‴}\left(x\right)=-6$.

The fourth derivative of the function is computed as follows,

$\begin{array}{c}{f}^{\left(4\right)}\left(x\right)={\left(f^{‴}\left(x\right)\right)}^{\prime }\\ =\underset{h\to 0}{\lim }\frac{f^{‴}\left(x+h\right)-f^{‴}\left(x\right)}{h}\\ =\underset{h\to 0}{\lim }\frac{-6-\left\{-6\right\}}{h}\\ =\underset{h\to 0}{\lim }\left(0\right)\end{array}$

$=0$

Thus, the fourth derivative of the function $f\left(x\right)$ is $f^{\left(4\right)}\left(x\right)=0$.

To sketch: The graph of the functions $f\left(x\right)$,$f^{\prime }\left(x\right)$,$f^{″}\left(x\right)$ and $f^{‴}\left(x\right)$ and explain the graphs consistent with the geometric interpretations of these derivatives.

The graphs are consistent with the geometric interpretations of these derivatives.

Graph:

Use the online graphing calculator to draw the functions $f\left(x\right),f^{\prime }\left(x\right),{f^{\prime }}^{\prime }\left(x\right),{{f^{\prime }}^{\prime }}^{\prime }\left(x\right)$ and $f^{\left(4\right)}\left(x\right)$ are shown below in Figure 1.

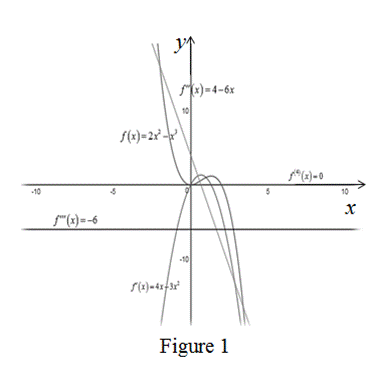
Geometrical Interpretation:

Take several points on the domain and estimate slope of the tangent to the function $f\left(x\right)$ which is same as the point of $f^{\prime }\left(x\right)$ at that point.

Thus, the derivative $f^{\prime }\left(x\right)$ is reasonable.

The $f^{\prime }\left(x\right)$ represents a quadratic function and $f^{″}\left(x\right)$ represents a linear function.

Take several points on the domain and estimate slope of the tangent to the function $f^{\prime }\left(x\right)$ which is same as the point of $f^{″}\left(x\right)$ at that point.

Therefore, the function $f^{″}\left(x\right)$ is reasonable.

The $f^{″}\left(x\right)$ represents a linear function and $f^{‴}\left(x\right)$ represents a constant function.

The straight line has same slope at all points. That is, $f^{″}\left(x\right)$ is constant value.

From the Figure 1, the estimated slope of the function $f^{″}\left(x\right)$ is $-6$ which is same as the derivative of $f^{″}\left(x\right)$. That is, $f^{‴}\left(x\right)=-6$.

Therefore, the function $f^{‴}\left(x\right)$ is reasonable.