
(a)
To find: The acceleration at
(a)
Answer to Problem 48E
At
Explanation of Solution
The graph of the position function is given with s in feet and t in seconds.
From the given graph, it is observed that the slope of the position function is always positive for
The slope of the curve increases very slowly initially, then just before
The slope of the curve increases very rapidly and then the increase in slope decreases just after
After the time just before
Graph:
Use the above information and trace the graph of velocity function as shown below in Figure 1.
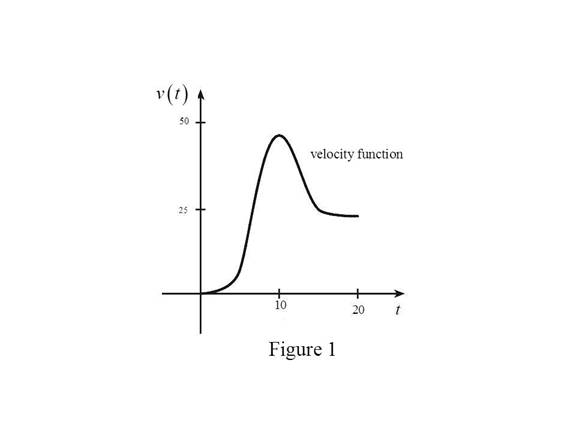
From Figure 1, it is observed that velocity contains the horizontal tangent at one point.
Let the point be A.
Note that, the value of the derivative will be zero at the point where the function has the horizontal tangent.
Thus, the graph of acceleration will be zero at the points A.
At
At
Use the above information and trace the graph of acceleration function as shown below in Figure 2.
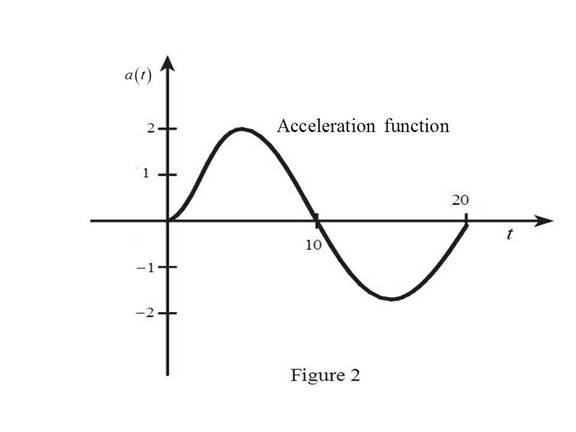
From Figure 2, it is observed that the acceleration is positive in the first half and negative in the second half.
From the Figure 2, at
(b)
To calculate: The jerk at
(b)
Answer to Problem 48E
The jerk at
Explanation of Solution
Estimation:
Draw the tangent at
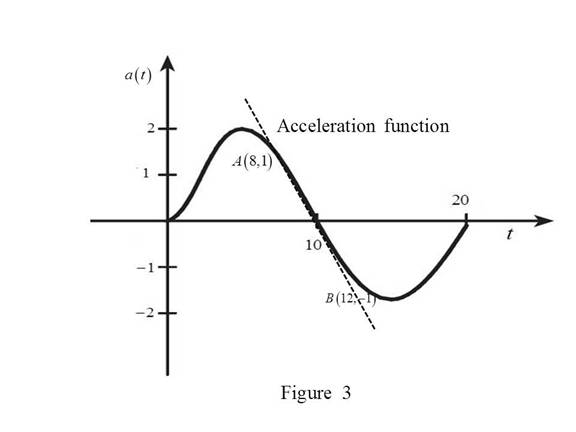
Calculation:
The jerk at
From the Figure 3, take two points in the vicinity of
Let these two point be A and B.
Slope of the curve at
Thus,
Therefore, the jerk at
Chapter 2 Solutions
Single Variable Calculus: Concepts and Contexts, Enhanced Edition
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





