
Concept explainers
Where is the greatest integer function f(x) = [[ x ]] not differentiable? Find a formula for[' and sketch its graph.
To find: The points where the greatest integer function
differentiable and then to find the formula for
Answer to Problem 52E
The greatest integer function is not differentiable at
The formula for the derivative function is
Explanation of Solution
Result Used:
The greatest integer function is defined as follows,
Calculation:
Obtain the points where the greatest integer function
The derivative of the greatest integer function is calculated as follows,
Case 1: x is not an integer.
Since x is not an integer,
Thus,
Case 2: x is an integer.
The left hand derivative of the function is computed as follows,
Since h approaches 0 from left,
This implies that,
Thus, the left hand derivative of the function does not exist. This follows that,
Therefore, the greatest integer function is not differentiable at the integer points.
By case (1) and (2), it is defined that the formula for the derivative is
Graph:
Use the above information and trace the graph of
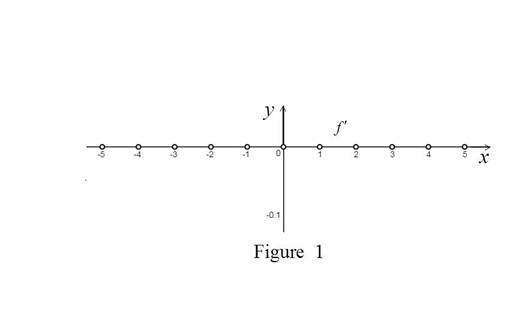
From the Figure 1, it is clear that the greatest integer function is discontinuous at integer points.
Chapter 2 Solutions
Single Variable Calculus: Concepts and Contexts, Enhanced Edition
Additional Math Textbook Solutions
Precalculus: A Unit Circle Approach
Precalculus (6th Edition)
Single Variable Calculus: Early Transcendentals (2nd Edition) - Standalone book
Calculus and Its Applications (11th Edition)
Precalculus Enhanced with Graphing Utilities (7th Edition)
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





