
Concept explainers
Trace or copy the graph of the given function .f. (Assume that the axes have equal scales.) Then use the method of Example 1 to sketch the graph of f' below it.
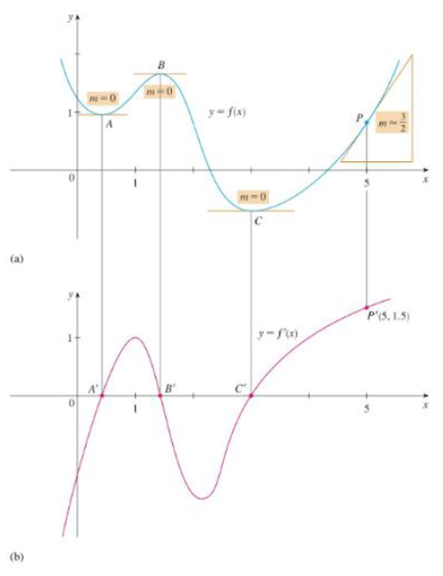
Example 1

FIGURE 1
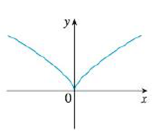
FIGURE 2
To sketch: The graph of
Explanation of Solution
From the point A to the left, the slope of the graph f is strictly negative which implies that the derivative graph
From the given graph, it is observed that the graph has high sharpness at origin. So, there is no unique tangent line at origin. Thus, the given graph is not differentiable at
From the point A to right, the slope of the graph f is strictly positive which implies that the derivative graph must have a functional value in positive.
Graph:
Use the above information and obtain the graph of
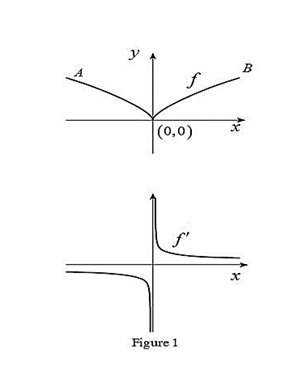
Thus,
Chapter 2 Solutions
Single Variable Calculus: Concepts and Contexts, Enhanced Edition
Additional Math Textbook Solutions
Calculus: Early Transcendentals (2nd Edition)
Calculus and Its Applications (11th Edition)
Calculus 2012 Student Edition (by Finney/Demana/Waits/Kennedy)
Precalculus
Precalculus: Concepts Through Functions, A Unit Circle Approach to Trigonometry (4th Edition)
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





