Chapter 3, Problem 26P

An airplane maintains a speed of 630 km/h relative to the air it is flying through, as it makes a trip to a city 750 km away to the north, (a) What time interval is required for the trip if the plane flies through a headwind blowing at 35.0 km/h toward the south? (b) What time interval is required if there is a tailwind with the same speed? (c) What time interval is required if there is a crosswind blowing at 35.0 km/h to the east relative to the ground?

To determine

The time interval for the trip if the plane flies trough a headwind blowing at $35.0\text{km/h}$ towards the south.

Answer to Problem 26P

The time interval for the trip is $1.26\text{h}$.

Explanation of Solution

Let positive $x$ axis be eastward and the positive $y$ axis be northward.

The displacement of the plane relative to the ground is,

$d_{\text{PG}}=750\text{km}$ due north.

The displacement of the plane relative to the air is,

$d_{\text{PA}}=\left(630\text{km/h}\right)t$ directed at angle $\alpha$ relative to the $y$ axis.

The displacement of the air relative to the ground is,

$d_{\text{AG}}=\left(35.0\text{km/h}\right)t$ directed at angle $\beta$ relative to the $y$ axis.

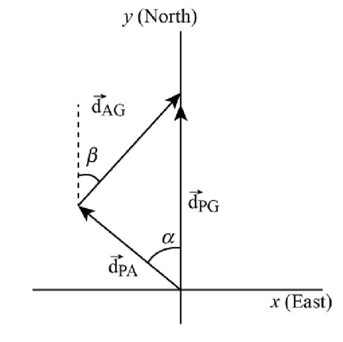
From the vector triangle, equating the $x$ components,

$-d_{\text{PA}}\sin \alpha +d_{\text{AG}}\sin \beta =0$

Here,

$\alpha$ is the angle between $d_{\text{PA}}$ and $d_{\text{AG}}$

$\beta$ is the angle between the normal and $d_{\text{AG}}$

Substitute $\left(630\text{km/h}\right)t$ for $d_{\text{PA}}$ and $\left(35.0\text{km/h}\right)t$ for $d_{\text{AG}}$.

$-\left(\left(630\text{km/h}\right)t\right)\sin \alpha +\left(\left(35.0\text{km/h}\right)t\right)\sin \beta =0$

$\sin \alpha =\frac{35.0}{630}\sin \beta$ (1)

Equating the $y$ components,

$d_{\text{PA}}\cos \alpha +d_{\text{AG}}\cos \beta =d_{\text{PG}}$

Substitute $\left(630\text{km/h}\right)t$ for $d_{\text{PA}}$, $\left(35.0\text{km/h}\right)t$ for $d_{\text{AG}}$ and $\left(750\text{km/h}\right)$ for $d_{\text{PG}}$.

$\left[\left(630\text{km/h}\right)\cos 3.18°+\left(35.0\text{km/h}\right)\cos \beta \right]t=750\text{km/h}$ (2)

The wind blows towards south ($\beta =180°$)and is a headwind for the plane ($\alpha =0°$).

Substituting $180°$ for $\beta$ and $0°$ for $\alpha$ in equation (II), we get

$\begin{array}{c}\left[\left(630\text{km/h}\right)\cos 0°+\left(35.0\text{km/h}\right)\cos 180°\right]t=750\text{km/h}\\ \left(630\text{km/h}-35.0\text{km/h}\right)t=750\text{km/h}\\ t=\frac{750\text{km/h}}{595\text{km/h}}\\ =1.26\text{h}\end{array}$

Conclusion:

Thus, the time interval for the trip is $1.26\text{h}$.

To determine

The time interval for the trip if the plane flies trough a tailwind blowing at $35.0\text{km/h}$.

Answer to Problem 26P

The time interval for the trip is $1.13\text{h}$.

Explanation of Solution

We have the second equation,

$\left[\left(630\text{km/h}\right)\cos 3.18°+\left(35.0\text{km/h}\right)\cos \beta \right]t=750\text{km/h}$

As the wind blows northward as a tailwind, substitute $0°$ for $\alpha$ and $\beta$.

$\begin{array}{c}\left[\left(630\text{km/h}\right)\cos 0°+\left(35.0\text{km/h}\right)\cos 0°\right]t=750\text{km/h}\\ \left[630\text{km/h}+35.0\text{km/h}\right]t=750\text{km/h}\\ t=\frac{750\text{km/h}}{665\text{km/h}}\\ =1.13\text{h}\end{array}$

Conclusion:

The time interval for the trip is $1.13\text{h}$.

To determine

The time interval for the trip if the plane flies trough a crosswind blowing at $35.0\text{km/h}$ towards the east relative to the ground.

Answer to Problem 26P

The time interval for the trip is $1.19\text{h}$.

Explanation of Solution

We have the first equation,

$\sin \alpha =\frac{35.0}{630}\sin \beta$

As the wind blows east, substitute $90.0°$ for $\beta$.

$\begin{array}{c}\sin \alpha =\frac{35.0}{630}\sin 90.0°\\ =0.056\\ \alpha ={\sin }^{-1}\left(0.056\right)\\ =3.18°\end{array}$

That is, the plane must fly $3.18°$ west of north relative to the air to maintain a due north heading relative to the ground.

 We have the second equation,

$\left[\left(630\text{km/h}\right)\cos 3.18°+\left(35.0\text{km/h}\right)\cos \beta \right]t=750\text{km/h}$

Substitute $90.0°$ for $\beta$ and $3.18°$ for $\alpha$.

$\begin{array}{c}\left[\left(630\text{km/h}\right)\cos 3.18°+\left(35.0\text{km/h}\right)\cos 90.0°\right]t=750\text{km/h}\\ t=\frac{750\text{km/h}}{626\text{km/h}+0}\\ =1.19\text{h}\end{array}$

Conclusion:

Thus, the time interval for the trip is $1.19\text{h}$.