College Physics
11th Edition
ISBN: 9781305952300
Author: Raymond A. Serway, Chris Vuille
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 3, Problem 48AP
When baseball outfielders throw the ball, they usually allow it to take one bounce, on the theory that the ball arrives at its target sooner that way. Suppose that, after the bounce, the ball rebounds at the same angle θ that it had when it was released (as in Fig. P3.48), but loses half its speed, (a) Assuming that the ball is always thrown with the same initial speed, at what angle θ should the ball be thrown in order to go the same distance D with one bounce as a ball thrown upward at 45.0° with no bounce? (b) Determine the ratio of the times for the one-bounce and no-bounce throws.
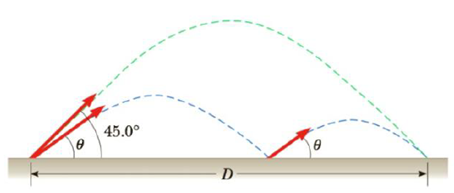
Figure P3.48
Expert Solution & Answer
Trending nowThis is a popular solution!
Students have asked these similar questions
In a volleyball game held in school, Player A at position X serves the ball from a height of 1.3m from the ground, imparting it with an initial velocity at an angle of 50 degrees from the horizontal, He aimed the all to land at point O, 0.5m short to Player B, thus making an ace, Incidentally the Player B is an expert in mind reading. The instant the server hits the ball, Player B started running from rest with a constant acceleration
a. Check whether the ball willclear the 2.42m high net.(answer in meters)b. At what horizontal distance in meters from position Y will Player B intercept the ball, given that he intercepts it at a height of 1.6m?c. What is the acceleration in m/s^2 of Player B
A pilot flies horizontally at 1300 km/h, at height h = 35 m above initially level ground. However, at time t = 0, the pilot begins to fly over ground sloping upward at angle u = 4.3°. If the pilot does not change the airplane’s heading, at what time t does the plane strike the ground?
A marble is launched from the edge of a table at a angle of 45 ° up from horizontal and goes through the air until it hits the floor. True or False? For such a marble, |vx| (the magnitude of the x-component of the velocity) is decreasing the entire time the marble is airborne.
Chapter 3 Solutions
College Physics
Ch. 3.1 - Which of the following objects cant be...Ch. 3.1 - Consider the following controls in an automobile:...Ch. 3.1 - A girl on a bicycle takes 15.0 s to ride half way...Ch. 3.1 - Suppose you are carrying a ball and running at...Ch. 3.1 - As a projectile moves in its parabolic path, where...Ch. 3 - As a projectile moves in its path, is there any...Ch. 3 - Construct motion diagrams showing the velocity and...Ch. 3 - Explain whether the following particles do or do...Ch. 3 - A ball is projected horizontally from the top of a...Ch. 3 - A projectile is launched with speed v0 at an angle...
Ch. 3 - Determine which of the following moving objects...Ch. 3 - Two projectiles are thrown with the same initial...Ch. 3 - A ball is thrown upward in the air by a passenger...Ch. 3 - A projectile is launched at some angle to the...Ch. 3 - A baseball is thrown from the outfield toward the...Ch. 3 - A student throws a heavy red ball horizontally...Ch. 3 - A boat is heading due east at speed v when...Ch. 3 - As an apple tree is transported by a truck moving...Ch. 3 - An airplane in a holding pattern flies at constant...Ch. 3 - A hiker walks 2.00 km north and then 3.00 km east,...Ch. 3 - A miniature quadcopter is located at xi = 2.00 m...Ch. 3 - An ant crawls on the floor along the curved path...Ch. 3 - Explain whether the following particles do or do...Ch. 3 - A rabbit is moving in the positive x-direction at...Ch. 3 - A student stands at the edge of a cliff and throws...Ch. 3 - One of the fastest recorded pitches in major...Ch. 3 - The best leaper in the animal kingdom is the puma,...Ch. 3 - A rock is thrown upward from the level ground in...Ch. 3 - A placekicker must kick a football from a point...Ch. 3 - The record distance in the sport of throwing...Ch. 3 - A brick is thrown upward from the top of a...Ch. 3 - From the window of a building, a ball is tossed...Ch. 3 - A car is parked on a cliff overlooking the ocean...Ch. 3 - An artillery shell is fired with an initial...Ch. 3 - A projectile is launched with an initial speed of...Ch. 3 - A fireman d = 50.0 m away from a burning building...Ch. 3 - A playground is on the flat roof of a city school,...Ch. 3 - A cruise ship sails due north at 4.50 m/s while a...Ch. 3 - Suppose a boat moves at 12.0 m/s relative to the...Ch. 3 - A car travels due east with a speed of 50.0 km/h....Ch. 3 - A jet airliner moving initially at 3.00 102 mi/h...Ch. 3 - A Coast Guard cutter detects an unidentified ship...Ch. 3 - A bolt drops from the ceiling of a moving train...Ch. 3 - An airplane maintains a speed of 630 km/h relative...Ch. 3 - Suppose a chinook salmon needs to jump a waterfall...Ch. 3 - An airplane maintains a speed of 630 km/h relative...Ch. 3 - A river has a steady speed of 0.500 m/s. A student...Ch. 3 - This is a symbolic version of Problem 29. A river...Ch. 3 - How long does it take ail automobile traveling in...Ch. 3 - A moving walkway at an airport has a speed v1 and...Ch. 3 - A boy throws a baseball onto a roof and it rolls...Ch. 3 - You can use any coordinate system you like to...Ch. 3 - Towns A and B in Figure P3.35 are 80.0 km apart. A...Ch. 3 - In a local diner, a customer slides an empty...Ch. 3 - A father demonstrates projectile motion to his...Ch. 3 - Two canoeists in identical canoes exert the same...Ch. 3 - A rocket is launched at an angle of 53.0 above the...Ch. 3 - A farm truck travels due east with a constant...Ch. 3 - (a) If a person can jump a maximum horizontal...Ch. 3 - A ball is thrown straight upward and returns to...Ch. 3 - A home run is hit in such a way that the baseball...Ch. 3 - A 2.00-m-tall basketball player is standing on the...Ch. 3 - A quarterback throws a football toward a receiver...Ch. 3 - The x- and y-coordinates of a projectile launched...Ch. 3 - Spitting cobras can defend themselves by squeezing...Ch. 3 - When baseball outfielders throw the ball, they...Ch. 3 - A hunter wishes to cross a river that is 1.5 km...Ch. 3 - Chinook salmon are able to move upstream faster by...Ch. 3 - A daredevil is shot out of a cannon at 45.0 to the...Ch. 3 - If raindrops are falling vertically at 7.50 m/s,...Ch. 3 - A celebrated Mark Twain story has motivated...Ch. 3 - A landscape architect is planning an artificial...Ch. 3 - A golf ball with an initial speed of 50.0 m/s...Ch. 3 - Antlion larvae lie in wait for prey at the bottom...Ch. 3 - One strategy in a snowball fight is to throw a...Ch. 3 - A football receiver running straight downfield at...Ch. 3 - The determined Wile E. Coyote is out once more to...
Additional Science Textbook Solutions
Find more solutions based on key concepts
Check Your Understanding The changes of momentum for Philae and for Comet 67/P were equal (in magnitude). Were ...
University Physics Volume 1
How is the charging time for a capacitor correlated with the initial current? That is, if the initial current i...
Matter and Interactions
Order of Magnitude Estimate. Mathematical Insight 1.3 defines order of magnitude estimates, and in the text we ...
The Cosmic Perspective (9th Edition)
Explain what happens to the energy carried by light that it is dimmed by passing it through two crossed polariz...
College Physics
GO You testify as an expert witness in a case involving an accident in which car A slid into the rear of car B,...
Fundamentals of Physics Extended
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, physics and related others by exploring similar questions and additional content below.Similar questions
- Consider a projectile launched form ground level at an angle of elevation with an initial velocity . The maximum horizontal range is given by xmax=(v 2/0 sin2θ)/g, where g is the acceleration due to gravity. Here is the problem: If a soccer ball is kicked from ground level with an initial velocity of 28 m/sec, what is the smallest positive angle at which the player should kick the ball to reach a teammate 48m down the field? Assume that the ball reaches the teammate at ground level on the fly. Round to the nearest tenth of a degree.arrow_forwardA rugby player runs with the ball directly toward his opponent’s goal, along the positive direction of an x axis. He can legally pass the ball to a teammate as long as the ball’s velocity relative to the field does not have a positive x component. Suppose the player runs at speed 4.0 m/s relative to the field while he passes the ball with velocity relative to himself. If has magnitude 6.0 m/s, what is the smallest angle it can have for the pass to be legal?arrow_forwardYou buy a plastic dart gun, and being a clever physics student you decide to do a quick calculation to find its maximum horizontal range. You shoot the gun straight up, and it takes 3.6 ss for the dart to land back at the barrel.arrow_forward
- Particle A moves along the line y = 30 m with a constant velocity vector v of magnitude 3.0 m/s and parallel to the x axis. At the instant particle A passes the y axis , particle B leaves the origin with a zero initial speed and a constant acceleration vector a of magnitude 0.40 m/s2 . What angle theta between vector a and the positive direction of the y axis would result in a collision?arrow_forwardA projectile is launched with a launch angle of 30° with respect to the horizontal direction and with an initial speed of 26 m/s. How do the vertical and horizontal components of the projectile's velocity vary with time?The initial velocity in the x-direction vx0 is related to the initial speed by vx0 = v0 cos 30°. The constant velocity in the x-direction means that the equation describing the time dependence of x for the particle, with x0 taken as 0, is x = x0 + vx0t = 0 + m/s t. The equation for the vertical coordinate, which is constantly accelerating downward at g = 9.8 m/s2, is y = y0 + vy0t − 1 2 gt2 = m/s t + m/s2 t2.arrow_forwardparticle A moves along the line y 30 m with a constant velocity of magnitude 3.0 m/s and parallel to the x axis. At the instant particle A passes the y axis, particle B leaves the origin with a zero initial speed and a constant acceleration of magnitude 0.40 m/s2.What angle u between and the positive direction of the y axis would result in a collision?arrow_forward
- A punter kicks a football at an angle of 30 degrees with the horizontal at an initial speed of 15 m/s. Where should a punt returner position himself to catch the ball just before it strikes the ground?arrow_forwardAn inflatable life raft is released from an airplane at 300 m altitude, in level flight, with an air speed of 100 m/s in the horizontal direction. At what horizontal distance from the release point does the raft strike the water?arrow_forwardA stone is thrown horizontally from the highest point of a 95 m building and lands 115 m from the base of the building. Ignore air resistance, and use a coordinate system whose origin is at the highest point of the building, with positive y upwards and positive x in the direction of the throw. How long is the stone in the air in seconds? What must have been the initial horizontal component of the velocity, in meters per second? What is the vertical component of the velocity just before the stone hits the ground, in meters per second? What is the magnitude of the velocity of the stone just before it hits the ground, in meters per second?arrow_forward
- A rail gun shoots a projectile in a straight line with acceleration aa and in time tt as defined by the equation a(t)=3−2t. If the projectile from the launcher reaches a velocity of 10 at t=1 and if s(t) is the distance of the projectile from the rail gun at time t, find s(5)−s(1)arrow_forwardA snowball is thrown from ground level (by someone in a hole) with initial speed v0 at an angle of 45° relative to the (level) ground, on which the snowball later lands. If the launch angle is increased, do (a) the range and (b) the flight time increase, decrease, or stay the same?arrow_forwardA firefighter, a distance d from a burning building, directs a stream of water from a fire hose at angle i above the horizontal as shown in Figure P3.16. If the initial speed of the stream is vi, at what height h does the water strike the building? Figure P3.16arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University
Principles of Physics: A Calculus-Based Text
Physics
ISBN:9781133104261
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
University Physics Volume 1
Physics
ISBN:9781938168277
Author:William Moebs, Samuel J. Ling, Jeff Sanny
Publisher:OpenStax - Rice University
Kinematics Part 3: Projectile Motion; Author: Professor Dave explains;https://www.youtube.com/watch?v=aY8z2qO44WA;License: Standard YouTube License, CC-BY