
Single Variable Calculus: Early Transcendentals, Volume I
8th Edition
ISBN: 9781305270343
Author: James Stewart
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Textbook Question
Chapter 3.2, Problem 49E
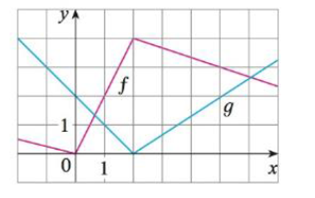
If f and g are the functions whose graphs are shown, let u(x) = f(x)g(x) and v(x) = f(x)/g(x).
(a) Find u'(l).
(b) Find v'(5).
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
find the derivative of y=(x-1)(2x-x2)1/2 - arccos(x-1)
Two equivalent forms of the Chain Rule for calculating the derivative of y = ƒ(g(x)) are presented in this section. State both forms.
Compute the derivative for y= (e^-4x sin^2(x)) / (x^2 + 3x + 1)
Chapter 3 Solutions
Single Variable Calculus: Early Transcendentals, Volume I
Ch. 3.1 - (a) How is the number e defined? (b) Use a...Ch. 3.1 - (a) Sketch, by hand, the graph of the function...Ch. 3.1 - Differentiate the function. f(x) = 240Ch. 3.1 - Prob. 4ECh. 3.1 - Differentiate the function. f(x) = 5.2x + 2.3Ch. 3.1 - Prob. 6ECh. 3.1 - Prob. 7ECh. 3.1 - Differentiate the function. f(t) = 1.4t5 2.5t2+...Ch. 3.1 - Prob. 9ECh. 3.1 - Differentiate the function. H(u) = (3u 1)(u + 2)
Ch. 3.1 - Prob. 11ECh. 3.1 - Prob. 12ECh. 3.1 - Prob. 13ECh. 3.1 - Prob. 14ECh. 3.1 - Prob. 15ECh. 3.1 - Prob. 16ECh. 3.1 - Prob. 17ECh. 3.1 - Prob. 18ECh. 3.1 - Prob. 19ECh. 3.1 - Differentiate the function. S(R) = 4R2Ch. 3.1 - Prob. 21ECh. 3.1 - Prob. 22ECh. 3.1 - Prob. 23ECh. 3.1 - Prob. 24ECh. 3.1 - Prob. 25ECh. 3.1 - Differentiate the function. k(r) = er + reCh. 3.1 - Prob. 27ECh. 3.1 - Prob. 28ECh. 3.1 - Prob. 29ECh. 3.1 - Prob. 30ECh. 3.1 - Prob. 31ECh. 3.1 - Prob. 32ECh. 3.1 - Find an equation of the tangent line to the curve...Ch. 3.1 - Prob. 34ECh. 3.1 - Prob. 35ECh. 3.1 - Prob. 36ECh. 3.1 - Find equations of the tangent line and normal line...Ch. 3.1 - Prob. 38ECh. 3.1 - Prob. 39ECh. 3.1 - Prob. 40ECh. 3.1 - Prob. 41ECh. 3.1 - Prob. 42ECh. 3.1 - Prob. 43ECh. 3.1 - Prob. 44ECh. 3.1 - Find the first and second derivatives of the...Ch. 3.1 - Prob. 46ECh. 3.1 - Prob. 47ECh. 3.1 - Prob. 48ECh. 3.1 - The equation of motion of a particle is s = t3 ...Ch. 3.1 - The equation of motion of a particle is s = t4 ...Ch. 3.1 - Prob. 51ECh. 3.1 - The number of tree species S in a given area A in...Ch. 3.1 - Prob. 53ECh. 3.1 - Prob. 55ECh. 3.1 - Prob. 56ECh. 3.1 - Show that the curve y = 2ex + 3x + 5x3 has no...Ch. 3.1 - Prob. 58ECh. 3.1 - Prob. 59ECh. 3.1 - Prob. 60ECh. 3.1 - Prob. 61ECh. 3.1 - Prob. 62ECh. 3.1 - Prob. 63ECh. 3.1 - Prob. 64ECh. 3.1 - Prob. 65ECh. 3.1 - Find the nth derivative of each function by...Ch. 3.1 - Prob. 67ECh. 3.1 - Prob. 68ECh. 3.1 - Find a cubic function y = ax3 + bx2 + cx + d whose...Ch. 3.1 - Prob. 70ECh. 3.1 - Prob. 71ECh. 3.1 - Prob. 72ECh. 3.1 - Prob. 73ECh. 3.1 - Prob. 74ECh. 3.1 - Prob. 75ECh. 3.1 - Suppose the curve y = x4 + ax3 + bx2 + cx + d has...Ch. 3.1 - Prob. 77ECh. 3.1 - Prob. 78ECh. 3.1 - Prob. 79ECh. 3.1 - Prob. 80ECh. 3.1 - Prob. 81ECh. 3.1 - A tangent line is drawn to the hyperbola xy = c at...Ch. 3.1 - Evaluate limx1x10001x1.Ch. 3.1 - Prob. 84ECh. 3.1 - Prob. 85ECh. 3.1 - Prob. 86ECh. 3.2 - Prob. 1ECh. 3.2 - Prob. 2ECh. 3.2 - Prob. 3ECh. 3.2 - Prob. 4ECh. 3.2 - Prob. 5ECh. 3.2 - Prob. 6ECh. 3.2 - Prob. 7ECh. 3.2 - Prob. 8ECh. 3.2 - Prob. 9ECh. 3.2 - Prob. 10ECh. 3.2 - Prob. 11ECh. 3.2 - Prob. 12ECh. 3.2 - Prob. 13ECh. 3.2 - Prob. 14ECh. 3.2 - Differentiate. y=t3+3tt24t+3Ch. 3.2 - Prob. 16ECh. 3.2 - Differentiate. y=ep(p+pp)Ch. 3.2 - Prob. 18ECh. 3.2 - Prob. 19ECh. 3.2 - Prob. 20ECh. 3.2 - Prob. 21ECh. 3.2 - Prob. 22ECh. 3.2 - Prob. 23ECh. 3.2 - Prob. 24ECh. 3.2 - Differentiate. f(x)=xx+cxCh. 3.2 - Prob. 26ECh. 3.2 - Find f'(x) and f"(x). f(x) = (x3 + 1)exCh. 3.2 - Prob. 28ECh. 3.2 - Prob. 29ECh. 3.2 - Prob. 30ECh. 3.2 - Prob. 31ECh. 3.2 - Prob. 32ECh. 3.2 - Prob. 33ECh. 3.2 - Prob. 34ECh. 3.2 - (a) The curve y = 1/(1 + x2) is called a witch of...Ch. 3.2 - Prob. 36ECh. 3.2 - Prob. 37ECh. 3.2 - Prob. 38ECh. 3.2 - Prob. 39ECh. 3.2 - Prob. 40ECh. 3.2 - Prob. 41ECh. 3.2 - Prob. 42ECh. 3.2 - Prob. 43ECh. 3.2 - Suppose that f(4) = 2, g(4) = 5, f'(4) = 6. and...Ch. 3.2 - If f(x) = exg(x), where g(0) = 2 and g'(0) = 5,...Ch. 3.2 - If h(2) = 4 and h'(2) = 3, find ddx(h(x)x)|x=2Ch. 3.2 - Prob. 47ECh. 3.2 - Prob. 48ECh. 3.2 - If f and g are the functions whose graphs are...Ch. 3.2 - Prob. 50ECh. 3.2 - Prob. 51ECh. 3.2 - Prob. 52ECh. 3.2 - How many tangent lines to the curve y = x/(x + 1)...Ch. 3.2 - Prob. 54ECh. 3.2 - Prob. 55ECh. 3.2 - Prob. 56ECh. 3.2 - In this exercise we estimate the rate at which the...Ch. 3.2 - A manufacturer produces bolts of a fabric with a...Ch. 3.2 - Prob. 59ECh. 3.2 - The biomass B(t) of a fish population is the total...Ch. 3.2 - (a) Use the Product Rule twice to prove that if f,...Ch. 3.2 - Prob. 62ECh. 3.2 - Prob. 63ECh. 3.2 - Prob. 64ECh. 3.3 - Differentiate. f(x) = x2 sin xCh. 3.3 - Prob. 2ECh. 3.3 - Prob. 3ECh. 3.3 - Prob. 4ECh. 3.3 - Differentiate. y = sec tanCh. 3.3 - Prob. 6ECh. 3.3 - Differentiate. y = c cos t + t2 sin tCh. 3.3 - Differentiate. f(t)=cottetCh. 3.3 - Prob. 9ECh. 3.3 - Prob. 10ECh. 3.3 - Prob. 11ECh. 3.3 - Prob. 12ECh. 3.3 - Prob. 13ECh. 3.3 - Prob. 14ECh. 3.3 - Prob. 15ECh. 3.3 - Differentiate. f(t) = tet cot tCh. 3.3 - Prove that ddx(cscx)=cscxcotx.Ch. 3.3 - Prob. 18ECh. 3.3 - Prob. 19ECh. 3.3 - Prob. 20ECh. 3.3 - Prob. 21ECh. 3.3 - Prob. 22ECh. 3.3 - Prob. 23ECh. 3.3 - Prob. 24ECh. 3.3 - Prob. 25ECh. 3.3 - Prob. 26ECh. 3.3 - Prob. 27ECh. 3.3 - Prob. 28ECh. 3.3 - Prob. 29ECh. 3.3 - Prob. 30ECh. 3.3 - Prob. 31ECh. 3.3 - Prob. 32ECh. 3.3 - Prob. 33ECh. 3.3 - For what values of x does the graph of f have a...Ch. 3.3 - Prob. 35ECh. 3.3 - Prob. 36ECh. 3.3 - A ladder 10 ft long rests against a vertical wall....Ch. 3.3 - Prob. 38ECh. 3.3 - Prob. 39ECh. 3.3 - Prob. 40ECh. 3.3 - Prob. 41ECh. 3.3 - Prob. 42ECh. 3.3 - Prob. 43ECh. 3.3 - Find the limit. limx0sin3xsin5xx2Ch. 3.3 - Prob. 45ECh. 3.3 - Prob. 46ECh. 3.3 - Prob. 47ECh. 3.3 - Find the limit. limx0sin(x2)xCh. 3.3 - Prob. 49ECh. 3.3 - Prob. 50ECh. 3.3 - Find the given derivative by finding the first few...Ch. 3.3 - Find the given derivative by finding the first few...Ch. 3.3 - Prob. 53ECh. 3.3 - Prob. 54ECh. 3.3 - Prob. 55ECh. 3.3 - A semicircle with diameter PQ sits on an isosceles...Ch. 3.3 - Prob. 57ECh. 3.3 - Prob. 58ECh. 3.4 - Write the composite function in the form f(g(x))....Ch. 3.4 - Prob. 2ECh. 3.4 - Write the composite function in the form f(g(x))....Ch. 3.4 - Prob. 4ECh. 3.4 - Prob. 5ECh. 3.4 - Prob. 6ECh. 3.4 - Prob. 7ECh. 3.4 - Prob. 8ECh. 3.4 - Prob. 9ECh. 3.4 - Prob. 10ECh. 3.4 - Prob. 11ECh. 3.4 - Prob. 12ECh. 3.4 - Prob. 13ECh. 3.4 - Prob. 14ECh. 3.4 - Prob. 15ECh. 3.4 - Prob. 16ECh. 3.4 - Prob. 17ECh. 3.4 - Prob. 18ECh. 3.4 - Prob. 19ECh. 3.4 - Prob. 20ECh. 3.4 - Prob. 21ECh. 3.4 - Prob. 22ECh. 3.4 - Find the derivative of the function. y = e tanCh. 3.4 - Prob. 24ECh. 3.4 - Prob. 25ECh. 3.4 - Prob. 26ECh. 3.4 - Prob. 27ECh. 3.4 - Find the derivative of the function. f(z) =...Ch. 3.4 - Prob. 29ECh. 3.4 - Prob. 30ECh. 3.4 - Prob. 31ECh. 3.4 - Prob. 32ECh. 3.4 - Prob. 33ECh. 3.4 - Prob. 34ECh. 3.4 - Prob. 35ECh. 3.4 - Prob. 36ECh. 3.4 - Prob. 37ECh. 3.4 - Prob. 38ECh. 3.4 - Prob. 39ECh. 3.4 - Prob. 40ECh. 3.4 - Prob. 41ECh. 3.4 - Prob. 42ECh. 3.4 - Prob. 43ECh. 3.4 - Prob. 44ECh. 3.4 - Prob. 45ECh. 3.4 - Prob. 46ECh. 3.4 - Prob. 47ECh. 3.4 - Prob. 48ECh. 3.4 - Prob. 49ECh. 3.4 - Prob. 50ECh. 3.4 - Prob. 51ECh. 3.4 - Prob. 52ECh. 3.4 - Prob. 53ECh. 3.4 - Prob. 54ECh. 3.4 - Prob. 55ECh. 3.4 - Prob. 56ECh. 3.4 - Prob. 57ECh. 3.4 - Prob. 58ECh. 3.4 - Prob. 59ECh. 3.4 - Prob. 60ECh. 3.4 - Prob. 61ECh. 3.4 - Prob. 62ECh. 3.4 - Prob. 63ECh. 3.4 - Prob. 64ECh. 3.4 - If f and g are the functions whose graphs are...Ch. 3.4 - Prob. 66ECh. 3.4 - Prob. 67ECh. 3.4 - Prob. 68ECh. 3.4 - Prob. 69ECh. 3.4 - Prob. 70ECh. 3.4 - Prob. 71ECh. 3.4 - Prob. 72ECh. 3.4 - Prob. 73ECh. 3.4 - Prob. 74ECh. 3.4 - Prob. 75ECh. 3.4 - Prob. 76ECh. 3.4 - Prob. 77ECh. 3.4 - Find the 1000th derivative of f(x) = xex.Ch. 3.4 - Prob. 79ECh. 3.4 - Prob. 80ECh. 3.4 - A Cepheid variable star is a star whose brightness...Ch. 3.4 - Prob. 82ECh. 3.4 - Prob. 83ECh. 3.4 - Prob. 84ECh. 3.4 - Prob. 85ECh. 3.4 - Prob. 86ECh. 3.4 - A particle moves along a straight line with...Ch. 3.4 - Prob. 88ECh. 3.4 - The flash unit on a camera operates by storing...Ch. 3.4 - Prob. 90ECh. 3.4 - Use the Chain Rule to prove the following. (a) The...Ch. 3.4 - Prob. 94ECh. 3.4 - Prob. 95ECh. 3.4 - Prob. 96ECh. 3.4 - Prob. 97ECh. 3.4 - Prob. 98ECh. 3.4 - Prob. 99ECh. 3.4 - Prob. 100ECh. 3.5 - (a) Find y by implicit differentiation. (b) Solve...Ch. 3.5 - Prob. 2ECh. 3.5 - Prob. 3ECh. 3.5 - Prob. 4ECh. 3.5 - Prob. 5ECh. 3.5 - Prob. 6ECh. 3.5 - Prob. 7ECh. 3.5 - Prob. 8ECh. 3.5 - Prob. 9ECh. 3.5 - Prob. 10ECh. 3.5 - Find dy/dx by implicit differentiation. 11. y cos...Ch. 3.5 - Prob. 12ECh. 3.5 - Prob. 13ECh. 3.5 - Prob. 14ECh. 3.5 - Prob. 15ECh. 3.5 - Prob. 16ECh. 3.5 - Prob. 17ECh. 3.5 - Prob. 18ECh. 3.5 - Prob. 19ECh. 3.5 - Prob. 20ECh. 3.5 - Prob. 21ECh. 3.5 - Prob. 22ECh. 3.5 - Prob. 23ECh. 3.5 - Regard y as the independent variable and x as the...Ch. 3.5 - Prob. 25ECh. 3.5 - Use implicit differentiation to find an equation...Ch. 3.5 - Prob. 27ECh. 3.5 - Prob. 28ECh. 3.5 - Prob. 29ECh. 3.5 - Prob. 30ECh. 3.5 - Prob. 31ECh. 3.5 - Prob. 32ECh. 3.5 - (a) The curve with equation y2 = 5x4 x2 is called...Ch. 3.5 - (a) The curve with equation y2 = x3 + 3x2 is...Ch. 3.5 - Prob. 35ECh. 3.5 - Prob. 36ECh. 3.5 - Prob. 37ECh. 3.5 - Prob. 38ECh. 3.5 - Prob. 39ECh. 3.5 - If x2 + xy + y3 = 1, find the value of y at the...Ch. 3.5 - Prob. 43ECh. 3.5 - Show by implicit differentiation that the tangent...Ch. 3.5 - Prob. 45ECh. 3.5 - Prob. 46ECh. 3.5 - Show, using implicit differentiation, that any...Ch. 3.5 - Prob. 48ECh. 3.5 - Prob. 49ECh. 3.5 - Prob. 50ECh. 3.5 - Prob. 51ECh. 3.5 - Prob. 52ECh. 3.5 - Prob. 53ECh. 3.5 - Prob. 54ECh. 3.5 - Prob. 55ECh. 3.5 - Prob. 56ECh. 3.5 - Prob. 57ECh. 3.5 - Prob. 58ECh. 3.5 - Prob. 59ECh. 3.5 - Prob. 60ECh. 3.5 - Prob. 61ECh. 3.5 - Prob. 62ECh. 3.5 - Prob. 63ECh. 3.5 - Prob. 64ECh. 3.5 - Prob. 65ECh. 3.5 - Prob. 66ECh. 3.5 - Prob. 67ECh. 3.5 - Prob. 68ECh. 3.5 - Show that the ellipse x2/a2 + y2/b2 = 1 and the...Ch. 3.5 - Prob. 70ECh. 3.5 - Prob. 71ECh. 3.5 - The equation x2 xy + y2 = 3 re presents a...Ch. 3.5 - Prob. 74ECh. 3.5 - Prob. 75ECh. 3.5 - Prob. 76ECh. 3.5 - (a) Suppose f is a one-to-one differentiable...Ch. 3.5 - Prob. 78ECh. 3.5 - The Bessel function of order 0, y = J(x),...Ch. 3.5 - Prob. 80ECh. 3.6 - Explain why the natural logarithmic function y =...Ch. 3.6 - Prob. 2ECh. 3.6 - Prob. 3ECh. 3.6 - Differentiate the function. f(x) = ln(sin2x)Ch. 3.6 - Differentiate the function. f(x)=ln1xCh. 3.6 - Prob. 6ECh. 3.6 - Differentiate the function. f(x) = log10(1 + cos...Ch. 3.6 - Prob. 8ECh. 3.6 - Prob. 9ECh. 3.6 - Prob. 10ECh. 3.6 - Prob. 11ECh. 3.6 - Prob. 12ECh. 3.6 - Prob. 13ECh. 3.6 - Prob. 14ECh. 3.6 - Prob. 15ECh. 3.6 - Prob. 16ECh. 3.6 - Differentiate the function. T(z) = 2z log2zCh. 3.6 - Differentiate the function. y = ln(csc x cot x)Ch. 3.6 - Differentiate the function. y = ln(ex + xex)Ch. 3.6 - Prob. 20ECh. 3.6 - Differentiate the function. y = tan[ln(ax + b)]Ch. 3.6 - Differentiate the function. y = log2 (x log5 x)Ch. 3.6 - Prob. 23ECh. 3.6 - Prob. 24ECh. 3.6 - Prob. 25ECh. 3.6 - Prob. 26ECh. 3.6 - Prob. 27ECh. 3.6 - Prob. 28ECh. 3.6 - Prob. 29ECh. 3.6 - Prob. 30ECh. 3.6 - Prob. 31ECh. 3.6 - Prob. 32ECh. 3.6 - Prob. 33ECh. 3.6 - Find an equation of the tangent line to the curve...Ch. 3.6 - If f(x) = sin x + ln x, find f(x). Check that your...Ch. 3.6 - Prob. 36ECh. 3.6 - Prob. 37ECh. 3.6 - Let f(x) = logb (3x2 2). For what value of b is...Ch. 3.6 - Prob. 39ECh. 3.6 - Prob. 40ECh. 3.6 - Prob. 41ECh. 3.6 - Prob. 42ECh. 3.6 - Prob. 43ECh. 3.6 - Prob. 44ECh. 3.6 - Prob. 45ECh. 3.6 - Prob. 46ECh. 3.6 - Use logarithmic differentiation to find the...Ch. 3.6 - Prob. 48ECh. 3.6 - Use logarithmic differentiation to find the...Ch. 3.6 - Prob. 50ECh. 3.6 - Prob. 51ECh. 3.6 - Prob. 52ECh. 3.6 - Prob. 53ECh. 3.6 - Prob. 54ECh. 3.6 - Prob. 55ECh. 3.6 - Prob. 56ECh. 3.7 - A particle moves according to a law of motion s =...Ch. 3.7 - A particle moves according to a law of motion s =...Ch. 3.7 - A particle moves according to a law of motion s =...Ch. 3.7 - Prob. 4ECh. 3.7 - Graphs of the velocity functions of two particles...Ch. 3.7 - Graphs of the position functions of two particles...Ch. 3.7 - The height (in meters) of a projectile shot...Ch. 3.7 - Prob. 8ECh. 3.7 - Prob. 9ECh. 3.7 - Prob. 10ECh. 3.7 - Prob. 11ECh. 3.7 - Prob. 12ECh. 3.7 - Prob. 13ECh. 3.7 - A stone is dropped into a lake, creating a...Ch. 3.7 - A spherical balloon is being inflated. Find the...Ch. 3.7 - Prob. 16ECh. 3.7 - The mass of the part of a metal rod that lies...Ch. 3.7 - If a tank holds 5000 gallons of water, which...Ch. 3.7 - Prob. 19ECh. 3.7 - Prob. 20ECh. 3.7 - Prob. 21ECh. 3.7 - Prob. 22ECh. 3.7 - Boyles Law states that when a sample of gas is...Ch. 3.7 - If, in Example 4, one molecule of the product C is...Ch. 3.7 - Prob. 25ECh. 3.7 - The number of yeast cells in a laboratory culture...Ch. 3.7 - The table shows how the average age of first...Ch. 3.7 - Refer to the law of laminar flow given in Example...Ch. 3.7 - Prob. 30ECh. 3.7 - Prob. 31ECh. 3.7 - Prob. 32ECh. 3.7 - If p(x) is the total value of the production when...Ch. 3.7 - Prob. 34ECh. 3.7 - Prob. 35ECh. 3.7 - Prob. 36ECh. 3.7 - Prob. 37ECh. 3.7 - Prob. 38ECh. 3.7 - In the study of ecosystems, predator-prey models...Ch. 3.8 - A population of protozoa develops with a constant...Ch. 3.8 - A common inhabitant of human intestines is the...Ch. 3.8 - A bacteria culture initially contains 100 cells...Ch. 3.8 - A bacteria culture grows with constant relative...Ch. 3.8 - Prob. 5ECh. 3.8 - Prob. 6ECh. 3.8 - Prob. 7ECh. 3.8 - Strontium-90 has a half-life of 28 days. (a) A...Ch. 3.8 - The half-life of cesium-137 is 30 years. Suppose...Ch. 3.8 - Prob. 10ECh. 3.8 - Scientists can determine the age of ancient...Ch. 3.8 - Dinosaur fossils are too old to be reliably dated...Ch. 3.8 - Prob. 13ECh. 3.8 - Prob. 14ECh. 3.8 - Prob. 15ECh. 3.8 - Prob. 16ECh. 3.8 - Prob. 17ECh. 3.8 - Prob. 18ECh. 3.8 - Prob. 19ECh. 3.8 - (a) If 1000 is borrowed at 8% interest, find the...Ch. 3.8 - (a) If 3000 is invested at 5% interest, find the...Ch. 3.8 - Prob. 22ECh. 3.9 - Prob. 1ECh. 3.9 - (a) If A is the area of a circle with radius r and...Ch. 3.9 - Each side of a square is increasing at a rate of 6...Ch. 3.9 - The length of a rectangle is increasing at a rate...Ch. 3.9 - Prob. 5ECh. 3.9 - The radius of a sphere is increasing at a rate of...Ch. 3.9 - Prob. 7ECh. 3.9 - The area of a triangle with sides of lengths a and...Ch. 3.9 - Prob. 9ECh. 3.9 - Suppose 4x2 + 9y2 = 36, where x and y are...Ch. 3.9 - Prob. 11ECh. 3.9 - Prob. 12ECh. 3.9 - Prob. 13ECh. 3.9 - Prob. 14ECh. 3.9 - Prob. 15ECh. 3.9 - Prob. 16ECh. 3.9 - Prob. 17ECh. 3.9 - A spotlight on the ground shines on a wall 12m...Ch. 3.9 - Prob. 19ECh. 3.9 - Prob. 20ECh. 3.9 - Prob. 21ECh. 3.9 - Prob. 22ECh. 3.9 - Prob. 23ECh. 3.9 - Prob. 24ECh. 3.9 - Prob. 25ECh. 3.9 - Prob. 26ECh. 3.9 - A water trough is 10m long and a cross-section has...Ch. 3.9 - A swimming pool is 20 ft wide, 40 ft long, 3 ft...Ch. 3.9 - Prob. 29ECh. 3.9 - A kite 100ft above the ground moves horizontally...Ch. 3.9 - Prob. 31ECh. 3.9 - Prob. 32ECh. 3.9 - Prob. 33ECh. 3.9 - According to the model we used to solve Example 2,...Ch. 3.9 - Prob. 35ECh. 3.9 - Prob. 36ECh. 3.9 - Prob. 37ECh. 3.9 - When air expands adiabatically (without gaining or...Ch. 3.9 - Prob. 39ECh. 3.9 - Prob. 40ECh. 3.9 - Prob. 41ECh. 3.9 - Two carts, A and B, are connected by a rope 39 ft...Ch. 3.9 - A television camera is positioned 4000 ft from the...Ch. 3.9 - A lighthouse is located on a small island 3 km...Ch. 3.9 - Prob. 45ECh. 3.9 - Prob. 46ECh. 3.9 - Prob. 47ECh. 3.9 - Prob. 48ECh. 3.9 - A runner sprints around a circular track of radius...Ch. 3.9 - Prob. 50ECh. 3.10 - Prob. 1ECh. 3.10 - Prob. 2ECh. 3.10 - Find the linearization L(x) of the function at n....Ch. 3.10 - Prob. 4ECh. 3.10 - Find the linear approximation of the function...Ch. 3.10 - Find the linear approximation of the function...Ch. 3.10 - Verify the given linear approximation at a = 0....Ch. 3.10 - Verify the given linear approximation at a = 0....Ch. 3.10 - Verify the given linear approximation at a = 0....Ch. 3.10 - Verify the given linear approximation at a = 0....Ch. 3.10 - Find the differential of each function. 11. (a) y...Ch. 3.10 - Find the differential of each function. 12. (a)...Ch. 3.10 - Find the differential of each function. 13. (a)...Ch. 3.10 - Find the differential of each function. 14. (a) y...Ch. 3.10 - (a) Find the differential dy and (b) evaluate dy...Ch. 3.10 - (a) Find the differential dy and (b) evaluate dy...Ch. 3.10 - (a) Find the differential dy and (b) evaluate dy...Ch. 3.10 - (a) Find the differential dy and (b) evaluate dy...Ch. 3.10 - Compute y and dy for the given values of x and dx...Ch. 3.10 - Compute y and dy for the given values of x and dx...Ch. 3.10 - Compute y and dy for the given values of x and dx...Ch. 3.10 - Compute y and dy for the given values of x and dx...Ch. 3.10 - Use a linear approximation (or differentials) to...Ch. 3.10 - Use a linear approximation (or differentials) to...Ch. 3.10 - Use a linear approximation (or differentials) to...Ch. 3.10 - Use a linear approximation (or differentials) to...Ch. 3.10 - Use a linear approximation (or differentials) to...Ch. 3.10 - Prob. 28ECh. 3.10 - Explain, in terms of linear approximations or...Ch. 3.10 - Prob. 30ECh. 3.10 - Explain, in terms of linear approximations or...Ch. 3.10 - Prob. 32ECh. 3.10 - The edge of a cube was found to be 30 cm with a...Ch. 3.10 - The radius of a circular disk is given as 24 cm...Ch. 3.10 - Prob. 35ECh. 3.10 - Use differentials to estimate the amount of paint...Ch. 3.10 - Prob. 37ECh. 3.10 - Prob. 38ECh. 3.10 - If a current I passes through a resistor with...Ch. 3.10 - When blood flows along a blood vessel, the flux F...Ch. 3.10 - Prob. 41ECh. 3.10 - Prob. 42ECh. 3.10 - Suppose that the only information we have about a...Ch. 3.10 - Prob. 44ECh. 3.11 - Prob. 1ECh. 3.11 - Prob. 2ECh. 3.11 - Find the numerical value of each expression. 3....Ch. 3.11 - Prob. 4ECh. 3.11 - Prob. 5ECh. 3.11 - Prob. 6ECh. 3.11 - Prob. 7ECh. 3.11 - Prob. 8ECh. 3.11 - Prob. 9ECh. 3.11 - Prob. 10ECh. 3.11 - Prob. 11ECh. 3.11 - Prob. 12ECh. 3.11 - Prove the identity. 13. coth2x 1 = csch2xCh. 3.11 - Prob. 14ECh. 3.11 - Prob. 15ECh. 3.11 - Prob. 16ECh. 3.11 - Prob. 17ECh. 3.11 - Prob. 18ECh. 3.11 - Prob. 19ECh. 3.11 - Prob. 20ECh. 3.11 - Prob. 21ECh. 3.11 - Prob. 22ECh. 3.11 - Use the definitions of the hyperbolic functions to...Ch. 3.11 - Prob. 24ECh. 3.11 - Prob. 25ECh. 3.11 - Prob. 26ECh. 3.11 - Prob. 27ECh. 3.11 - Prob. 28ECh. 3.11 - Prob. 29ECh. 3.11 - Prob. 30ECh. 3.11 - Prob. 31ECh. 3.11 - Prob. 32ECh. 3.11 - Prob. 33ECh. 3.11 - Prob. 34ECh. 3.11 - Prob. 35ECh. 3.11 - Prob. 36ECh. 3.11 - Prob. 37ECh. 3.11 - Prob. 38ECh. 3.11 - Prob. 39ECh. 3.11 - Prob. 40ECh. 3.11 - Prob. 41ECh. 3.11 - Prob. 42ECh. 3.11 - Prob. 43ECh. 3.11 - Prob. 44ECh. 3.11 - Prob. 45ECh. 3.11 - Prob. 46ECh. 3.11 - Show that ddx arctan(tanh x) = sech 2x.Ch. 3.11 - Prob. 48ECh. 3.11 - Prob. 49ECh. 3.11 - A flexible cable always hangs in the shape of a...Ch. 3.11 - Prob. 51ECh. 3.11 - Prob. 52ECh. 3.11 - Prob. 53ECh. 3.11 - Prob. 54ECh. 3.11 - Prob. 55ECh. 3.11 - Prob. 56ECh. 3.11 - Prob. 57ECh. 3.11 - Prob. 58ECh. 3 - State each differentiation rule both in symbols...Ch. 3 - Prob. 2RCCCh. 3 - Prob. 3RCCCh. 3 - Prob. 4RCCCh. 3 - Give several examples of how the derivative can be...Ch. 3 - Prob. 6RCCCh. 3 - Prob. 7RCCCh. 3 - Prob. 1RQCh. 3 - Prob. 2RQCh. 3 - Determine whether the statement is true or false....Ch. 3 - Prob. 4RQCh. 3 - Prob. 5RQCh. 3 - Prob. 6RQCh. 3 - Determine whether the statement is true or false....Ch. 3 - Prob. 8RQCh. 3 - Prob. 9RQCh. 3 - Prob. 10RQCh. 3 - Prob. 11RQCh. 3 - Determine whether the statement is true or false....Ch. 3 - Prob. 13RQCh. 3 - Prob. 14RQCh. 3 - Determine whether the statement is true or false....Ch. 3 - Prob. 1RECh. 3 - Prob. 2RECh. 3 - Prob. 3RECh. 3 - Prob. 4RECh. 3 - Prob. 5RECh. 3 - Prob. 6RECh. 3 - Prob. 7RECh. 3 - Prob. 8RECh. 3 - Prob. 9RECh. 3 - Prob. 10RECh. 3 - Prob. 11RECh. 3 - Prob. 12RECh. 3 - Prob. 13RECh. 3 - Prob. 14RECh. 3 - Prob. 15RECh. 3 - Prob. 16RECh. 3 - Prob. 17RECh. 3 - Prob. 18RECh. 3 - Prob. 19RECh. 3 - Prob. 20RECh. 3 - Prob. 21RECh. 3 - Prob. 22RECh. 3 - Prob. 23RECh. 3 - Prob. 24RECh. 3 - Prob. 25RECh. 3 - Prob. 26RECh. 3 - Prob. 27RECh. 3 - Prob. 28RECh. 3 - Prob. 29RECh. 3 - Prob. 30RECh. 3 - Prob. 31RECh. 3 - Prob. 32RECh. 3 - Prob. 33RECh. 3 - Prob. 34RECh. 3 - Prob. 35RECh. 3 - Prob. 36RECh. 3 - Prob. 37RECh. 3 - Prob. 38RECh. 3 - Prob. 39RECh. 3 - Prob. 40RECh. 3 - Prob. 41RECh. 3 - Prob. 42RECh. 3 - Prob. 43RECh. 3 - Prob. 44RECh. 3 - Prob. 45RECh. 3 - Prob. 46RECh. 3 - Prob. 47RECh. 3 - Prob. 48RECh. 3 - Prob. 49RECh. 3 - Prob. 50RECh. 3 - Prob. 51RECh. 3 - Prob. 52RECh. 3 - Prob. 53RECh. 3 - Prob. 54RECh. 3 - Use mathematical induction (page 72) to show that...Ch. 3 - Prob. 56RECh. 3 - Prob. 57RECh. 3 - Prob. 58RECh. 3 - Prob. 59RECh. 3 - Prob. 60RECh. 3 - Prob. 61RECh. 3 - Prob. 62RECh. 3 - Prob. 63RECh. 3 - (a) If f(x) = 4x tan x, /2 x /2, find f and f....Ch. 3 - Prob. 65RECh. 3 - Prob. 66RECh. 3 - Prob. 67RECh. 3 - Prob. 68RECh. 3 - Prob. 69RECh. 3 - If f and g are the functions whose graphs are...Ch. 3 - Prob. 71RECh. 3 - Prob. 72RECh. 3 - Prob. 73RECh. 3 - Prob. 74RECh. 3 - Prob. 75RECh. 3 - Prob. 76RECh. 3 - Prob. 77RECh. 3 - Prob. 78RECh. 3 - Prob. 79RECh. 3 - Prob. 80RECh. 3 - Prob. 81RECh. 3 - Prob. 82RECh. 3 - Prob. 83RECh. 3 - Prob. 84RECh. 3 - Find a parabola y = ax2 + bx + c that passes...Ch. 3 - Prob. 86RECh. 3 - Prob. 87RECh. 3 - Prob. 88RECh. 3 - A particle moves on a vertical line so that its...Ch. 3 - The volume of a right circular cone is V=13r2h,...Ch. 3 - Prob. 91RECh. 3 - Prob. 92RECh. 3 - Prob. 93RECh. 3 - Prob. 94RECh. 3 - Prob. 95RECh. 3 - Prob. 96RECh. 3 - Prob. 97RECh. 3 - Prob. 98RECh. 3 - A balloon is rising at a constant speed of 5 ft/s....Ch. 3 - Prob. 100RECh. 3 - The angle of elevation of the sun is decreasing at...Ch. 3 - Prob. 102RECh. 3 - Prob. 103RECh. 3 - Prob. 104RECh. 3 - Prob. 105RECh. 3 - Prob. 106RECh. 3 - Express the limit as a derivative and evaluate....Ch. 3 - Prob. 108RECh. 3 - Prob. 109RECh. 3 - Prob. 110RECh. 3 - Prob. 111RECh. 3 - Show that the length of the portion of any tangent...Ch. 3 - Prob. 1PCh. 3 - Prob. 2PCh. 3 - Prob. 3PCh. 3 - Prob. 4PCh. 3 - Prob. 5PCh. 3 - Find the values of the constants a and b such that...Ch. 3 - Show that sin-1(tanh x) = tan1(sinh x).Ch. 3 - A car is traveling at night along a highway shaped...Ch. 3 - Prob. 9PCh. 3 - Prob. 10PCh. 3 - Prob. 11PCh. 3 - Find all values of r such that the parabolas y =...Ch. 3 - Prob. 13PCh. 3 - Prob. 14PCh. 3 - The figure shows a rotating wheel with radius 40...Ch. 3 - Prob. 16PCh. 3 - Prob. 17PCh. 3 - Prob. 18PCh. 3 - Prob. 19PCh. 3 - Prob. 20PCh. 3 - Prob. 21PCh. 3 - Let P(x1, y1) be a point on the parabola y2 = 4px...Ch. 3 - Prob. 23PCh. 3 - Prob. 24PCh. 3 - Prob. 25PCh. 3 - Prob. 27PCh. 3 - Prob. 28PCh. 3 - Prob. 29PCh. 3 - Prob. 30PCh. 3 - Find the two points on the curve y = x4 2x2 x...Ch. 3 - Prob. 32PCh. 3 - A lattice point in the plane is a point with...Ch. 3 - Prob. 34PCh. 3 - Prob. 35P
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- 1) Calculate the derivative of f1 (x) = (2x + 3) / (x - 5) using the definition of the limit of the rate of variation. 2) Calculate the derivatives of the following functionsarrow_forwardFind a function y=f(x) whose second derivative is y''=12x-2 at each point (x,y) on its graph y=-x+5 and is tangent to the graph at the point corresponding to x=-1 .arrow_forwardFind the first derivative of y= 1/(1-x^4)^6 using the Chain Rule.arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning

Calculus: Early Transcendentals
Calculus
ISBN:9781285741550
Author:James Stewart
Publisher:Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:9780134438986
Author:Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:9780134763644
Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:9781319050740
Author:Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:W. H. Freeman


Calculus: Early Transcendental Functions
Calculus
ISBN:9781337552516
Author:Ron Larson, Bruce H. Edwards
Publisher:Cengage Learning
Derivatives of Trigonometric Functions - Product Rule Quotient & Chain Rule - Calculus Tutorial; Author: The Organic Chemistry Tutor;https://www.youtube.com/watch?v=_niP0JaOgHY;License: Standard YouTube License, CC-BY