Chapter 3.3, Problem 36E

An elastic band is hung on a hook and a mass is hung on the lower end of the band. When the mass is pulled downward and then released, it vibrates vertically. The equation of motion is s = 2 cos t + 3 sin t, t ≥ 0, where s is measured in centimeters and t in seconds. (Take the positive direction to be downward.)

(a) Find the velocity and acceleration at time t.

(b) Graph the velocity and acceleration functions.

(c) When does the mass pass through the equilibrium position for the first time?

(d) How far from its equilibrium position does the mass travel?

(e) When is the speed the greatest?

To determine

To find: The velocity and acceleration at time t.

Answer to Problem 36E

The velocity of motion at time t is $\underset{\_}{-2\sin t+3\cos t}$.

The acceleration of motion at time t is $\underset{\_}{-2\cos t-3\sin t}$.

Explanation of Solution

Given:

The equation of motion is $s\left(t\right)=2\cos t+3\sin t$, where t is in seconds and x is in centimeters.

Derivative rule:

(1) Sum Rule: $\frac{d}{dt}\left[f\left(t\right)+g\left(t\right)\right]=\frac{d}{dt}\left[f\left(t\right)\right]+\frac{d}{dt}\left[g\left(t\right)\right]$

(2) Constant Multiple Rule: $\frac{d}{dt}\left[cf\left(t\right)\right]=c\frac{d}{dt}\left[f\left(t\right)\right]$

Recall:

If $x\left(t\right)$ is a displacement of a particle and the time t is in seconds, then the velocity of the particle is $v\left(t\right)=\frac{ds}{dt}$.

If $v\left(t\right)$ is a velocity of the particle and the time t is in seconds, then the acceleration of the particle is $a\left(t\right)=\frac{dv}{dt}$.

Calculation:

Obtain the velocity at time t.

$\begin{array}{c}v\left(t\right)=\frac{d}{dt}\left(s\left(t\right)\right)\\ =\frac{d}{dt}\left(2\cos t+3\sin t\right)\end{array}$

Apply the sum rule (1),

$v\left(t\right)=\frac{d}{dt}\left[2\cos t\right]+\frac{d}{dt}\left[3\sin t\right]$

Apply the constant multiple rule (2),

$\begin{array}{c}v\left(t\right)=2\frac{d}{dt}\left[\cos t\right]+3\frac{d}{dt}\left[\sin t\right]\\ =2\left[-\sin t\right]+3\left[\cos t\right]\\ =-2\sin t+3\cos t\end{array}$

Thus, the velocity of $x\left(t\right)=2\cos t+3\sin t$ at time t is $\underset{\_}{v\left(t\right)=-2\sin t+3\cos t}$.

Obtain the acceleration at time t.

$\begin{array}{c}a\left(t\right)=\frac{d}{dt}\left(v\left(t\right)\right)\\ =\frac{d}{dt}\left(-2\sin t+3\cos t\right)\end{array}$

Apply the sum rule (1)

$a\left(t\right)=\frac{d}{dt}\left[-2\sin t\right]+\frac{d}{dt}\left[3\cos t\right]$

Apply the constant multiple rule (2)

$\begin{array}{c}a\left(t\right)=-2\frac{d}{dt}\left[\sin t\right]+3\frac{d}{dt}\left[\cos t\right]\\ =-2\left[\cos t\right]+3\left[-\sin t\right]\\ =-2\cos t-3\sin t\end{array}$

Therefore, the acceleration of $x\left(t\right)=2\cos t+3\sin t$ at time t is $\underset{\_}{a\left(t\right)=-2\cos t-3\sin t}$.

To determine

To sketch: The velocity and acceleration functions.

Explanation of Solution

From part (a), the velocity and acceleration functions are $v\left(t\right)=-2\sin t+3\cos t$ and $a\left(t\right)=-2\cos t-3\sin t$, respectively.

Use online graphing calculator and draw graph the velocity and acceleration functions as shown below in Figure 1.

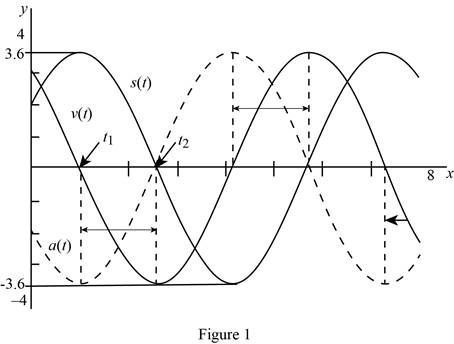
From Figure1, it is observed that the maximum position of the mass travel is approximately $3.6\text{ cm}$ and the minimum position of the mass travel is approximately $-3.6\text{ cm}$.

To determine

To find: When the mass passes through the equilibrium position for the first time.

Answer to Problem 36E

The mass passes through the equilibrium position for the first time is $t\approx 2.55\text{ s}$.

Explanation of Solution

Definition used:

The mass is in equilibrium when its acceleration is zero.

Calculation:

The equation of motion is $s\left(t\right)=2\cos t+3\sin t$.

From (a), the acceleration of $x\left(t\right)$ at time t is $a\left(t\right)=-2\cos t-3\sin t$.

Use the definition stated above and solve for $a\left(t\right)=0$.

$\begin{array}{c}-2\cos t-3\sin t=0\\ 3\sin t=-2\cos t\\ \frac{\sin t}{\cos t}=-\frac{2}{3}\\ \tan t=-\frac{2}{3}\end{array}$

Multiply the equation by ${\tan }^{-1}$,

$\begin{array}{c}ta{n}^{-1}\left(\tan t\right)=ta{n}^{-1}\left(-\frac{2}{3}\right)\\ t=ta{n}^{-1}\left(-\frac{2}{3}\right)\\ \approx -0.5880\end{array}$

Therefore, the mass of equilibrium at $t=-0.5880+n\pi$, where n is an integer.

Compute t when $n=1$.

$\begin{array}{c}t=-0.5880+\pi \\ \approx 2.5536\end{array}$

Hence, the mass passes through the equilibrium for the first time is $t\approx 2.55\text{ s}$.

To determine

To find: The distance from the equilibrium position to the final position.

Answer to Problem 36E

The mass travels about 3.6056 cm from its equilibrium position.

Explanation of Solution

From Figure1, the maximum position is $t\approx 1\text{ s}$ when $v=0$.

From part (a), $v\left(t\right)=-2\sin t+3\cos t$.

Set $v\left(t\right)=0$ and solve for t.

$\begin{array}{l}-2\sin t+3\cos t=0\\ 2\sin t=3\cos t\\ \frac{\sin t}{\cos t}=\frac{3}{2}\\ \tan t=\frac{3}{2}\end{array}$

Multiply the equation by ${\tan }^{-1}$,

$\begin{array}{c}ta{n}^{-1}\left(\tan t\right)=ta{n}^{-1}\left(\frac{3}{2}\right)\\ t=ta{n}^{-1}\left(\frac{3}{2}\right)\\ t\approx \text{0}\text{.9828}\end{array}$

Obtain $v\left(t\right)$ when $t\approx \text{0}\text{.9828}$.

$\begin{array}{c}s\left(\text{0}\text{.9828}\right)=2\cos \left(\text{0}\text{.9828}\right)+3\sin \left(\text{0}\text{.9828}\right)\\ \approx \text{3}\text{.6056}\end{array}$

Thus, the mass travels about 3.6056 cm from its equilibrium position.

To determine

To find: When is the speed greatest?

Answer to Problem 36E

The speed is maximum at $t=2.55+n\pi$.

Explanation of Solution

Note that, the velocity is zero when the mass reaches its maximum or minimum and the speed will be greatest when the mass passess through the equilibrium position.

That is, $s\left(t\right)=0$.

$\begin{array}{l}2\cos t+3\sin t=0\\ 3\sin t=-2\cos t\\ \frac{\sin t}{\cos t}=-\frac{2}{3}\\ \tan t=-\frac{2}{3}\end{array}$

Multiply the equation by ${\tan }^{-1}$,

$\begin{array}{c}ta{n}^{-1}\left(\tan t\right)=ta{n}^{-1}\left(-\frac{2}{3}\right)\\ t=ta{n}^{-1}\left(-\frac{2}{3}\right)\end{array}$

For each additional rotation of $\pi$, the speed will be greatest when $t=ta{n}^{-1}\left(-\frac{2}{3}\right)+n\pi$, n is an integer.