
Concept explainers
A semicircle with diameter PQ sits on an isosceles triangle PQR to form a region shaped like a two-dimensional ice-cream cone, as shown in the figure. If A(θ) is the area of the semicircle and B(θ) is the area of the triangle, find.
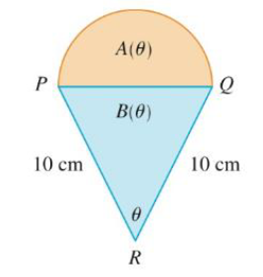
To find: The value of
Answer to Problem 48E
The value of
Explanation of Solution
Given:
The area of the semicircle is
Formula used:
The area of the semicircle is
The area of the triangle is
Calculation:
The given picture is shown in the below Figure 1.
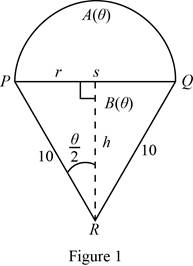
From Figure 1, the base of the triangle (PQ) is same as the diameter of semicircle (2r).
Calculate r and h.
From the triangle PSR,
And
Substitute
Thus, the area of the triangle is
From equation (1), the area if the semicircle is
Consider
Substitute
Substitute
Therefore, the value of
Chapter 3 Solutions
Single Variable Calculus: Concepts and Contexts, Enhanced Edition
Additional Math Textbook Solutions
Calculus and Its Applications (11th Edition)
Precalculus
Precalculus: A Unit Circle Approach (3rd Edition)
Precalculus: A Unit Circle Approach
Precalculus
University Calculus: Early Transcendentals, Single Variable (3rd Edition)
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





