
The motion of a spring that is subject to a frictional force or a damping force (such as a shock absorber in a car) is often modeled by the product of an exponential function and a sine or cosine function. Suppose the equation of motion of a point on such a spring is
s(t) = 2e–1.5t sin 2πt
where s is measured in centimeters and t in seconds. Find the velocity after t seconds and graph both the position and velocity functions for 0 ≤ 1 ≤ 2.
To find: The velocity after t seconds.
Answer to Problem 73E
The velocity after t seconds is
Explanation of Solution
Given:
The equation of motion of a point on such a spring is
Derivative rule:
(1) Constant Multiple Rule:
(2) Product Rule:
Recall:
If
Calculation:
Obtain the velocity at time t.
Apply the product rule (2) and the constant multiple rule (1),
Therefore, the velocity after t seconds is
To sketch: The position and velocity functions for
Graph:
Using the online graphing calculator and the draw graph below shown in Figure 1.
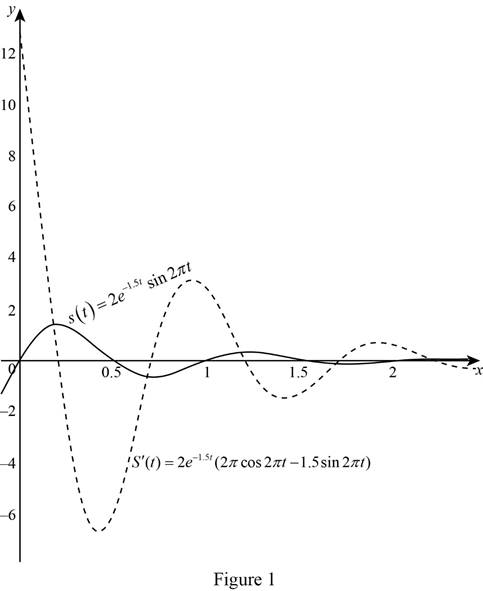
Observation:
From Figure 1, it is noticed that
(i) If
(ii) If
(iii) If
Chapter 3 Solutions
Single Variable Calculus: Concepts and Contexts, Enhanced Edition
Additional Math Textbook Solutions
Advanced Mathematical Concepts: Precalculus with Applications, Student Edition
Single Variable Calculus: Early Transcendentals (2nd Edition) - Standalone book
Calculus: Early Transcendentals (3rd Edition)
Precalculus: A Unit Circle Approach
Calculus: Single And Multivariable
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





