
Concept explainers
To show: One family of the curves are orthogonal trajectories to the other family.
Explanation of Solution
Given:
The equation of the curves
Derivative rules:
Chain rule:
Proof:
The two family of the circles
Clearly, the tangent line to the family of curves
Therefore, the two family of the circles are orthogonal trajectories of each other at
Consider two circle is intersect at non zero point
Substitute
Differentiate
Apply the chain rule and simplify the terms,
Thus, the derivative of the equation
That is, the slope of the tangent to
Differentiate
Apply the chain rule and simplify the terms,
Thus, the derivative of the equation
That is, the slope of the tangent to
Note: The two tangent lines are orthogonal if the product of their slopes is -1.
Substitute the equation (1) and (2),
Therefore, the family of the curves
Hence the required result is proved.
Graph:
The sketch of the family of the circles
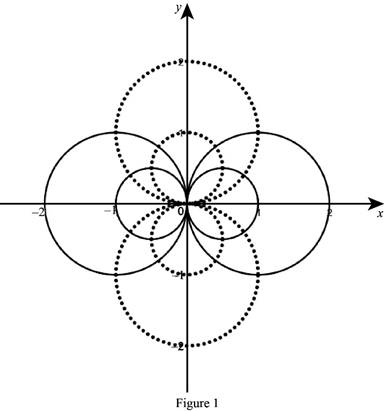
From the graph, it is observed that the two family of the circles
Chapter 3 Solutions
Single Variable Calculus: Concepts and Contexts, Enhanced Edition
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





