
Calculus (MindTap Course List)
8th Edition
ISBN: 9781285740621
Author: James Stewart
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Textbook Question
Chapter 3.7, Problem 50E
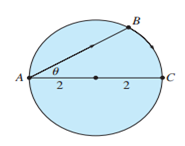
A woman at a point A on the shore of a circular lake with radius 2 mi wants to arrive at the point C diametrically opposite A on the other side of the lake in the shortest possible time (see the figure). She can walk at the rate of 4 mi/h and row a boat at 2 mi/h. How should she proceed?
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Chapter 3 Solutions
Calculus (MindTap Course List)
Ch. 3.1 - Explain the difference between an absolute minimum...Ch. 3.1 - Suppose f is a continuous function defined on a...Ch. 3.1 - For each of the numbers a, b, c, d, r, and s,...Ch. 3.1 - For each of the numbers a, b, c, d, r, and s,...Ch. 3.1 - Use the graph to state the absolute and local...Ch. 3.1 - Use the graph to state the absolute and local...Ch. 3.1 - Sketch the graph of a function f that is...Ch. 3.1 - Sketch the graph of a function f that is...Ch. 3.1 - Prob. 9ECh. 3.1 - Sketch the graph of a function f that is...
Ch. 3.1 - Prob. 11ECh. 3.1 - Prob. 12ECh. 3.1 - a Sketch the graph of a function on [1,2] that has...Ch. 3.1 - Prob. 14ECh. 3.1 - Sketch the graph of f by hand and use your sketch...Ch. 3.1 - Prob. 16ECh. 3.1 - Prob. 17ECh. 3.1 - Prob. 18ECh. 3.1 - Sketch the graph of f by hand and use your sketch...Ch. 3.1 - Prob. 20ECh. 3.1 - Prob. 21ECh. 3.1 - Prob. 22ECh. 3.1 - Sketch the graph of f by hand and use your sketch...Ch. 3.1 - Prob. 24ECh. 3.1 - Sketch the graph of f by hand and use your sketch...Ch. 3.1 - Prob. 26ECh. 3.1 - Prob. 27ECh. 3.1 - Prob. 28ECh. 3.1 - Prob. 29ECh. 3.1 - Prob. 30ECh. 3.1 - Prob. 31ECh. 3.1 - Prob. 32ECh. 3.1 - Prob. 33ECh. 3.1 - Prob. 34ECh. 3.1 - Find the critical numbers of the function....Ch. 3.1 - Prob. 36ECh. 3.1 - Find the critical numbers of the function....Ch. 3.1 - Prob. 38ECh. 3.1 - Find the critical numbers of the function....Ch. 3.1 - Prob. 40ECh. 3.1 - Find the critical numbers of the function....Ch. 3.1 - Prob. 42ECh. 3.1 - Prob. 43ECh. 3.1 - Prob. 44ECh. 3.1 - Find the absolute maximum and absolute minimum...Ch. 3.1 - Prob. 46ECh. 3.1 - Prob. 47ECh. 3.1 - Prob. 48ECh. 3.1 - Prob. 49ECh. 3.1 - Prob. 50ECh. 3.1 - Find the absolute maximum and absolute minimum...Ch. 3.1 - Prob. 52ECh. 3.1 - Find the absolute maximum and absolute minimum...Ch. 3.1 - Prob. 54ECh. 3.1 - Find the absolute maximum and absolute minimum...Ch. 3.1 - Prob. 56ECh. 3.1 - If a and b are positive numbers, find the maximum...Ch. 3.1 - Prob. 58ECh. 3.1 - Prob. 59ECh. 3.1 - Prob. 60ECh. 3.1 - Prob. 61ECh. 3.1 - Prob. 62ECh. 3.1 - Prob. 63ECh. 3.1 - An object with weight W is dragged along a...Ch. 3.1 - The water level, measured in feet above mean sea...Ch. 3.1 - On May 7, 1992, the space shuttle Endeavour was...Ch. 3.1 - Prob. 67ECh. 3.1 - Prob. 68ECh. 3.1 - Prove that the function f(x)=x101+x51+x+1 has...Ch. 3.1 - If f has a local minimum value at c, show that the...Ch. 3.1 - Prove Fermats Theorem for the case in which f has...Ch. 3.1 - Prob. 72ECh. 3.2 - The graph of a function f is shown. Verify that f...Ch. 3.2 - Draw the graph of a function defined on 0, 8 such...Ch. 3.2 - The graph of a function g is shown. a Verify that...Ch. 3.2 - Prob. 4ECh. 3.2 - Prob. 5ECh. 3.2 - Prob. 6ECh. 3.2 - 5-8 Verify that the function satisfies the three...Ch. 3.2 - Prob. 8ECh. 3.2 - Let f(x)=1x2/3. Show that f(1)=f(1) but there is...Ch. 3.2 - Let f(x)=tanx. Show that f(0)=f() but there is no...Ch. 3.2 - 11-14 Verify that the function satisfies the...Ch. 3.2 - Prob. 12ECh. 3.2 - 11-14 Verify that the function satisfies the...Ch. 3.2 - Prob. 14ECh. 3.2 - Prob. 15ECh. 3.2 - 15-16 Find the number c that satisfies the...Ch. 3.2 - Let f(x)=(x3)2. Show that there is no value of c...Ch. 3.2 - Let f(x)=2|2x1|. Show that there is no value of c...Ch. 3.2 - 19-20 Show that the equation has exactly one real...Ch. 3.2 - Prob. 20ECh. 3.2 - Show that the equation x315x+c=0 has at most one...Ch. 3.2 - Show that the equation x4+4x+c=0 has at most two...Ch. 3.2 - a Show that a polynomial of degree 3 has at most...Ch. 3.2 - Prob. 24ECh. 3.2 - If f(1)=10 and f(x)2 for 1x4, how small can f(4)...Ch. 3.2 - Prob. 26ECh. 3.2 - Prob. 27ECh. 3.2 - Suppose that f and g are continuous on a, b and...Ch. 3.2 - Prob. 29ECh. 3.2 - Suppose f is an odd function and is differentiable...Ch. 3.2 - Prob. 31ECh. 3.2 - Prob. 32ECh. 3.2 - Prob. 33ECh. 3.2 - At 2:00 pm a cars speedometer reads 30 mi/h. At...Ch. 3.2 - Two runners start a race at the same time and...Ch. 3.2 - A number a is called a fixed point of a function f...Ch. 3.3 - 1-2 Use the given graph of f to find the...Ch. 3.3 - 1-2 Use the given graph of f to find the...Ch. 3.3 - Suppose you are given a formula for a function f....Ch. 3.3 - a State the First Derivative Test. b State the...Ch. 3.3 - 5-6 The graph of the derivative f of a function f...Ch. 3.3 - 5-6 The graph of the derivative f of a function f...Ch. 3.3 - In each part state the x-coordinates of the...Ch. 3.3 - The graph of the first derivative f of a function...Ch. 3.3 - Prob. 9ECh. 3.3 - Prob. 10ECh. 3.3 - Prob. 11ECh. 3.3 - Prob. 12ECh. 3.3 - 9-14 a Find the intervals on which f is increasing...Ch. 3.3 - Prob. 14ECh. 3.3 - 15-17 Find the local maximum and minimum values of...Ch. 3.3 - Prob. 16ECh. 3.3 - 15-17 Find the local maximum and minimum values of...Ch. 3.3 - Prob. 18ECh. 3.3 - Prob. 19ECh. 3.3 - Prob. 20ECh. 3.3 - Prob. 21ECh. 3.3 - Prob. 22ECh. 3.3 - Prob. 23ECh. 3.3 - Prob. 24ECh. 3.3 - Prob. 25ECh. 3.3 - 20-27 Sketch the graph of a function that...Ch. 3.3 - Prob. 27ECh. 3.3 - Prob. 28ECh. 3.3 - Suppose f is a continuous function where f(x)0 for...Ch. 3.3 - The graph of a function y=f(x) is shown. At which...Ch. 3.3 - 31-32 The graph of the derivative f of a...Ch. 3.3 - 31-32 The graph of the derivative f of a...Ch. 3.3 - Prob. 33ECh. 3.3 - Prob. 34ECh. 3.3 - Prob. 35ECh. 3.3 - 33-44 a Find the intervals of increase or...Ch. 3.3 - 33-44 a Find the intervals of increase or...Ch. 3.3 - Prob. 38ECh. 3.3 - 33-44 a Find the intervals of increase or...Ch. 3.3 - Prob. 40ECh. 3.3 - Prob. 41ECh. 3.3 - Prob. 42ECh. 3.3 - 33-44 a Find the intervals of increase or...Ch. 3.3 - 33-44 a Find the intervals of increase or...Ch. 3.3 - Prob. 45ECh. 3.3 - Prob. 46ECh. 3.3 - Prob. 47ECh. 3.3 - 47-48 a Use a graph of f to estimate the maximum...Ch. 3.3 - Prob. 49ECh. 3.3 - Prob. 50ECh. 3.3 - Prob. 51ECh. 3.3 - Prob. 52ECh. 3.3 - A graph of a population of yeast cells in a new...Ch. 3.3 - In an episode of The Simpsons television show,...Ch. 3.3 - Prob. 55ECh. 3.3 - Prob. 56ECh. 3.3 - Prob. 57ECh. 3.3 - Prob. 58ECh. 3.3 - Prob. 59ECh. 3.3 - Prob. 60ECh. 3.3 - a If the function f(x)=x3+ax2+bx has the local...Ch. 3.3 - Prob. 62ECh. 3.3 - Prob. 63ECh. 3.3 - Prob. 64ECh. 3.3 - Prob. 65ECh. 3.3 - Prob. 66ECh. 3.3 - Prob. 67ECh. 3.3 - Prob. 68ECh. 3.3 - Show that a cubic function a third-degree...Ch. 3.3 - For what values of c does the polynomial...Ch. 3.3 - Prove that if (c,f(c)) is a point of inflection of...Ch. 3.3 - Show that if f(x)=x4, then f(0)=0, but 0, 0 is not...Ch. 3.3 - Show that the function g(x)=x|x| has an inflection...Ch. 3.3 - Prob. 74ECh. 3.3 - Prob. 75ECh. 3.3 - Prob. 76ECh. 3.3 - The three cases in the First Derivative Test cover...Ch. 3.4 - Explain in your own words the meaning of each of...Ch. 3.4 - a Can the graph of y=f(x) intersect a vertical...Ch. 3.4 - For the function f whose graph is given, state the...Ch. 3.4 - For the function g whose graph is given, state the...Ch. 3.4 - Prob. 5ECh. 3.4 - Prob. 6ECh. 3.4 - Prob. 7ECh. 3.4 - 7-8 Evaluate the limit and justify each step by...Ch. 3.4 - Prob. 9ECh. 3.4 - Prob. 10ECh. 3.4 - Prob. 11ECh. 3.4 - Prob. 12ECh. 3.4 - 9-32 Find the limit or show that it does not...Ch. 3.4 - 9-32 Find the limit or show that it does not...Ch. 3.4 - 9-32 Find the limit or show that it does not...Ch. 3.4 - 9-32 Find the limit or show that it does not...Ch. 3.4 - 9-32 Find the limit or show that it does not...Ch. 3.4 - 9-32 Find the limit or show that it does not...Ch. 3.4 - 9-32 Find the limit or show that it does not...Ch. 3.4 - 9-32 Find the limit or show that it does not...Ch. 3.4 - 9-32 Find the limit or show that it does not...Ch. 3.4 - 9-32 Find the limit or show that it does not...Ch. 3.4 - 9-32 Find the limit or show that it does not...Ch. 3.4 - 9-32 Find the limit or show that it does not...Ch. 3.4 - 9-32 Find the limit or show that it does not...Ch. 3.4 - 9-32 Find the limit or show that it does not...Ch. 3.4 - 9-32 Find the limit or show that it does not...Ch. 3.4 - 9-32 Find the limit or show that it does not...Ch. 3.4 - 9-32 Find the limit or show that it does not...Ch. 3.4 - 9-32 Find the limit or show that it does not...Ch. 3.4 - 9-32 Find the limit or show that it does not...Ch. 3.4 - 9-32 Find the limit or show that it does not...Ch. 3.4 - a Estimate the value of limx(x2+x+1+x) by graphing...Ch. 3.4 - a Use a graph of f(x)=3x2+8x+63x2+3x+1 to estimate...Ch. 3.4 - 35-40 Find the horizontal and vertical asymptotes...Ch. 3.4 - 35-40 Find the horizontal and vertical asymptotes...Ch. 3.4 - 35-40 Find the horizontal and vertical asymptotes...Ch. 3.4 - 35-40 Find the horizontal and vertical asymptotes...Ch. 3.4 - 35-40 Find the horizontal and vertical asymptotes...Ch. 3.4 - Prob. 40ECh. 3.4 - Prob. 41ECh. 3.4 - Prob. 42ECh. 3.4 - Let P and Q be polynomials. Find limxP(x)Q(x) if...Ch. 3.4 - Prob. 44ECh. 3.4 - Find a formula for a function / that satisfies the...Ch. 3.4 - Prob. 46ECh. 3.4 - A function f is a ratio of quadratic functions and...Ch. 3.4 - Prob. 48ECh. 3.4 - 48-51 Find the horizontal asymptotes of the curve...Ch. 3.4 - 48-51 Find the horizontal asymptotes of the curve...Ch. 3.4 - Prob. 51ECh. 3.4 - Prob. 52ECh. 3.4 - Prob. 53ECh. 3.4 - Prob. 54ECh. 3.4 - Prob. 55ECh. 3.4 - Prob. 56ECh. 3.4 - 57-60 Sketch the graph of a function that...Ch. 3.4 - Prob. 58ECh. 3.4 - Prob. 59ECh. 3.4 - Prob. 60ECh. 3.4 - a Use the Squeeze Theorem to evaluate limxsinxx. b...Ch. 3.4 - By the end behavior of a function we mean the...Ch. 3.4 - Prob. 63ECh. 3.4 - a A tank contains 5000 L of pure water. Brine that...Ch. 3.4 - Prob. 65ECh. 3.4 - Prob. 66ECh. 3.4 - For the limit limx13xx2+1=3 illustrate Definition...Ch. 3.4 - Prob. 68ECh. 3.4 - Prob. 69ECh. 3.4 - Prob. 70ECh. 3.4 - Prob. 71ECh. 3.4 - Prob. 72ECh. 3.4 - Prob. 73ECh. 3.4 - Prob. 74ECh. 3.5 - 1-40 Use the guidelines of this section to sketch...Ch. 3.5 - Prob. 2ECh. 3.5 - 1-40 Use the guidelines of this section to sketch...Ch. 3.5 - Prob. 4ECh. 3.5 - 1-40 Use the guidelines of this section to sketch...Ch. 3.5 - Prob. 6ECh. 3.5 - 1-40 Use the guidelines of this section to sketch...Ch. 3.5 - Prob. 8ECh. 3.5 - Prob. 9ECh. 3.5 - Prob. 10ECh. 3.5 - 1-40 Use the guidelines of this section to sketch...Ch. 3.5 - Prob. 12ECh. 3.5 - 1-40 Use the guidelines of this section to sketch...Ch. 3.5 - Prob. 14ECh. 3.5 - 1-40 Use the guidelines of this section to sketch...Ch. 3.5 - Prob. 16ECh. 3.5 - 1-40 Use the guidelines of this section to sketch...Ch. 3.5 - Prob. 18ECh. 3.5 - 1-40 Use the guidelines of this section to sketch...Ch. 3.5 - Prob. 20ECh. 3.5 - Prob. 21ECh. 3.5 - Prob. 22ECh. 3.5 - Prob. 23ECh. 3.5 - Prob. 24ECh. 3.5 - Prob. 25ECh. 3.5 - Prob. 26ECh. 3.5 - Prob. 27ECh. 3.5 - Prob. 28ECh. 3.5 - 1-40 Use the guidelines of this section to sketch...Ch. 3.5 - Prob. 30ECh. 3.5 - Prob. 31ECh. 3.5 - Prob. 32ECh. 3.5 - Prob. 33ECh. 3.5 - Prob. 34ECh. 3.5 - Prob. 35ECh. 3.5 - Prob. 36ECh. 3.5 - 1-40 Use the guidelines of this section to sketch...Ch. 3.5 - Prob. 38ECh. 3.5 - Prob. 39ECh. 3.5 - Prob. 40ECh. 3.5 - Prob. 41ECh. 3.5 - Prob. 42ECh. 3.5 - The figure shows a beam of length L embedded in...Ch. 3.5 - Coulombs Law states that the force of attraction...Ch. 3.5 - 4548 Find an equation of the slant asymptote. Do...Ch. 3.5 - Prob. 46ECh. 3.5 - Prob. 47ECh. 3.5 - Prob. 48ECh. 3.5 - Prob. 49ECh. 3.5 - Prob. 50ECh. 3.5 - Prob. 51ECh. 3.5 - Prob. 52ECh. 3.5 - 4954 Use the guidelines of this section to sketch...Ch. 3.5 - Prob. 54ECh. 3.5 - Prob. 55ECh. 3.5 - Prob. 56ECh. 3.5 - Prob. 57ECh. 3.5 - Prob. 58ECh. 3.5 - Prob. 59ECh. 3.5 - Use the asymptotic behavior of f(x)=cosx+1/x2 to...Ch. 3.6 - 18 Produce graphs of f that reveal all the...Ch. 3.6 - Prob. 2ECh. 3.6 - Prob. 3ECh. 3.6 - Prob. 4ECh. 3.6 - Prob. 5ECh. 3.6 - Prob. 6ECh. 3.6 - Prob. 7ECh. 3.6 - Prob. 8ECh. 3.6 - Prob. 9ECh. 3.6 - Prob. 10ECh. 3.6 - Prob. 11ECh. 3.6 - Prob. 12ECh. 3.6 - Prob. 13ECh. 3.6 - Prob. 14ECh. 3.6 - Prob. 15ECh. 3.6 - Prob. 16ECh. 3.6 - Prob. 17ECh. 3.6 - Prob. 18ECh. 3.6 - Prob. 19ECh. 3.6 - Prob. 20ECh. 3.6 - Prob. 21ECh. 3.6 - Prob. 22ECh. 3.6 - Prob. 23ECh. 3.6 - Prob. 24ECh. 3.6 - Prob. 25ECh. 3.6 - Prob. 26ECh. 3.6 - Prob. 27ECh. 3.6 - Prob. 28ECh. 3.7 - Consider the following problem: Find two numbers...Ch. 3.7 - Find two numbers whose difference is 100 and whose...Ch. 3.7 - Find two positive numbers whose product is 100 and...Ch. 3.7 - The sum of two positive numbers is 16. What is the...Ch. 3.7 - What is the maximum vertical distance between the...Ch. 3.7 - Prob. 6ECh. 3.7 - Find the dimensions of a rectangle with perimeter...Ch. 3.7 - Find the dimensions of a rectangle with area 1000...Ch. 3.7 - A model used for the yield y of an agricultural...Ch. 3.7 - The rate in mg carbon/m3/h at which photosynthesis...Ch. 3.7 - Consider the following problem: A farmer with 750...Ch. 3.7 - Consider the following problem: A box with an open...Ch. 3.7 - A farmer wants to fence in an area of 1.5 million...Ch. 3.7 - Prob. 14ECh. 3.7 - If 1200 cm2 of material is available to make a box...Ch. 3.7 - Prob. 16ECh. 3.7 - Do Exercise 16 assuming the container has a fid...Ch. 3.7 - Prob. 18ECh. 3.7 - If the farmer in Exercise 18 wants to enclose 8000...Ch. 3.7 - a Show that of all the rectangles with a given...Ch. 3.7 - Find the point on the line y=2x+3 that is closest...Ch. 3.7 - Prob. 22ECh. 3.7 - Find the points on the ellipse 4x2+y2=4 that are...Ch. 3.7 - Find, correct to two decimal places, the...Ch. 3.7 - Find the dimensions of the rectangle of largest...Ch. 3.7 - Find the area of the largest rectangle that can be...Ch. 3.7 - Find the dimensions of the rectangle of largest...Ch. 3.7 - Find the area of the largest trapezoid that can be...Ch. 3.7 - Find the dimensions of the isosceles triangle of...Ch. 3.7 - If the two equal sides of an isosceles triangle...Ch. 3.7 - Prob. 31ECh. 3.7 - A right circular cylinder is inscribed in a cone...Ch. 3.7 - A right circular cylinder is inscribed in a sphere...Ch. 3.7 - A Norman window has the shape of a rectangle...Ch. 3.7 - Prob. 35ECh. 3.7 - A poster is to have an area of 180 in 2 with...Ch. 3.7 - A piece of wire 10 m long is cut into two pieces....Ch. 3.7 - Solve Exercise 37 if one piece is bent into a...Ch. 3.7 - If you are offered one slice from a round pizza in...Ch. 3.7 - Prob. 40ECh. 3.7 - Prob. 41ECh. 3.7 - A cone-shaped paper drinking cup is to be made to...Ch. 3.7 - A cone with height h is inscribed in a larger cone...Ch. 3.7 - Prob. 44ECh. 3.7 - Prob. 45ECh. 3.7 - For a fish swimming at a speed v relative to the...Ch. 3.7 - In a beehive, each cell is a regular hexagonal...Ch. 3.7 - A boat leaves a dock at 2:00 PM and travels due...Ch. 3.7 - Solve the problem in Example 4 if the river is 5...Ch. 3.7 - A woman at a point A on the shore of a circular...Ch. 3.7 - An oil refinery is located on the north bank of a...Ch. 3.7 - Suppose the refinery in Exercise 51 is located 1...Ch. 3.7 - Prob. 53ECh. 3.7 - Prob. 54ECh. 3.7 - Let a and b be positive numbers. Find the length...Ch. 3.7 - Prob. 56ECh. 3.7 - Prob. 57ECh. 3.7 - What is the smallest possible area of the triangle...Ch. 3.7 - Prob. 59ECh. 3.7 - Prob. 60ECh. 3.7 - Prob. 61ECh. 3.7 - During the summer months Terry makes and sells...Ch. 3.7 - A retailer has been selling 1200 tablet computers...Ch. 3.7 - A company operates 16 oil wells in a designated...Ch. 3.7 - Show that of all the isosceles triangles with a...Ch. 3.7 - Prob. 66ECh. 3.7 - Consider the tangent line to the ellipse...Ch. 3.7 - The frame for a kite is to be made from six pieces...Ch. 3.7 - A point P needs to be located somewhere on the...Ch. 3.7 - The graph shows the fuel consumption c of a car...Ch. 3.7 - Let v1 be the velocity of light in air and v2 the...Ch. 3.7 - Two vertical poles PQ and ST are secured by a rope...Ch. 3.7 - The upper right-hand corner of a piece of paper,...Ch. 3.7 - A steel pipe is being carried down a hallway 9 ft...Ch. 3.7 - An observer stands at a point P, one unit away...Ch. 3.7 - A rain gutter is to be constructed from a metal...Ch. 3.7 - Prob. 77ECh. 3.7 - The blood vascular system consists of blood...Ch. 3.7 - Ornithologists have determined that some species...Ch. 3.7 - Two light sources of identical strength are placed...Ch. 3.8 - The figure shows the graph of a function f....Ch. 3.8 - Prob. 2ECh. 3.8 - Suppose the tangent line to the curve y=f(x) at...Ch. 3.8 - For each initial approximation, determine...Ch. 3.8 - For which of the initial approximations x1=a,b,c,...Ch. 3.8 - Prob. 6ECh. 3.8 - Prob. 7ECh. 3.8 - Prob. 8ECh. 3.8 - Prob. 9ECh. 3.8 - Prob. 10ECh. 3.8 - Prob. 11ECh. 3.8 - Prob. 12ECh. 3.8 - Prob. 13ECh. 3.8 - Prob. 14ECh. 3.8 - Prob. 15ECh. 3.8 - Prob. 16ECh. 3.8 - Prob. 17ECh. 3.8 - Prob. 18ECh. 3.8 - Prob. 19ECh. 3.8 - Prob. 20ECh. 3.8 - Prob. 21ECh. 3.8 - Prob. 22ECh. 3.8 - Prob. 23ECh. 3.8 - Prob. 24ECh. 3.8 - Prob. 25ECh. 3.8 - Prob. 26ECh. 3.8 - Prob. 27ECh. 3.8 - Prob. 28ECh. 3.8 - Explain why Newtons method doesnt work for finding...Ch. 3.8 - a Use Newtons method with x1=1 to find the root of...Ch. 3.8 - Prob. 31ECh. 3.8 - Prob. 32ECh. 3.8 - a Use Newtons method to find the critical numbers...Ch. 3.8 - Prob. 34ECh. 3.8 - Use Newtons method to find the coordinates of the...Ch. 3.8 - Prob. 36ECh. 3.8 - Use Newtons method to find the coordinates,...Ch. 3.8 - In the figure, the length of the chord AB is 4 cm...Ch. 3.8 - Prob. 39ECh. 3.8 - Prob. 40ECh. 3.9 - Find the most general antiderivative of the...Ch. 3.9 - Prob. 2ECh. 3.9 - Find the most general antiderivative of the...Ch. 3.9 - Prob. 4ECh. 3.9 - Find the most general antiderivative of the...Ch. 3.9 - Prob. 6ECh. 3.9 - Prob. 7ECh. 3.9 - Prob. 8ECh. 3.9 - Prob. 9ECh. 3.9 - Prob. 10ECh. 3.9 - Prob. 11ECh. 3.9 - Prob. 12ECh. 3.9 - Find the most general antiderivative of the...Ch. 3.9 - Prob. 14ECh. 3.9 - Find the most general antiderivative of the...Ch. 3.9 - Prob. 16ECh. 3.9 - Prob. 17ECh. 3.9 - Prob. 18ECh. 3.9 - Prob. 19ECh. 3.9 - Prob. 20ECh. 3.9 - Prob. 21ECh. 3.9 - Prob. 22ECh. 3.9 - Prob. 23ECh. 3.9 - Prob. 24ECh. 3.9 - Prob. 25ECh. 3.9 - Prob. 26ECh. 3.9 - Prob. 27ECh. 3.9 - Prob. 28ECh. 3.9 - 23-42 Find f. f(x)=1+3x,f(4)=25Ch. 3.9 - Prob. 30ECh. 3.9 - 23-42 Find f. f(x)=x(6+5x),f(1)=10Ch. 3.9 - Prob. 32ECh. 3.9 - Prob. 33ECh. 3.9 - Prob. 34ECh. 3.9 - Prob. 35ECh. 3.9 - Prob. 36ECh. 3.9 - Prob. 37ECh. 3.9 - Prob. 38ECh. 3.9 - 23-42 Find f. f(x)=4+6x+24x2,f(0)=3,f(1)=10Ch. 3.9 - Prob. 40ECh. 3.9 - Prob. 41ECh. 3.9 - Prob. 42ECh. 3.9 - Prob. 43ECh. 3.9 - Prob. 44ECh. 3.9 - 45-46 The graph of a function f is shown. Which...Ch. 3.9 - 45-46 The graph of a function f is shown. Which...Ch. 3.9 - The graph of a function is shown in the figure....Ch. 3.9 - The graph of the velocity function of a particle...Ch. 3.9 - Prob. 49ECh. 3.9 - Prob. 50ECh. 3.9 - Prob. 51ECh. 3.9 - Prob. 52ECh. 3.9 - Prob. 53ECh. 3.9 - Prob. 54ECh. 3.9 - Prob. 55ECh. 3.9 - Prob. 56ECh. 3.9 - Prob. 57ECh. 3.9 - Prob. 58ECh. 3.9 - A stone is dropped from the upper observation deck...Ch. 3.9 - Show that for motion in a straight line with...Ch. 3.9 - An object is projected upward with initial...Ch. 3.9 - Prob. 62ECh. 3.9 - Prob. 63ECh. 3.9 - If a diver of mass m stands at the end of a diving...Ch. 3.9 - Prob. 65ECh. 3.9 - Prob. 66ECh. 3.9 - Since raindrops grow as they fall, their surface...Ch. 3.9 - Prob. 68ECh. 3.9 - Prob. 69ECh. 3.9 - Prob. 70ECh. 3.9 - Prob. 71ECh. 3.9 - A model rocket is fired vertically upward from...Ch. 3.9 - Prob. 73ECh. 3.R - Prob. 1CCCh. 3.R - Prob. 2CCCh. 3.R - a State Fermats Theorem. b Define a critical...Ch. 3.R - Prob. 4CCCh. 3.R - Prob. 5CCCh. 3.R - Prob. 6CCCh. 3.R - Prob. 7CCCh. 3.R - Prob. 8CCCh. 3.R - If you have a graphing calculator or computer, why...Ch. 3.R - Prob. 10CCCh. 3.R - Prob. 11CCCh. 3.R - Prob. 1TFQCh. 3.R - Prob. 2TFQCh. 3.R - Prob. 3TFQCh. 3.R - Prob. 4TFQCh. 3.R - Determine whether the statement is true or false....Ch. 3.R - Prob. 6TFQCh. 3.R - Prob. 7TFQCh. 3.R - Prob. 8TFQCh. 3.R - Prob. 9TFQCh. 3.R - Prob. 10TFQCh. 3.R - Prob. 11TFQCh. 3.R - Prob. 12TFQCh. 3.R - Prob. 13TFQCh. 3.R - Prob. 14TFQCh. 3.R - Prob. 15TFQCh. 3.R - Prob. 16TFQCh. 3.R - Prob. 17TFQCh. 3.R - Prob. 18TFQCh. 3.R - Prob. 19TFQCh. 3.R - Prob. 1ECh. 3.R - Prob. 2ECh. 3.R - 1-6 Find the local and absolute extreme values of...Ch. 3.R - Prob. 4ECh. 3.R - 1-6 Find the local and absolute extreme values of...Ch. 3.R - Prob. 6ECh. 3.R - Prob. 7ECh. 3.R - 7-12 Find the limit. limtt3t+2(2t1)(t2+t+1)Ch. 3.R - Prob. 9ECh. 3.R - Prob. 10ECh. 3.R - 7-12 Find the limit. limx(4x2+3x2x)Ch. 3.R - Prob. 12ECh. 3.R - 13-15 Sketch the graph of a function that...Ch. 3.R - Prob. 14ECh. 3.R - Prob. 15ECh. 3.R - The figure shows the graph of the derivative f of...Ch. 3.R - 17-28 Use the guidelines of Section 3.5 to sketch...Ch. 3.R - Prob. 18ECh. 3.R - 17-28 Use the guidelines of Section 3.5 to sketch...Ch. 3.R - 17-28 Use the guidelines of Section 3.5 to sketch...Ch. 3.R - 17-28 Use the guidelines of Section 3.5 to sketch...Ch. 3.R - Prob. 22ECh. 3.R - Prob. 23ECh. 3.R - Prob. 24ECh. 3.R - Prob. 25ECh. 3.R - Prob. 26ECh. 3.R - Prob. 27ECh. 3.R - Prob. 28ECh. 3.R - Prob. 29ECh. 3.R - Prob. 30ECh. 3.R - Prob. 31ECh. 3.R - Prob. 32ECh. 3.R - Show that the equation 3x+2cosx+5=0 has exactly...Ch. 3.R - Prob. 34ECh. 3.R - By applying the Mean Value Theorem to the function...Ch. 3.R - For what values of the constants a and b is 1, 3 a...Ch. 3.R - Prob. 37ECh. 3.R - Find two positive integers such that the sum of...Ch. 3.R - Show that the shortest distance from the point...Ch. 3.R - Prob. 40ECh. 3.R - Find the smallest possible area of an isosceles...Ch. 3.R - Prob. 42ECh. 3.R - Prob. 43ECh. 3.R - Prob. 44ECh. 3.R - Prob. 45ECh. 3.R - Prob. 46ECh. 3.R - A hockey team plays in an arena with a seating...Ch. 3.R - Prob. 48ECh. 3.R - Prob. 49ECh. 3.R - Prob. 50ECh. 3.R - Prob. 51ECh. 3.R - Prob. 52ECh. 3.R - Prob. 53ECh. 3.R - Prob. 54ECh. 3.R - 55-58 Find f. f(t)=2t3sint,f(0)=5Ch. 3.R - Prob. 56ECh. 3.R - Prob. 57ECh. 3.R - Prob. 58ECh. 3.R - Prob. 59ECh. 3.R - Prob. 60ECh. 3.R - Prob. 61ECh. 3.R - Prob. 62ECh. 3.R - Prob. 63ECh. 3.R - In an automobile race along a straight road, car A...Ch. 3.R - A rectangular beam will be cut from a cylindrical...Ch. 3.R - If a projectile is fired with an initial velocity...Ch. 3.R - Prob. 67ECh. 3.R - Prob. 68ECh. 3.P - Show that |sinxcosx|2 for all xCh. 3.P - Prob. 2PCh. 3.P - Show that the inflection points of the curve...Ch. 3.P - Find the point on the parabola y=1x2 at which the...Ch. 3.P - Prob. 5PCh. 3.P - Water is flowing at a constant rate into a...Ch. 3.P - Prob. 7PCh. 3.P - Prob. 8PCh. 3.P - Prob. 9PCh. 3.P - An isosceles triangle is circumscribed about the...Ch. 3.P - The line y=mx+b intersects the parabola y=x2 in...Ch. 3.P - Prob. 12PCh. 3.P - Prob. 13PCh. 3.P - Prob. 14PCh. 3.P - Prob. 15PCh. 3.P - a Let ABC be a triangle with right angle A and...Ch. 3.P - Prob. 17PCh. 3.P - ABCD is a square piece of paper with sides of...Ch. 3.P - Prob. 19PCh. 3.P - For what values of c is there is a straight line...Ch. 3.P - One of the problems posed by the Marquis de...Ch. 3.P - Prob. 22PCh. 3.P - Assume that a snowball melts so that its volume...Ch. 3.P - A hemispherical bubble is placed on a spherical...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Recommended textbooks for you
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning

Calculus: Early Transcendentals
Calculus
ISBN:9781285741550
Author:James Stewart
Publisher:Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:9780134438986
Author:Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:9780134763644
Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:9781319050740
Author:Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:W. H. Freeman


Calculus: Early Transcendental Functions
Calculus
ISBN:9781337552516
Author:Ron Larson, Bruce H. Edwards
Publisher:Cengage Learning
UG/ linear equation in linear algebra; Author: The Gate Academy;https://www.youtube.com/watch?v=aN5ezoOXX5A;License: Standard YouTube License, CC-BY
System of Linear Equations-I; Author: IIT Roorkee July 2018;https://www.youtube.com/watch?v=HOXWRNuH3BE;License: Standard YouTube License, CC-BY