Chapter 3.8, Problem 3E

A particle moves according to a law of motion s = f(t), t ≥ 0, where t is measured in seconds and s in feet.

(a) Find the velocity at time t.

(b) What is the velocity after 1 second?

(c) When is the particle at rest?

(d) When is the particle moving in the positive direction?

(e) Find the total distance traveled during the first 6 seconds.

(f) Draw a diagram like Figure 2 to illustrate the motion of the particle.

(g) Find the acceleration at time t and after 1 second.

(h) Graph the position, velocity, and acceleration functions for 0 ≤ t ≤ 6.

(i) When is the particle speeding up? When is it slowing down?

FIGURE 2

f(t) = sin(πt/2)

To determine

To find: The velocity at time t.

Answer to Problem 3E

The velocity at time is $\underset{\_}{f\text{'}\left(t\right)=\frac{\pi }{2}\cos \left(\frac{\pi t}{2}\right)\text{ft/sec}}$.

Explanation of Solution

Given:

The given equation is as below.

$s=f\left(t\right)=\sin \left(\frac{\pi t}{2}\right)$ (1)

Calculation:

Calculate the velocity at time $t$.

Differentiate the equation (1) with respect to time.

$v\left(t\right)=f\text{'}\left(t\right)=\cos \left(\frac{\pi t}{2}\right).\frac{\pi }{2}$

$v\left(t\right)=f\text{'}\left(t\right)=\frac{\pi }{2}\cos \left(\frac{\pi t}{2}\right)\raisebox{1ex}{$\text{ft}$}\!\left/ \!\raisebox{-1ex}{$\text{sec}$}\right.$ (2)

Therefore, the velocity at time $t$ is $\underset{\_}{f\text{'}\left(t\right)=\frac{\pi }{2}\cos \left(\frac{\pi t}{2}\right)\text{ft/sec}}$.

To determine

To find: The velocity after 1 second.

Answer to Problem 3E

The velocity after 1 second is $\underset{\_}{v\left(1\right)=0\text{ft/sec}}$.

Explanation of Solution

Calculate the velocity after 1 second.

Substitute 1 for $t$ in the equation (2).

$\begin{array}{c}v\left(t\right)=f\text{'}\left(t\right)=\frac{\pi }{2}\cos \left(\frac{\pi t}{2}\right)\\ v\left(1\right)=f\text{'}\left(1\right)=\frac{\pi }{2}\cos \left(\frac{\pi \left(1\right)}{2}\right)\\ v\left(1\right)=0\text{ft/sec}\end{array}$

Therefore, the velocity after 1 second is $\underset{\_}{v\left(1\right)=0\text{ft/sec}}$.

To determine

To find: The time when particle at rest.

Answer to Problem 3E

The particle never is at rest when $\underset{\_}{t=1+2n}$.

Explanation of Solution

Calculate the time when particle will be at rest.

The velocity will be zero, when the particle is at rest.

Substitute 0 for $v\left(t\right)$ in the equation (2).

$\begin{array}{c}v\left(t\right)=\frac{\pi }{2}\cos \left(\frac{\pi t}{2}\right)\\ 0=\frac{\pi }{2}\cos \left(\frac{\pi t}{2}\right)\\ \cos \left(\frac{\pi t}{2}\right)=0\\ \left(\frac{\pi t}{2}\right)=\frac{\pi }{2}+n\pi \\ t=\left(\frac{\pi }{2}+n\pi \right)\frac{2}{\pi }\\ t=1+2n\end{array}$

Here, $n$ is the non-negative integer where $t\ge 0$.

To determine

To find: The particle moving in the positive direction.

Answer to Problem 3E

The velocity of particle always moves in positive direction when $\underset{\_}{0<t<1},\underset{\_}{3<t<5},\underset{\_}{7<t<9}$.

Explanation of Solution

Calculate the time at which the particle will be moving in the positive direction.

The particle will move in positive direction when $v\left(t\right)>0$, and the equation from part (c), the velocity changes its sign at every positive odd integer. Therefore, the intervals are $0<t<1,3<t<5,7<t<9$ and so on.

To determine

To find: The total distance traveled during the first 6 seconds.

Answer to Problem 3E

The total distance travelled during first 6 second is $\underset{\_}{f\left(6\right)=6\text{ft}}$.

Explanation of Solution

Calculate the total distance traveled during first 6 seconds.

Here, the velocity changes from 1, 3 and 5 which appears in the interval of [0,6].

Substitute 1 and 0 for $t$ in the equation (1).

$\begin{array}{l}\left|f\left(1\right)-f\left(0\right)\right|=\left|\sin \frac{\pi \left(1\right)}{2}-\sin \frac{\pi \left(0\right)}{2}\right|=\left|1-0\right|=1\\ \left|f\left(3\right)-f\left(1\right)\right|=\left|\sin \frac{\pi \left(3\right)}{2}-\sin \frac{\pi \left(1\right)}{2}\right|=\left|-1-1\right|=2\\ \left|f\left(5\right)-f\left(3\right)\right|=\left|\sin \frac{\pi \left(5\right)}{2}-\sin \frac{\pi \left(3\right)}{2}\right|=\left|1-\left(-1\right)\right|=2\\ \left|f\left(6\right)-f\left(5\right)\right|=\left|\sin \frac{\pi \left(6\right)}{2}-\sin \frac{\pi \left(5\right)}{2}\right|=\left|0-1\right|=1\end{array}$

The total distance travelled is as below.

$\begin{array}{c}f\left(t\right)=1+2+2+1\\ =6\text{ft}\end{array}$

Therefore, the total distance travelled during first 6 seconds is $\underset{\_}{f\left(6\right)=6\text{ft}}$.

To determine

To find: The diagram to illustrate the motion of the particle.

Answer to Problem 3E

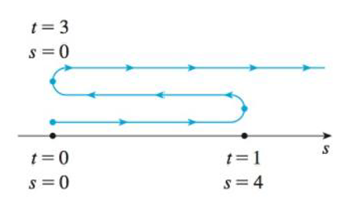
The diagram to illustrate the motion of particle is shown in the figure (1).

Explanation of Solution

Calculate the distance s using the expression.

$s=\sin \frac{\pi t}{2}$

Substitute 0 for $t$ in the above equation.

$\begin{array}{l}s=\sin \frac{\pi t}{2}\\ s=\sin \frac{\pi \left(0\right)}{2}\\ s=0\end{array}$

Calculate the value of t and s as shown in the table (1).

t	s
0	0
1	1
3	-1
5	1
6	0

Show the diagram to illustrate the motion of the particle as shown below in figure (1).

To determine

To find: The acceleration at time t and after 1 second.

Answer to Problem 3E

The acceleration at time is $\underset{\_}{\frac{-{\pi }^2}{4}\sin \frac{\pi t}{2}{\text{ft/s}}^2}$ and after one second is $\underset{\_}{-\frac{{\pi }^2}{4}{\text{ft/s}}^2}$.

Explanation of Solution

Calculate the acceleration at any time t.

Differentiate the equation (2) with respect to t.

$\begin{array}{c}a\left(t\right)=\frac{\pi }{2}\left(-\sin \frac{\pi t}{2}\times \frac{\pi }{2}\right)\\ =\frac{-{\pi }^2}{4}\sin \frac{\pi t}{2}\text{ft}/{\text{s}}^{\text{2}}\end{array}$

Therefore, the acceleration at any time is $\underset{\_}{\frac{-{\pi }^2}{4}\sin \frac{\pi t}{2}{\text{ft/s}}^2}$.

Calculate the acceleration after 1 second.

Substitute 1 for $t$ in the above equation $a\left(t\right)=\frac{\pi }{2}\left(-\sin \frac{\pi t}{2}\times \frac{\pi }{2}\right)$.

$\begin{array}{c}a\left(1\right)=\frac{-{\pi }^2}{4}\sin \frac{\pi \left(1\right)}{2}\text{ft}/{\text{s}}^{\text{2}}\\ =\frac{-{\pi }^2}{4}\text{ft}/{\text{s}}^{\text{2}}\end{array}$

Therefore, the acceleration after 1 second is $\underset{\_}{-\frac{{\pi }^2}{4}{\text{ft/s}}^2}$.

To determine

To sketch: The graph the position, velocity, and acceleration function for $0\le t\le 6$.

Answer to Problem 3E

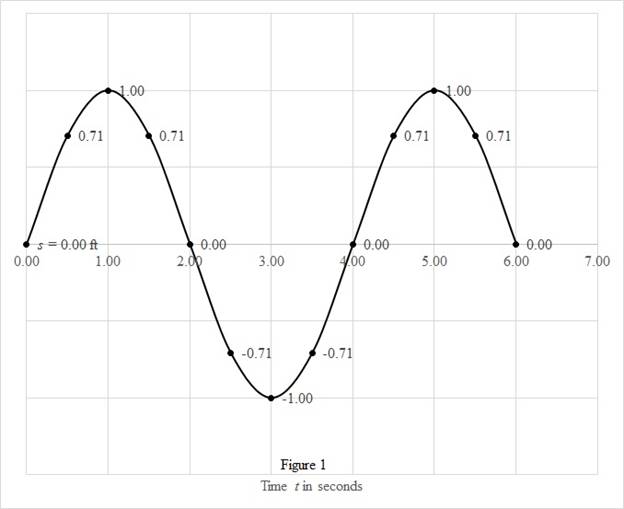
The position, velocity, and acceleration functions are plotted for time limits $0\le t\le 6$ in figures (2), (3), and (4).

Explanation of Solution

Calculate the position with respect to time using the formula.

$f\left(t\right)=\sin \frac{\pi t}{2}$

Substitute 0 for $t$ in the above equation.

$\begin{array}{c}f\left(t\right)=\sin \frac{\pi t}{2}\\ f\left(0\right)=\sin \frac{\pi \left(0\right)}{2}\\ =0\end{array}$

Similarly, calculate the remaining values.

Calculate the value of $t$ and $f\left(t\right)$ as shown in the table (1).

$t$	$f\left(t\right)=\sin \frac{\pi t}{2}$
0.00	0.00
0.50	0.71
1.00	1.00
1.50	0.71
2.00	0.00
2.50	-0.71
3.00	-1.00
3.50	-0.71
4.00	0.00
4.50	0.71
5.00	1.00
5.50	0.71
6.00	0.00

Calculate the velocity using the expression.

$v\left(t\right)=\frac{\pi }{2}\cos \frac{\pi t}{2}$

Substitute 0 for $t$ in the above equation.

$\begin{array}{c}v\left(0\right)=\frac{\pi }{2}\cos \frac{\pi \left(0\right)}{2}\\ =1.57\end{array}$

Similarly, calculate the remaining values.

Calculate the value of $t$ and $v\left(t\right)$ as shown in the table (2).

$t$	$v\left(t\right)=\frac{\pi }{2}\cos \frac{\pi t}{2}$
0.00	1.57
0.50	1.11
1.00	0.00
1.50	-1.11
2.00	-1.57
2.50	-1.11
3.00	0.00
3.50	1.11
4.00	1.57
4.50	1.11
5.00	0.00
5.50	-1.11
6.00	-1.57

Calculate the acceleration using the formula.

$a\left(t\right)=\frac{-{\pi }^2}{4}\sin \frac{\pi t}{2}$

Substitute 0 for $t$ in the above equation.

$\begin{array}{c}a\left(t\right)=\frac{-{\pi }^2}{4}\sin \frac{\pi t}{2}\\ a\left(0\right)=\frac{-{\pi }^2}{4}\sin \frac{\pi \left(0\right)}{2}\\ =0\end{array}$

Similarly, calculate the remaining values.

Calculate the value of $t$ and $a\left(t\right)$ as shown in the table (3).

$t$	$a\left(t\right)=\frac{-{\pi }^2}{4}\sin \frac{\pi t}{2}$
0.00	0.00
0.50	-1.74
1.00	-2.47
1.50	-1.74
2.00	0.00
2.50	1.74
3.00	2.47
3.50	1.74
4.00	0.00
4.50	-1.74
5.00	-2.47
5.50	-1.74
6.00	0.00

Draw the position as a function of time curve as shown in the Figure (2).

Draw the speed as a function of time curve as shown in the figure (3).

Draw the acceleration as a function of time curve as shown in the figure (4).

To determine

To find: The time when the particle is speeding up and slowing down.

Answer to Problem 3E

The acceleration is negative when the value of time is $0<t<2$ seconds and this will be slowing down and the acceleration is positive when the value of time is $2<t<4\sec$ and this will be speeding up. This cycle will repeat in the next 4 seconds, and go on.

Explanation of Solution

Calculate the time when particle speeding up and slowing down.

Substitute 0 for $f^{"}\left(t\right)$ in the equation $f^{"}\left(t\right)=\frac{-{\pi }^2}{4}\sin \frac{\pi t}{2}$.

$\begin{array}{l}0=\frac{-{\pi }^2}{4}\sin \frac{\pi t}{2}\\ \sin \frac{\pi t}{2}=0\\ t=0,2,4,\mathrm{...2}n\sec \end{array}$

Here, variable $n$ is given as natural numbers starting from 0.

Therefore, the acceleration is negative when the value of time is $0<t<2$ seconds and this will be slowing down and the acceleration is positive when the value of time is $2<t<4\sec$ and this will be speeding up. This cycle will repeat in the next 4 seconds, and go on.