
Elementary Geometry for College Students
6th Edition
ISBN: 9781285195698
Author: Daniel C. Alexander, Geralyn M. Koeberlein
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Textbook Question
Chapter 3.CT, Problem 18CT
Complete all missing statements and reasons in the following proof.
| Given: |
|
| Prove: |
|
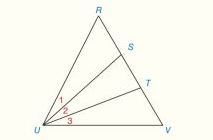
| Proof | |
| Statements | Reasons |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Expert Solution & Answer
Trending nowThis is a popular solution!

Chapter 3 Solutions
Elementary Geometry for College Students
Ch. 3.1 - In Exercises 1 to 4, consider the congruent...Ch. 3.1 - In Exercises 1 to 4. consider the congruent...Ch. 3.1 - In Exercises 1 to 4. consider the congruent...Ch. 3.1 - In Exercises 1 to 4, consider the congruent...Ch. 3.1 - Consider ABC and ABD in the figure shown. By the...Ch. 3.1 - In a right triangle, the sides that form the right...Ch. 3.1 - In ABC, the midpoints of the sides are joined. a...Ch. 3.1 - a. Suppose that you wish to prove that RSTSRV....Ch. 3.1 - In Exercises 9 to 12, congruent parts are...Ch. 3.1 - In Exercises 9 to 12, congruent parts are...
Ch. 3.1 - In Exercises 9 to 12, congruent parts are...Ch. 3.1 - In Exercises 9 to 12, congruent parts are...Ch. 3.1 - In Exercises 13 to 18, use only the given...Ch. 3.1 - In Exercises 13 to 18, use only the given...Ch. 3.1 - In Exercises 13 to 18, use only the given...Ch. 3.1 - In Exercises 13 to 18, use only the given...Ch. 3.1 - In Exercises 13 to 18, use only the given...Ch. 3.1 - In Exercises 13 to 18, use only the given...Ch. 3.1 - In Exercises 19 and 20, the triangles to be proved...Ch. 3.1 - In Exercises 19 and 20, the triangles to be proved...Ch. 3.1 - In Exercises 21 to 24, the triangles named can be...Ch. 3.1 - In Exercises 21 to 24, the triangles named can be...Ch. 3.1 - In Exercises 21 to 24, the triangles named can be...Ch. 3.1 - In Exercises 21 to 24, the triangles named can be...Ch. 3.1 - In Exercises 25 and 26, complete each proof. Use...Ch. 3.1 - In Exercises 25 and 26, complete each proof. Use...Ch. 3.1 - In Exercises 27 to 32, use SSS, SAS, ASA, or AAS...Ch. 3.1 - In Exercises 27 to 32, use SSS, SAS, ASA, or AAS...Ch. 3.1 - In Exercises 27 to 32, use SSS, SAS, ASA, or AAS...Ch. 3.1 - In Exercises 27 to 32, use SSS, SAS, ASA, or AAS...Ch. 3.1 - In Exercises 27 to 32, use SSS, SAS, ASA, or AAS...Ch. 3.1 - In Exercises 27 to 32, use SSS, SAS, ASA, or AAS...Ch. 3.1 - In Exercises 33 to 36, the methods to be used are...Ch. 3.1 - In Exercises 33 to 36, the methods to be used are...Ch. 3.1 - In Exercises 33 to 36, the method to be used are...Ch. 3.1 - In Exercises 33 to 36, the method to be used are...Ch. 3.1 - In quadrilateral ABCD, AC and BD are perpendicular...Ch. 3.1 - In ABC and DEF, you know that AD, CF, and ABDE....Ch. 3.1 - Prob. 39ECh. 3.1 - In Exercises 39 to 40, complete each proof. Given:...Ch. 3.1 - Given: ABC; RS is the perpendicular bisector of...Ch. 3.2 - In Exercises 1 to 4, state the reason SSS, SAS,...Ch. 3.2 - In Exercises 1 to 4, state the reason SSS, SAS,...Ch. 3.2 - In Exercises 1 to 4, state the reason SSS, SAS,...Ch. 3.2 - In Exercises 1 to 4, state the reason SSS, SAS,...Ch. 3.2 - In Exercise 5 to 12, plan and write the two-column...Ch. 3.2 - In Exercise 5 to 12, plan and write the two-column...Ch. 3.2 - In Exercise 5 to 12, plan and write the two-column...Ch. 3.2 - In Exercise 5 to 12, plan and write the two-column...Ch. 3.2 - Prob. 9ECh. 3.2 - In Exercise 5 to 12, plan and write the two-column...Ch. 3.2 - In Exercise 5 to 12, plan and write the two-column...Ch. 3.2 - In Exercise 5 to 12, plan and write the two-column...Ch. 3.2 - Prob. 13ECh. 3.2 - Prob. 14ECh. 3.2 - Given: HJ bisects KHL HJKL See figure for exercise...Ch. 3.2 - Given: HJ bisects KHL HJKL In Exercise 15, you cam...Ch. 3.2 - In Exercise 17 to 20, first prove that triangles...Ch. 3.2 - In Exercise 17 to 20, first prove that triangles...Ch. 3.2 - In Exercise 17 to 20, first prove that triangles...Ch. 3.2 - In Exercise 17 to 20, first prove that triangles...Ch. 3.2 - In Exercise 21 to 26, ABC is a right triangle. Use...Ch. 3.2 - In Exercise 21 to 26, ABC is a right triangle. Use...Ch. 3.2 - In Exercise 21 to 26, ABC is a right triangle. Use...Ch. 3.2 - In Exercise 21 to 26, ABC is a right triangle. Use...Ch. 3.2 - In Exercise 21 to 26, ABC is a right triangle. Use...Ch. 3.2 - In Exercise 21 to 26, ABC is a right triangle. Use...Ch. 3.2 - In Exercise 27 to 29, prove the indicated...Ch. 3.2 - In Exercise 27 to 29, prove the indicated...Ch. 3.2 - In Exercise 27 to 29, prove the indicated...Ch. 3.2 - Prob. 30ECh. 3.2 - Prob. 31ECh. 3.2 - In Exercises 30 to 32, draw the triangles that are...Ch. 3.2 - Given: RW bisects SRU Prove: RSRU TRUVRS HINT:...Ch. 3.2 - Given: DBBC and CEDE Prove: ABAE BDCECD HINT:...Ch. 3.2 - In the roof truss shown, AB=8 and mHAF=37. Find: a...Ch. 3.2 - In the support system of the bridge shown, AC=6ft...Ch. 3.2 - As a car moves along the roadway in a mountain...Ch. 3.2 - Because of the construction along the road from A...Ch. 3.2 - Given: Regular pentagon ABCDE with diagonals BE...Ch. 3.2 - In the figure with regular pentagon ABCDE, do BE...Ch. 3.3 - For Exercises 1 to 8, use the accompanying...Ch. 3.3 - Prob. 2ECh. 3.3 - Prob. 3ECh. 3.3 - Prob. 4ECh. 3.3 - Prob. 5ECh. 3.3 - For Exercises 1 to 8, use the accompanying...Ch. 3.3 - Prob. 7ECh. 3.3 - Prob. 8ECh. 3.3 - In Exercises 9 to 12, determine whether the sets...Ch. 3.3 - Prob. 10ECh. 3.3 - In Exercises 9 to 12, determine whether the sets...Ch. 3.3 - In Exercises 9 to 12, determine whether the sets...Ch. 3.3 - In Exercises 13 to 18, describe the line segments...Ch. 3.3 - Prob. 14ECh. 3.3 - In Exercises 13 to 18, describe the line segments...Ch. 3.3 - In Exercises 13 to 18, describe the line segments...Ch. 3.3 - In Exercises 13 to 18, describe the line segments...Ch. 3.3 - Prob. 18ECh. 3.3 - Prob. 19ECh. 3.3 - Is it possible for a triangle to be: a an acute...Ch. 3.3 - Prob. 21ECh. 3.3 - In concave quadrilateral ABCD, the angle at A...Ch. 3.3 - Prob. 23ECh. 3.3 - Prob. 24ECh. 3.3 - Prob. 25ECh. 3.3 - Prob. 26ECh. 3.3 - Prob. 27ECh. 3.3 - Prob. 28ECh. 3.3 - Prob. 29ECh. 3.3 - Prob. 30ECh. 3.3 - Prob. 31ECh. 3.3 - Prob. 32ECh. 3.3 - Suppose that ABCDEF. Also, AX bisects CAB and DY...Ch. 3.3 - Suppose that ABCDEF. Also, AX is the median from A...Ch. 3.3 - In Exercises 35 and 36, complete each proof using...Ch. 3.3 - Prob. 36ECh. 3.3 - Prob. 37ECh. 3.3 - Prob. 38ECh. 3.3 - Prob. 39ECh. 3.3 - In isosceles triangle BAT, ABAT.Also, BRBTAR, if...Ch. 3.3 - Prob. 41ECh. 3.3 - Prob. 42ECh. 3.3 - Prob. 43ECh. 3.3 - Prob. 44ECh. 3.3 - Prob. 45ECh. 3.3 - Prob. 46ECh. 3.3 - Given: In the figure, XZYZ and Z is the midpoint...Ch. 3.3 - Prob. 48ECh. 3.4 - In Exercises 1 to 6, use line segments of given...Ch. 3.4 - Prob. 2ECh. 3.4 - Prob. 3ECh. 3.4 - Prob. 4ECh. 3.4 - Prob. 5ECh. 3.4 - Prob. 6ECh. 3.4 - Prob. 7ECh. 3.4 - Prob. 8ECh. 3.4 - Prob. 9ECh. 3.4 - Prob. 10ECh. 3.4 - Prob. 11ECh. 3.4 - Prob. 12ECh. 3.4 - In Exercises 13 and 14. use the angles and lengths...Ch. 3.4 - Prob. 14ECh. 3.4 - Prob. 15ECh. 3.4 - Prob. 16ECh. 3.4 - Prob. 17ECh. 3.4 - Prob. 18ECh. 3.4 - Prob. 19ECh. 3.4 - Prob. 20ECh. 3.4 - Prob. 21ECh. 3.4 - Prob. 22ECh. 3.4 - In Exercises 23 to 26, use line segments of length...Ch. 3.4 - Prob. 24ECh. 3.4 - In Exercises 23 to 26, use line segments of length...Ch. 3.4 - Prob. 26ECh. 3.4 - In Exercise 27 and 28, use the given angle R and...Ch. 3.4 - Prob. 28ECh. 3.4 - Complete the justification of the construction of...Ch. 3.4 - Prob. 30ECh. 3.4 - Prob. 31ECh. 3.4 - Prob. 32ECh. 3.4 - Prob. 33ECh. 3.4 - Prob. 34ECh. 3.4 - Prob. 35ECh. 3.4 - Draw a right triangle and construct the angle...Ch. 3.4 - Draw an obtuse triangle and construct the three...Ch. 3.4 - Prob. 38ECh. 3.4 - A carpenter has placed a square over an angle in...Ch. 3.4 - Prob. 40ECh. 3.5 - In Exercise 1 to 10, classify each statement as...Ch. 3.5 - In Exercise 1 to 10, classify each statement as...Ch. 3.5 - In Exercise 1 to 10, classify each statement as...Ch. 3.5 - In Exercise 1 to 10, classify each statement as...Ch. 3.5 - In Exercise 1 to 10, classify each statement as...Ch. 3.5 - In Exercise 1 to 10, classify each statement as...Ch. 3.5 - In Exercise 1 to 10, classify each statement as...Ch. 3.5 - In Exercise 1 to 10, classify each statement as...Ch. 3.5 - In Exercise 1 to 10, classify each statement as...Ch. 3.5 - In Exercise 1 to 10, classify each statement as...Ch. 3.5 - Is it possible to draw a triangle whose angles...Ch. 3.5 - Is it possible to draw a triangle whose angles...Ch. 3.5 - Is it possible to draw a triangle whose sides...Ch. 3.5 - Is it possible to draw a triangle whose sides...Ch. 3.5 - Prob. 15ECh. 3.5 - In Exercises 15 to 18, describe the triangle XYZ ,...Ch. 3.5 - Prob. 17ECh. 3.5 - In Exercises 15 to 18, describe the triangle XYZ ,...Ch. 3.5 - Two of the sides of an isosceles triangle have...Ch. 3.5 - The sides of a right triangle have lengths of 6cm,...Ch. 3.5 - Prob. 21ECh. 3.5 - One of the angles of an isosceles triangle...Ch. 3.5 - Prob. 23ECh. 3.5 - A tornado has just struck a small Kansas community...Ch. 3.5 - In Exercises 25 and 26, complete each proof shown...Ch. 3.5 - Prob. 26ECh. 3.5 - In Exercises 27 and 28, construct proofs. Given:...Ch. 3.5 - In Exercises 27 and 28, construct proofs. Given:...Ch. 3.5 - Prob. 29ECh. 3.5 - In MNP not shown, point Q lies on NP so that MQ...Ch. 3.5 - In Exercises 31 to 34, apply a form of Theorem...Ch. 3.5 - In Exercises 31 to 34, apply a form of Theorem...Ch. 3.5 - Prob. 33ECh. 3.5 - In Exercises 31 to 34, apply a form of Theorem...Ch. 3.5 - Prove by the indirect method: Given: MPN is not...Ch. 3.5 - Prove by the indirect method: Given: Scalene XYZ...Ch. 3.5 - In Exercises 37 and 38, prove each theorem. The...Ch. 3.5 - In Exercises 37 and 38, prove each theorem. The...Ch. 3.CR - Given: AEBDEC AEDE Prove: AEBDECCh. 3.CR - Given: ABEFACDF12 Prove: BECh. 3.CR - Given: AD bisects BC ABBCDCBC Prove: AEDECh. 3.CR - Prob. 4CRCh. 3.CR - Prob. 5CRCh. 3.CR - Given: B is the midpoint of AC BDAC Prove: ADC is...Ch. 3.CR - Prob. 7CRCh. 3.CR - Prob. 8CRCh. 3.CR - Given: YZ is the base of an isosceles triangle;...Ch. 3.CR - Prob. 10CRCh. 3.CR - Prob. 11CRCh. 3.CR - Prob. 12CRCh. 3.CR - Prob. 13CRCh. 3.CR - Given: AC bisects BAD Prove: ADCDCh. 3.CR - Prob. 15CRCh. 3.CR - Prob. 16CRCh. 3.CR - Prob. 17CRCh. 3.CR - Name the longest line segment shown in...Ch. 3.CR - Prob. 19CRCh. 3.CR - Two sides of a triangle have lengths 15 and 20....Ch. 3.CR - Prob. 21CRCh. 3.CR - Prob. 22CRCh. 3.CR - Prob. 23CRCh. 3.CR - Prob. 24CRCh. 3.CR - Given: ABC is isosceles with base AB...Ch. 3.CR - Prob. 26CRCh. 3.CR - Prob. 27CRCh. 3.CR - Construct a right triangle that has acute angle A...Ch. 3.CR - Construct a second isosceles triangle in which the...Ch. 3.CT - It is given that ABCDEF triangles not shown a If...Ch. 3.CT - Consider XYZ triangles not shown a Which side is...Ch. 3.CT - Prob. 3CTCh. 3.CT - Prob. 4CTCh. 3.CT - With congruent parts marked, are the two triangles...Ch. 3.CT - Prob. 6CTCh. 3.CT - Prob. 7CTCh. 3.CT - CM is the median for ABC from vertex C to side AB....Ch. 3.CT - Prob. 9CTCh. 3.CT - Prob. 10CTCh. 3.CT - Prob. 11CTCh. 3.CT - Show all arcs in the following construction....Ch. 3.CT - Prob. 13CTCh. 3.CT - Prob. 14CTCh. 3.CT - Prob. 15CTCh. 3.CT - Prob. 16CTCh. 3.CT - Complete all statements and reasons for the...Ch. 3.CT - Complete all missing statements and reasons in the...Ch. 3.CT - The perimeter of an isosceles triangle is 32cm. If...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, geometry and related others by exploring similar questions and additional content below.Similar questions
- Given: rs Transversal t 1 is a right Prove: 2 is a rightarrow_forwardHA hypotenuse-angle is also a valid method for proving that two right triangles are congruent a Given that AD and ABDE in the right triangles shown, can HA be used to verify that ABCDEF? b Name another method SSS, SAS. etc. that can be used to verify that these triangles are congruent.arrow_forwardGiven: Equiangular RST Prove: RV bisects SRT RVS is a rightarrow_forward
- Use a two-column proof to prove the following theorem: The lengths of the corresponding altitudes of similar triangles have the same ratio as lengths of any pair of corresponding sides. Given: DEFMNP; DG and MQ are altitudes Prove: DGMQ=DEMNarrow_forwarda. Suppose that you wish to prove that RSTSRV. Using the reason Identity, name one pair of corresponding parts that are congruent. b. Suppose you wish to prove that RWTSWV. Considering the figure, name one pair of corresponding angles of these triangles that must be congruent.arrow_forwardIn right ABC with right C,AD bisects BAC. If AC=6 and DC=3, find BD and AB. HINT: Let BD=x and AB=2x. Then use the Pythagorean Theorem.arrow_forward
- Prove the Extended Angle Addition Property by using the Drawing, the Given, and the Prove that follow. Given: TSW with SU and SV Prove: mTSW=mTSU+mUSV+mVSWarrow_forwardConsider regular pentagon RSTVQ not shown. Given that diagonals QT and VR intersect at point F, show that VFFR=TFFQ.arrow_forwardComplete the proof of the following theorem: In a kite, one pair of opposite angles are congruent. Given: Kite ABCD; ABADandBCDC Prove: BD PROOF Statements Reasons 1_________ 2. Draw AC 3.__________ 4. ACDACB 5.__________ 1.______________ 2. Through two points, there is exactly one line. 3. Identity 4.____________ 5._________________arrow_forward
- Complete an analytic proof of the following theorem: In a triangle that has sides of lengths a,b, and c, if c2=a2+b2, then the triangle is a right triangle.arrow_forwardIn Exercises 27 to 30, fill in the missing reasons for each geometric proof. Given: E is the midpoint of DF Prove: DE=12(DF) Exercises 27, 28 PROOF Statements Reasons 1. E is the midpoint of DF 1. ? 2. DE=EF 2. ? 3. DE+EF=DF 3. ? 4. DE+DE=DF 4. ? 5. 2(DE)=DF 5. ? 6. DE=12(DF) 6. ?arrow_forwardIn ABC and DEF, you know that AD, CF, and ABDE. Before concluding that the triangles are congruent by ASA, you need to show that BE. State the postulate or theorem that allows you to confirm this statement (BE).arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
 Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage, Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning
Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
 Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,

Elementary Geometry For College Students, 7e
Geometry
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Cengage,

Elementary Geometry for College Students
Geometry
ISBN:9781285195698
Author:Daniel C. Alexander, Geralyn M. Koeberlein
Publisher:Cengage Learning

Holt Mcdougal Larson Pre-algebra: Student Edition...
Algebra
ISBN:9780547587776
Author:HOLT MCDOUGAL
Publisher:HOLT MCDOUGAL

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,
What are the Different Types of Triangles? | Don't Memorise; Author: Don't Memorise;https://www.youtube.com/watch?v=1k0G-Y41jRA;License: Standard YouTube License, CC-BY
Law of Sines AAS, ASA, SSA Ambiguous Case; Author: Mario's Math Tutoring;https://www.youtube.com/watch?v=FPVGb-yWj3s;License: Standard YouTube License, CC-BY
Introduction to Statistics..What are they? And, How Do I Know Which One to Choose?; Author: The Doctoral Journey;https://www.youtube.com/watch?v=HpyRybBEDQ0;License: Standard YouTube License, CC-BY
Triangles | Mathematics Grade 5 | Periwinkle; Author: Periwinkle;https://www.youtube.com/watch?v=zneP1Q7IjgQ;License: Standard YouTube License, CC-BY
What Are Descriptive Statistics And Inferential Statistics?; Author: Amour Learning;https://www.youtube.com/watch?v=MUyUaouisZE;License: Standard Youtube License