
Single Variable Calculus: Early Transcendentals, Volume I
8th Edition
ISBN: 9781305270343
Author: James Stewart
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Concept explainers
Textbook Question
Chapter 4, Problem 20P
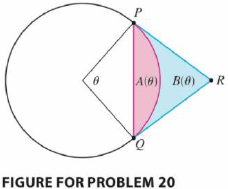
An arc PQ of a circle subtends a central angle θ as in the figure. Let A(θ) be the area between the chord PQ and the arc PQ. Let B(θ) be the area between the tangent lines PR, QR, and the arc. Find
Expert Solution & Answer
Trending nowThis is a popular solution!

Students have asked these similar questions
Find the length of the arc of the parabola y sq = x from ( 0, 0 ) to ( 1,1)
Let L be the tangent line to the parabola y=x2+3 at the point (1, 4). The angle of inclination of L is the angle PHI that L makes with the positive direction of the x axis. Calculate PHI to the nearest degree.
Find the length of the arc of the parabola y sq = x cu . from ( 0, 0 ) to ( 1,1)
Chapter 4 Solutions
Single Variable Calculus: Early Transcendentals, Volume I
Ch. 4.1 - Explain the difference between an absolute minimum...Ch. 4.1 - Prob. 2ECh. 4.1 - Prob. 3ECh. 4.1 - Prob. 4ECh. 4.1 - Use the graph to state the absolute and local...Ch. 4.1 - Use the graph to state the absolute and local...Ch. 4.1 - Sketch the graph of a function f that is...Ch. 4.1 - Sketch the graph of a function f that is...Ch. 4.1 - Prob. 9ECh. 4.1 - Prob. 10E
Ch. 4.1 - (a) Sketch the graph of a function that has a...Ch. 4.1 - (a) Sketch the graph of a function on [1, 2] that...Ch. 4.1 - (a) Sketch the graph of a function on [1, 2] that...Ch. 4.1 - (a) Sketch the graph of a function that has two...Ch. 4.1 - Sketch the graph of f by hand and use your sketch...Ch. 4.1 - Prob. 16ECh. 4.1 - Prob. 17ECh. 4.1 - Prob. 18ECh. 4.1 - Prob. 19ECh. 4.1 - Prob. 20ECh. 4.1 - Prob. 21ECh. 4.1 - Prob. 22ECh. 4.1 - Prob. 23ECh. 4.1 - Prob. 24ECh. 4.1 - Prob. 25ECh. 4.1 - Prob. 26ECh. 4.1 - Prob. 27ECh. 4.1 - Prob. 28ECh. 4.1 - Prob. 29ECh. 4.1 - Prob. 30ECh. 4.1 - Prob. 31ECh. 4.1 - Prob. 32ECh. 4.1 - Prob. 33ECh. 4.1 - Prob. 34ECh. 4.1 - Prob. 35ECh. 4.1 - Prob. 36ECh. 4.1 - Prob. 37ECh. 4.1 - Prob. 38ECh. 4.1 - Prob. 39ECh. 4.1 - Prob. 40ECh. 4.1 - Prob. 41ECh. 4.1 - Prob. 42ECh. 4.1 - Prob. 43ECh. 4.1 - Prob. 44ECh. 4.1 - A formula for the derivative of a function f is...Ch. 4.1 - A formula for the derivative of a function f is...Ch. 4.1 - Find the absolute maximum and absolute minimum...Ch. 4.1 - Find the absolute maximum and absolute minimum...Ch. 4.1 - Find the absolute maximum and absolute minimum...Ch. 4.1 - Find the absolute maximum and absolute minimum...Ch. 4.1 - Find the absolute maximum and absolute minimum...Ch. 4.1 - Find the absolute maximum and absolute minimum...Ch. 4.1 - Find the absolute maximum and absolute minimum...Ch. 4.1 - Find the absolute maximum and absolute minimum...Ch. 4.1 - Find the absolute maximum and absolute minimum...Ch. 4.1 - Find the absolute maximum and absolute minimum...Ch. 4.1 - Find the absolute maximum and absolute minimum...Ch. 4.1 - Find the absolute maximum and absolute minimum...Ch. 4.1 - Find the absolute maximum and absolute minimum...Ch. 4.1 - Find the absolute maximum and absolute minimum...Ch. 4.1 - Find the absolute maximum and absolute minimum...Ch. 4.1 - Find the absolute maximum and absolute minimum...Ch. 4.1 - If a and b are positive numbers, find the maximum...Ch. 4.1 - Use a graph to estimate the critical numbers of...Ch. 4.1 - Prob. 65ECh. 4.1 - (a) Use a graph to estimate the absolute maximum...Ch. 4.1 - (a) Use a graph to estimate the absolute maximum...Ch. 4.1 - (a) Use a graph to estimate the absolute maximum...Ch. 4.1 - After the consumption of an alcoholic beverage,...Ch. 4.1 - After an antibiotic tablet is taken, the...Ch. 4.1 - Between 0C and 30C, the volume V (in cubic...Ch. 4.1 - An object with weight W is dragged along a...Ch. 4.1 - The water level, measured in feet above mean sea...Ch. 4.1 - On May 7, 1992, the space shuttle Endeavour was...Ch. 4.1 - Prob. 75ECh. 4.1 - Prob. 76ECh. 4.1 - Prob. 77ECh. 4.1 - Prob. 78ECh. 4.1 - Prob. 79ECh. 4.1 - A cubic function is a polynomial of degree 3; that...Ch. 4.2 - The graph of a function f is shown. Verify that f...Ch. 4.2 - Draw the graph of a function defined on [0, 8]...Ch. 4.2 - The graph of a function g is shown. (a) Verify...Ch. 4.2 - Draw the graph of a function that is continuous on...Ch. 4.2 - Verify that the function satisfies the three...Ch. 4.2 - Verify that the function satisfies the three...Ch. 4.2 - Verify that the function satisfies the three...Ch. 4.2 - Verify that the function satisfies the three...Ch. 4.2 - Let f(x) = 1 x2/3. Show that f(l) = f(1) but...Ch. 4.2 - Let f(x) = tan x. Show that f(0) = f() but there...Ch. 4.2 - Verify that the function satisfies the hypotheses...Ch. 4.2 - Verify that the function satisfies the hypotheses...Ch. 4.2 - Verify that the function satisfies the hypotheses...Ch. 4.2 - Verify that the function satisfies the hypotheses...Ch. 4.2 - Find the number c that satisfies the conclusion of...Ch. 4.2 - Find the number c that satisfies the conclusion of...Ch. 4.2 - Let f(x) = (x 3)2. Show that there is no value of...Ch. 4.2 - Let f(x) = 2 |2x 1|. Show that there is no value...Ch. 4.2 - Show that the equation has exactly one real root....Ch. 4.2 - Show that the equation has exactly one real root....Ch. 4.2 - Show that the equation x3 15x + c = 0 has at most...Ch. 4.2 - Show that the equation x4 + 4x + c = 0 has at most...Ch. 4.2 - (a) Show that a polynomial of degree 3 has at most...Ch. 4.2 - Prob. 24ECh. 4.2 - Prob. 25ECh. 4.2 - Prob. 26ECh. 4.2 - Does there exist a function f such that f(0) = 1,...Ch. 4.2 - Prob. 28ECh. 4.2 - Show that sin x x if 0 x 2.Ch. 4.2 - Prob. 30ECh. 4.2 - Prob. 31ECh. 4.2 - If f(x) = c (c a constant) for all x, use...Ch. 4.2 - Prob. 33ECh. 4.2 - Use the method of Example 6 to prove the identity...Ch. 4.2 - Prob. 36ECh. 4.2 - Prob. 37ECh. 4.2 - A number a is called a fixed point of a function f...Ch. 4.3 - Use the given graph of f to find the following....Ch. 4.3 - Prob. 2ECh. 4.3 - Prob. 3ECh. 4.3 - Prob. 4ECh. 4.3 - The graph of the derivative f of a function f is...Ch. 4.3 - The graph of the derivative f of a function f is...Ch. 4.3 - In each part state the x-coordinates of the...Ch. 4.3 - The graph of the first derivative f of a function...Ch. 4.3 - (a) Find the intervals on which f is increasing or...Ch. 4.3 - Prob. 10ECh. 4.3 - Prob. 11ECh. 4.3 - (a) Find the intervals on which f is increasing or...Ch. 4.3 - Prob. 13ECh. 4.3 - Prob. 14ECh. 4.3 - Prob. 15ECh. 4.3 - Prob. 16ECh. 4.3 - Prob. 17ECh. 4.3 - Prob. 18ECh. 4.3 - Prob. 19ECh. 4.3 - Prob. 20ECh. 4.3 - Prob. 21ECh. 4.3 - Prob. 22ECh. 4.3 - Prob. 23ECh. 4.3 - Prob. 24ECh. 4.3 - Prob. 25ECh. 4.3 - Prob. 26ECh. 4.3 - Prob. 27ECh. 4.3 - Prob. 28ECh. 4.3 - Prob. 29ECh. 4.3 - Prob. 30ECh. 4.3 - Sketch the graph of a function that satisfies all...Ch. 4.3 - Prob. 32ECh. 4.3 - Suppose f is a continuous function where f(x) 0...Ch. 4.3 - The graph of a function y = f(x) is shown. At...Ch. 4.3 - The graph of the derivative f of a continuous...Ch. 4.3 - The graph of the derivative f of a continuous...Ch. 4.3 - (a) Find the intervals of increase or decrease....Ch. 4.3 - (a) Find the intervals of increase or decrease....Ch. 4.3 - (a) Find the intervals of increase or decrease....Ch. 4.3 - (a) Find the intervals of increase or decrease....Ch. 4.3 - (a) Find the intervals of increase or decrease....Ch. 4.3 - (a) Find the intervals of increase or decrease....Ch. 4.3 - (a) Find the intervals of increase or decrease....Ch. 4.3 - (a) Find the intervals of increase or decrease....Ch. 4.3 - (a) Find the intervals of increase or decrease....Ch. 4.3 - (a) Find the intervals of increase or decrease....Ch. 4.3 - (a) Find the intervals of increase or decrease....Ch. 4.3 - (a) Find the intervals of increase or decrease....Ch. 4.3 - (a) Find the vertical and horizontal asymptotes....Ch. 4.3 - (a) Find the vertical and horizontal asymptotes....Ch. 4.3 - Prob. 51ECh. 4.3 - (a) Find the vertical and horizontal asymptotes....Ch. 4.3 - Prob. 53ECh. 4.3 - Prob. 54ECh. 4.3 - Prob. 55ECh. 4.3 - Prob. 56ECh. 4.3 - Prob. 57ECh. 4.3 - Prob. 58ECh. 4.3 - Prob. 59ECh. 4.3 - Prob. 60ECh. 4.3 - Prob. 61ECh. 4.3 - Prob. 62ECh. 4.3 - In an episode of The Simpsons television show,...Ch. 4.3 - Prob. 67ECh. 4.3 - Prob. 68ECh. 4.3 - Prob. 69ECh. 4.3 - Prob. 70ECh. 4.3 - Prob. 71ECh. 4.3 - Prob. 72ECh. 4.3 - Find a cubic function f(x) = ax3 + bx2 + cx + d...Ch. 4.3 - Prob. 74ECh. 4.3 - Prob. 75ECh. 4.3 - Prob. 76ECh. 4.3 - Prob. 77ECh. 4.3 - Prob. 78ECh. 4.3 - Prob. 79ECh. 4.3 - Prob. 80ECh. 4.3 - Prob. 81ECh. 4.3 - Prob. 82ECh. 4.3 - Prob. 83ECh. 4.3 - Prob. 84ECh. 4.3 - Prob. 85ECh. 4.3 - Prob. 86ECh. 4.3 - Prob. 87ECh. 4.3 - Prob. 88ECh. 4.3 - Prob. 89ECh. 4.3 - Prob. 90ECh. 4.3 - Prob. 92ECh. 4.3 - Prob. 93ECh. 4.4 - Given that...Ch. 4.4 - Prob. 2ECh. 4.4 - Prob. 3ECh. 4.4 - Prob. 4ECh. 4.4 - Use the graphs of f and g and their tangent lines...Ch. 4.4 - Use the graphs of f and g and their tangent lines...Ch. 4.4 - The graph of a function f and its tangent line at...Ch. 4.4 - Prob. 8ECh. 4.4 - Prob. 9ECh. 4.4 - Prob. 10ECh. 4.4 - Prob. 11ECh. 4.4 - Prob. 12ECh. 4.4 - Prob. 13ECh. 4.4 - Prob. 14ECh. 4.4 - Prob. 15ECh. 4.4 - Prob. 16ECh. 4.4 - Prob. 17ECh. 4.4 - Prob. 18ECh. 4.4 - Prob. 19ECh. 4.4 - Prob. 20ECh. 4.4 - Find the limit. Use lHospitals Rule where...Ch. 4.4 - Prob. 22ECh. 4.4 - Prob. 23ECh. 4.4 - Prob. 24ECh. 4.4 - Find the limit. Use lHospitals Rule where...Ch. 4.4 - Find the limit. Use lHospitals Rule where...Ch. 4.4 - Prob. 27ECh. 4.4 - Prob. 28ECh. 4.4 - Prob. 29ECh. 4.4 - Prob. 30ECh. 4.4 - Prob. 31ECh. 4.4 - Prob. 32ECh. 4.4 - Prob. 33ECh. 4.4 - Prob. 34ECh. 4.4 - Prob. 35ECh. 4.4 - Prob. 36ECh. 4.4 - Prob. 37ECh. 4.4 - Prob. 38ECh. 4.4 - Prob. 39ECh. 4.4 - Prob. 40ECh. 4.4 - Prob. 41ECh. 4.4 - Prob. 42ECh. 4.4 - Prob. 43ECh. 4.4 - Prob. 44ECh. 4.4 - Prob. 45ECh. 4.4 - Prob. 46ECh. 4.4 - Prob. 47ECh. 4.4 - Prob. 48ECh. 4.4 - Prob. 49ECh. 4.4 - Prob. 50ECh. 4.4 - Prob. 51ECh. 4.4 - Find the limit. Use lHospitals Rule where...Ch. 4.4 - Prob. 53ECh. 4.4 - Find the limit. Use lHospitals Rule where...Ch. 4.4 - Find the limit. Use lHospitals Rule where...Ch. 4.4 - Find the limit. Use lHospitals Rule where...Ch. 4.4 - Find the limit. Use lHospitals Rule where...Ch. 4.4 - Find the limit. Use lHospitals Rule where...Ch. 4.4 - Prob. 59ECh. 4.4 - Prob. 60ECh. 4.4 - Prob. 61ECh. 4.4 - Prob. 62ECh. 4.4 - Prob. 63ECh. 4.4 - Prob. 64ECh. 4.4 - Prob. 65ECh. 4.4 - Prob. 66ECh. 4.4 - Prob. 67ECh. 4.4 - Prob. 68ECh. 4.4 - Prob. 69ECh. 4.4 - Prob. 70ECh. 4.4 - Prob. 71ECh. 4.4 - Prob. 72ECh. 4.4 - Prob. 73ECh. 4.4 - Prob. 74ECh. 4.4 - Prob. 75ECh. 4.4 - Prob. 76ECh. 4.4 - Prob. 77ECh. 4.4 - Prob. 78ECh. 4.4 - If an initial amount A0 of money is invested at an...Ch. 4.4 - Prob. 80ECh. 4.4 - Prob. 81ECh. 4.4 - Prob. 82ECh. 4.4 - Prob. 83ECh. 4.4 - Prob. 84ECh. 4.4 - Prob. 85ECh. 4.4 - Prob. 86ECh. 4.4 - Prob. 87ECh. 4.4 - Prob. 88ECh. 4.4 - Prob. 89ECh. 4.4 - Prob. 90ECh. 4.4 - Prob. 91ECh. 4.4 - Prob. 92ECh. 4.5 - Use the guidelines of this section to sketch the...Ch. 4.5 - Prob. 2ECh. 4.5 - Prob. 3ECh. 4.5 - Prob. 4ECh. 4.5 - Prob. 5ECh. 4.5 - Prob. 6ECh. 4.5 - Prob. 7ECh. 4.5 - Prob. 8ECh. 4.5 - Prob. 9ECh. 4.5 - Use the guidelines of this section to sketch the...Ch. 4.5 - Prob. 11ECh. 4.5 - Use the guidelines of this section to sketch the...Ch. 4.5 - Prob. 13ECh. 4.5 - Prob. 14ECh. 4.5 - Prob. 15ECh. 4.5 - Prob. 16ECh. 4.5 - Prob. 17ECh. 4.5 - Prob. 18ECh. 4.5 - Prob. 19ECh. 4.5 - Prob. 20ECh. 4.5 - Prob. 21ECh. 4.5 - Prob. 22ECh. 4.5 - Prob. 23ECh. 4.5 - Prob. 24ECh. 4.5 - Prob. 25ECh. 4.5 - Prob. 26ECh. 4.5 - Prob. 27ECh. 4.5 - Prob. 28ECh. 4.5 - Prob. 29ECh. 4.5 - Prob. 30ECh. 4.5 - Prob. 31ECh. 4.5 - Prob. 32ECh. 4.5 - Prob. 33ECh. 4.5 - Prob. 34ECh. 4.5 - Prob. 35ECh. 4.5 - Prob. 36ECh. 4.5 - Prob. 37ECh. 4.5 - Prob. 38ECh. 4.5 - Prob. 39ECh. 4.5 - Prob. 40ECh. 4.5 - Prob. 41ECh. 4.5 - Prob. 42ECh. 4.5 - Prob. 43ECh. 4.5 - Prob. 44ECh. 4.5 - Prob. 45ECh. 4.5 - Prob. 46ECh. 4.5 - Prob. 47ECh. 4.5 - Prob. 48ECh. 4.5 - Prob. 49ECh. 4.5 - Prob. 50ECh. 4.5 - Prob. 51ECh. 4.5 - Prob. 52ECh. 4.5 - Prob. 53ECh. 4.5 - Prob. 54ECh. 4.5 - Prob. 55ECh. 4.5 - Prob. 56ECh. 4.5 - Prob. 57ECh. 4.5 - A model for the concentration at time t of a drug...Ch. 4.5 - Prob. 59ECh. 4.5 - Prob. 60ECh. 4.5 - Prob. 61ECh. 4.5 - Prob. 62ECh. 4.5 - Prob. 63ECh. 4.5 - Prob. 64ECh. 4.5 - Use the guidelines of this section to sketch the...Ch. 4.5 - Prob. 66ECh. 4.5 - Prob. 67ECh. 4.5 - Prob. 68ECh. 4.5 - Prob. 69ECh. 4.5 - Use the guidelines of this section to sketch the...Ch. 4.5 - Prob. 71ECh. 4.5 - Prob. 72ECh. 4.5 - Prob. 73ECh. 4.5 - Prob. 74ECh. 4.5 - Prob. 75ECh. 4.5 - Prob. 76ECh. 4.6 - Prob. 1ECh. 4.6 - Prob. 2ECh. 4.6 - Prob. 3ECh. 4.6 - Prob. 4ECh. 4.6 - Prob. 5ECh. 4.6 - Prob. 6ECh. 4.6 - Prob. 9ECh. 4.6 - Prob. 10ECh. 4.6 - Prob. 13ECh. 4.6 - Prob. 14ECh. 4.6 - Prob. 27ECh. 4.6 - Prob. 28ECh. 4.6 - Prob. 29ECh. 4.6 - Prob. 30ECh. 4.6 - Prob. 33ECh. 4.6 - Prob. 34ECh. 4.6 - Prob. 35ECh. 4.6 - Prob. 38ECh. 4.6 - Prob. 39ECh. 4.6 - Prob. 40ECh. 4.7 - Consider the following problem: Find two numbers...Ch. 4.7 - Find two numbers whose difference is 100 and whose...Ch. 4.7 - Prob. 3ECh. 4.7 - The sum of two positive numbers is 16. What is the...Ch. 4.7 - What is the maximum vertical distance between the...Ch. 4.7 - Prob. 6ECh. 4.7 - Prob. 7ECh. 4.7 - Prob. 8ECh. 4.7 - Prob. 9ECh. 4.7 - Prob. 10ECh. 4.7 - Prob. 11ECh. 4.7 - Prob. 12ECh. 4.7 - Prob. 13ECh. 4.7 - Prob. 14ECh. 4.7 - Prob. 15ECh. 4.7 - Prob. 16ECh. 4.7 - Prob. 17ECh. 4.7 - A farmer wants to fence in a rectangular plot of...Ch. 4.7 - Prob. 19ECh. 4.7 - Prob. 20ECh. 4.7 - Prob. 21ECh. 4.7 - Prob. 22ECh. 4.7 - Prob. 23ECh. 4.7 - Prob. 24ECh. 4.7 - Prob. 25ECh. 4.7 - Prob. 26ECh. 4.7 - Prob. 27ECh. 4.7 - Prob. 28ECh. 4.7 - Prob. 29ECh. 4.7 - Prob. 30ECh. 4.7 - Prob. 31ECh. 4.7 - Prob. 32ECh. 4.7 - Prob. 33ECh. 4.7 - A Norman window has the shape of a rectangle...Ch. 4.7 - Prob. 35ECh. 4.7 - A poster is to have an area of 180 in2 with 1-inch...Ch. 4.7 - Prob. 37ECh. 4.7 - Prob. 38ECh. 4.7 - If you are offered one slice from a round pizza...Ch. 4.7 - Prob. 40ECh. 4.7 - A cone-shaped drinking cup is made from a circular...Ch. 4.7 - Prob. 42ECh. 4.7 - Prob. 43ECh. 4.7 - Prob. 44ECh. 4.7 - Prob. 45ECh. 4.7 - For a fish swimming at a speed v relative to the...Ch. 4.7 - Prob. 47ECh. 4.7 - A boat leaves a dock at 2:00 pm and travels due...Ch. 4.7 - Prob. 49ECh. 4.7 - Prob. 50ECh. 4.7 - An oil refinery is located on the north bank of a...Ch. 4.7 - Prob. 52ECh. 4.7 - Prob. 53ECh. 4.7 - Prob. 54ECh. 4.7 - Prob. 55ECh. 4.7 - At which points on the curve y = 1 + 40x3 3x5...Ch. 4.7 - Prob. 57ECh. 4.7 - Prob. 58ECh. 4.7 - Prob. 59ECh. 4.7 - Prob. 60ECh. 4.7 - Prob. 61ECh. 4.7 - Prob. 62ECh. 4.7 - A retailer has been selling 1200 tablet computers...Ch. 4.7 - Prob. 64ECh. 4.7 - Prob. 65ECh. 4.7 - Prob. 66ECh. 4.7 - Prob. 67ECh. 4.7 - Prob. 68ECh. 4.7 - A point P needs to be located somewhere on the...Ch. 4.7 - The graph shows the fuel consumption c of a car...Ch. 4.7 - Prob. 71ECh. 4.7 - Prob. 72ECh. 4.7 - Prob. 73ECh. 4.7 - Prob. 74ECh. 4.7 - Prob. 75ECh. 4.7 - Prob. 76ECh. 4.7 - Where should the point P be chosen on the line...Ch. 4.7 - Prob. 78ECh. 4.7 - Find the maximum area of a rectangle that can be...Ch. 4.7 - The blood vascular system consists of blood...Ch. 4.7 - Ornithologists have determined that some species...Ch. 4.7 - Prob. 82ECh. 4.8 - The figure shows the graph of a function f....Ch. 4.8 - Prob. 2ECh. 4.8 - Prob. 3ECh. 4.8 - For each initial approximation, determine...Ch. 4.8 - Prob. 5ECh. 4.8 - Prob. 6ECh. 4.8 - Prob. 7ECh. 4.8 - Prob. 8ECh. 4.8 - Prob. 9ECh. 4.8 - Prob. 10ECh. 4.8 - Prob. 11ECh. 4.8 - Prob. 12ECh. 4.8 - Prob. 13ECh. 4.8 - Prob. 14ECh. 4.8 - Prob. 15ECh. 4.8 - Prob. 16ECh. 4.8 - Prob. 17ECh. 4.8 - Prob. 18ECh. 4.8 - Prob. 19ECh. 4.8 - Prob. 20ECh. 4.8 - Prob. 21ECh. 4.8 - Prob. 22ECh. 4.8 - Prob. 23ECh. 4.8 - Prob. 24ECh. 4.8 - Prob. 25ECh. 4.8 - Prob. 26ECh. 4.8 - Prob. 27ECh. 4.8 - (a) Apply Newtons method to the equation x2 a = 0...Ch. 4.8 - Prob. 30ECh. 4.8 - Prob. 32ECh. 4.8 - Prob. 33ECh. 4.8 - If f(x)={xifx0xifx0 then the root of the equation...Ch. 4.8 - Prob. 35ECh. 4.8 - Prob. 36ECh. 4.8 - Prob. 37ECh. 4.8 - Use Newtons method to find the coordinates,...Ch. 4.8 - Prob. 40ECh. 4.8 - Prob. 41ECh. 4.8 - Prob. 42ECh. 4.9 - Find the most general antiderivative of the...Ch. 4.9 - Prob. 2ECh. 4.9 - Prob. 3ECh. 4.9 - Prob. 4ECh. 4.9 - Prob. 5ECh. 4.9 - Prob. 6ECh. 4.9 - Prob. 7ECh. 4.9 - Prob. 8ECh. 4.9 - Prob. 9ECh. 4.9 - Prob. 10ECh. 4.9 - Prob. 11ECh. 4.9 - Prob. 12ECh. 4.9 - Prob. 13ECh. 4.9 - Prob. 14ECh. 4.9 - Prob. 15ECh. 4.9 - Find the most general antiderivative of the...Ch. 4.9 - Prob. 17ECh. 4.9 - Prob. 18ECh. 4.9 - Find the most general antiderivative of the...Ch. 4.9 - Prob. 20ECh. 4.9 - Prob. 21ECh. 4.9 - Prob. 22ECh. 4.9 - Prob. 25ECh. 4.9 - Prob. 26ECh. 4.9 - Prob. 27ECh. 4.9 - Prob. 28ECh. 4.9 - Prob. 29ECh. 4.9 - Prob. 30ECh. 4.9 - Find f. f(x)=1+3x, f(4) = 25Ch. 4.9 - Prob. 32ECh. 4.9 - Prob. 33ECh. 4.9 - Find f. f(t) = t + 1/t3, t 0, f(1) = 6Ch. 4.9 - Prob. 35ECh. 4.9 - Prob. 36ECh. 4.9 - Prob. 37ECh. 4.9 - Prob. 38ECh. 4.9 - Prob. 39ECh. 4.9 - Prob. 40ECh. 4.9 - Prob. 41ECh. 4.9 - Prob. 42ECh. 4.9 - Prob. 43ECh. 4.9 - Find f. f(x) = x3 + sinh x, f(0) = 1, f(2) = 2.6Ch. 4.9 - Prob. 45ECh. 4.9 - Prob. 46ECh. 4.9 - Prob. 47ECh. 4.9 - Prob. 48ECh. 4.9 - Prob. 49ECh. 4.9 - Prob. 50ECh. 4.9 - Prob. 51ECh. 4.9 - The graph of a function f is shown. Which graph is...Ch. 4.9 - Prob. 53ECh. 4.9 - The graph of the velocity function of a particle...Ch. 4.9 - Prob. 55ECh. 4.9 - Prob. 56ECh. 4.9 - Prob. 57ECh. 4.9 - Prob. 58ECh. 4.9 - Prob. 59ECh. 4.9 - Prob. 60ECh. 4.9 - Prob. 61ECh. 4.9 - Prob. 62ECh. 4.9 - Prob. 63ECh. 4.9 - Prob. 64ECh. 4.9 - Prob. 65ECh. 4.9 - Prob. 66ECh. 4.9 - Prob. 67ECh. 4.9 - Two balls are thrown upward from the edge of the...Ch. 4.9 - Prob. 69ECh. 4.9 - If a diver of mass m stands at the end of a diving...Ch. 4.9 - Prob. 71ECh. 4.9 - Prob. 72ECh. 4.9 - Prob. 73ECh. 4.9 - Prob. 74ECh. 4.9 - Prob. 75ECh. 4.9 - Prob. 76ECh. 4.9 - A car is traveling at 100 km/h when the driver...Ch. 4.9 - A high-speed bullet train accelerates and...Ch. 4 - Explain the difference between an absolute maximum...Ch. 4 - Prob. 2RCCCh. 4 - Prob. 3RCCCh. 4 - Prob. 4RCCCh. 4 - Prob. 5RCCCh. 4 - Prob. 6RCCCh. 4 - Prob. 7RCCCh. 4 - Prob. 8RCCCh. 4 - Prob. 9RCCCh. 4 - Prob. 10RCCCh. 4 - Prob. 11RCCCh. 4 - Prob. 1RQCh. 4 - Prob. 2RQCh. 4 - If f is continuous on (a, b), then f attains an...Ch. 4 - Prob. 4RQCh. 4 - Prob. 5RQCh. 4 - If f(2) = 0, then (2, f(2)) is an inflection point...Ch. 4 - Prob. 7RQCh. 4 - Prob. 8RQCh. 4 - Prob. 9RQCh. 4 - Prob. 10RQCh. 4 - Prob. 11RQCh. 4 - Prob. 12RQCh. 4 - Prob. 13RQCh. 4 - If f and g are positive increasing functions on an...Ch. 4 - Prob. 15RQCh. 4 - Prob. 16RQCh. 4 - Prob. 17RQCh. 4 - Prob. 18RQCh. 4 - If f(x) exists and is nonzero for all x, then f(1)...Ch. 4 - Prob. 20RQCh. 4 - Prob. 21RQCh. 4 - Prob. 1RECh. 4 - Prob. 2RECh. 4 - Prob. 3RECh. 4 - Prob. 4RECh. 4 - Prob. 5RECh. 4 - Prob. 6RECh. 4 - Evaluate the limit. limx0ex1tanxCh. 4 - Prob. 8RECh. 4 - Prob. 9RECh. 4 - Prob. 10RECh. 4 - Prob. 11RECh. 4 - Prob. 12RECh. 4 - Prob. 13RECh. 4 - Prob. 14RECh. 4 - Prob. 15RECh. 4 - Prob. 16RECh. 4 - Prob. 17RECh. 4 - Prob. 18RECh. 4 - Prob. 19RECh. 4 - Prob. 20RECh. 4 - Prob. 21RECh. 4 - Prob. 22RECh. 4 - Prob. 23RECh. 4 - Prob. 24RECh. 4 - Prob. 25RECh. 4 - Prob. 26RECh. 4 - Prob. 27RECh. 4 - Prob. 28RECh. 4 - Prob. 29RECh. 4 - Prob. 30RECh. 4 - Prob. 31RECh. 4 - Prob. 32RECh. 4 - Prob. 33RECh. 4 - Prob. 34RECh. 4 - Prob. 35RECh. 4 - Prob. 36RECh. 4 - Prob. 37RECh. 4 - Prob. 38RECh. 4 - Prob. 39RECh. 4 - Prob. 43RECh. 4 - Prob. 44RECh. 4 - Prob. 45RECh. 4 - Prob. 46RECh. 4 - By applying the Mean Value Theorem to the function...Ch. 4 - Prob. 48RECh. 4 - Prob. 49RECh. 4 - Prob. 50RECh. 4 - Prob. 51RECh. 4 - Prob. 52RECh. 4 - Prob. 53RECh. 4 - Prob. 54RECh. 4 - Prob. 55RECh. 4 - Prob. 56RECh. 4 - Prob. 57RECh. 4 - Prob. 58RECh. 4 - A hockey team plays in an arena with a seating...Ch. 4 - Prob. 60RECh. 4 - Prob. 61RECh. 4 - Prob. 62RECh. 4 - Prob. 63RECh. 4 - Prob. 64RECh. 4 - Prob. 65RECh. 4 - Prob. 66RECh. 4 - Prob. 67RECh. 4 - Prob. 68RECh. 4 - Prob. 69RECh. 4 - Prob. 70RECh. 4 - Prob. 71RECh. 4 - Prob. 72RECh. 4 - Prob. 73RECh. 4 - Prob. 74RECh. 4 - Prob. 75RECh. 4 - Prob. 76RECh. 4 - Prob. 77RECh. 4 - Prob. 78RECh. 4 - Prob. 79RECh. 4 - If a projectile is fired with an initial velocity...Ch. 4 - Prob. 81RECh. 4 - If a metal ball with mass m is projected in water...Ch. 4 - Prob. 83RECh. 4 - Prob. 84RECh. 4 - Prob. 85RECh. 4 - Prob. 86RECh. 4 - Prob. 1PCh. 4 - Prob. 2PCh. 4 - Prob. 3PCh. 4 - Prob. 4PCh. 4 - Prob. 5PCh. 4 - Prob. 6PCh. 4 - If a, b, c, and d are constants such that...Ch. 4 - Prob. 8PCh. 4 - Prob. 9PCh. 4 - Prob. 10PCh. 4 - Prob. 11PCh. 4 - For what values of c does the curve y = cx3 + ex...Ch. 4 - Prob. 13PCh. 4 - Prob. 14PCh. 4 - Prob. 15PCh. 4 - Prob. 16PCh. 4 - Prob. 17PCh. 4 - Prob. 18PCh. 4 - Prob. 19PCh. 4 - An arc PQ of a circle subtends a central angle as...Ch. 4 - Prob. 21PCh. 4 - Prob. 22PCh. 4 - Prob. 23PCh. 4 - Prob. 25PCh. 4 - A hemispherical bubble is placed on a spherical...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- Let N be any point on side BC of the right triangle ABC. Find the upper and lower limits for the length of AN.arrow_forwardWhat is the limit of mRTS if T lies in the interior of the shaded region?arrow_forwardSuppose that the circle with center 0, 0 and radius length r contains the point a,b. Find the slope of the tangent line to the circle at the point a,b.arrow_forward
- Find the length of the arc of y=x^(3/2) between the points (1,1) and (4,8).arrow_forwardthe circle is the tangent to both x and y axis. A point on the circle is (2,1). Calculate the area of the circlearrow_forwardFrom the vertex (0, c) of the catenary y = c cosh(x/c) a line L is drawn perpendicular to the tangent to the catenary at point P. Prove that the length of L intercepted by the axes is equal to the ordinate y of the point P.arrow_forward
- Tangents are drawn to the concentric circles x^(2)+y^(2)=a^(2) and x^(2)+y^(2)=b^(2) at right angle to one another. Show/Prove that the locus of their point of intersection is a 3rd concentric circle. Find its radius.arrow_forwardThe curve y = sqrt ( 4 - x sq. ) ,-1 < = x < = 1 , is an arc of the circle x sq. + y sq. = 4 . Find the area of the surface obtained by rotating this arc about thex -axis.arrow_forwardShow that the area of the region in the first quadrant en-closed by the curve y = (1/a) cosh ax, the coordinate axes, and the line x = b is the same as the area of a rectangle of height 1 /a and length s, where s is the length of the curve from x = 0 to x = b. Draw a figure illustrating this result.arrow_forward
- Find the arc length of the graph by partitioning the x-axis. y=(1-x2/3)3/2 , from x= 1/64 to x=1arrow_forwardLet R be the area of the region in the first quadrant bounded by the parabola y = x2 and the line y = cx, c > 0, as shown in the figure. Let T be the area of the triangle AOB. Calculate the limitarrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage Trigonometry (MindTap Course List)TrigonometryISBN:9781305652224Author:Charles P. McKeague, Mark D. TurnerPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781305652224Author:Charles P. McKeague, Mark D. TurnerPublisher:Cengage Learning Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning

Elementary Geometry For College Students, 7e
Geometry
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Cengage,

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage

Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781305652224
Author:Charles P. McKeague, Mark D. Turner
Publisher:Cengage Learning

Algebra and Trigonometry (MindTap Course List)
Algebra
ISBN:9781305071742
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:Cengage Learning
Differential Equation | MIT 18.01SC Single Variable Calculus, Fall 2010; Author: MIT OpenCourseWare;https://www.youtube.com/watch?v=HaOHUfymsuk;License: Standard YouTube License, CC-BY