Chapter 4, Problem 48RE

(a)

To determine

To find: The production level for maximum profit by the graphs.

Answer to Problem 48RE

The production level of $x=160$ units will be maximum profit

Explanation of Solution

Given information:

The given information is

Commodity is $C\left(x\right)=1800+25x-0.2x^2+0.001x^3$

Demand function is $p\left(x\right)=48.2-0.03x$ .

Calculation:

The cost function is $C\left(x\right)=1800+25x-0.2x^2+0.001x^3$

Demand function is $p\left(x\right)=48.2-0.03x$

The revenue function $R\left(x\right)=x.p\left(x\right)$

Or $R\left(x\right)=48.2x-0.03x^2$

Now we draw the curve of $C\left(x\right)$ and $R\left(x\right)$ on the same screen and get that Manufacturers has profit when $R>C$ , and maximum profit occurs when R and C have parallel tangents.

That is at the production level of $x=160$ units.

  

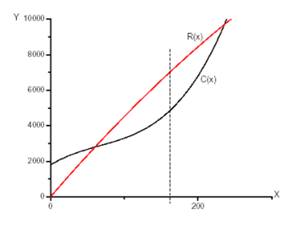
Therefore, the production level of $x=160$ units will be maximum profit.

(b)

To determine

To find: The production level for maximum profit by calculus method.

Answer to Problem 48RE

The production level $161$ units will maximize the profit.

Explanation of Solution

Given information:

The given information is

Commodity is $C\left(x\right)=1800+25x-0.2x^2+0.001x^3$

Demand function is $p\left(x\right)=48.2-0.03x$ .

Calculation:

Now the marginal revenue function is

  $R^{\text{'}}\left(x\right)=48.2-0.06x$

And marginal cost function is

  $C\text{'}\left(x\right)=25x-0.4x+0.003x^3$

For maximize the profit we must have

  $R\text{'}\left(x\right)=C\text{'}\left(x\right)$

Or $\begin{array}{l}48.2-0.06x=25x-0.4x+0.003x^3\\ 0.003x^2-0.34x-23.2=0\end{array}$

The root of the equation $a{x}^2+bx+c=0$

  $x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}$

Here we are not considering $x=\frac{-b-\sqrt{b^2-4ac}}{2a}$ because $x>0$ .

Thus we have

  $x=\frac{0.34+\sqrt{{\left(-0.34\right)}^2-4\times 0.003\times 23.2}}{0.006}$

  $x=161$ Units.

Since $R\text{'}\left(x\right)=-0.06$ and $C\text{'}\left(x\right)=0.006x-0.4$

So $R\text{'}\left(x\right)<C\left(x\right)$ for $x=161$ units

Therefore, the production level $161$ units will maximize the profit.

(c)

To determine

To find: The production level that minimizes the average cost.

Answer to Problem 48RE

The production level of $144$ units the average cost is minimum

Explanation of Solution

Given information:

The given information is

Commodity is $C\left(x\right)=1800+25x-0.2x^2+0.001x^3$

Demand function is $p\left(x\right)=48.2-0.03x$ .

Calculation:

Now the average cost function is

  $c\left(x\right)=\frac{C\left(x\right)}{x}=\frac{1800}{x}+25-0.2x+0.001x^2$

And marginal cost is

  $C\text{'}\left(x\right)=25x-0.4x+0.003x^3$

For minimum average cost we must have

  $c\left(x\right)=C\text{'}\left(x\right)$

  $\begin{array}{l}\frac{1800}{x}+25-0.2x+0.001x^2=25x-0.4x+0.003x^3\\ 0.002x^3-0.2x^2=1800\end{array}$

By graphical method

We draw the curve $f\left(x\right)=0.002x^3-0.2x^2$ and $y=1800$ .

  

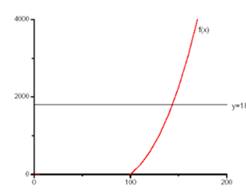
We estimate the point of intersection of these curves. The x-coordinate of the point of intersection is about $144$ units.

So at the production level of $144$ units the average cost is minimum.

Now,

  $c\left(x\right)=\frac{C\left(x\right)}{x}=\frac{1800}{x}+25-0.2x+0.001x^2$

Then $c\text{'}\left(x\right)=\frac{1800}{x^2}-0.2+0.002x$

And $c\text{'}\text{'}\left(x\right)=2\times \frac{1800}{x^3}+0.002>0$ for all $x>0$

So at $x=144,c\left(x\right)$ has an absolute minimum.