
Concept explainers
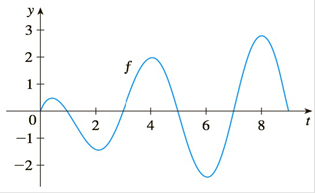
Let
graph is shown.
(a) At what values of x do the
(b) Where does g attain its absolute maximum value?
(c) On what intervals is g concave downward?
(d) Sketch the graph of g.
Trending nowThis is a popular solution!

Chapter 4 Solutions
Calculus (MindTap Course List)
Additional Math Textbook Solutions
Precalculus: A Unit Circle Approach
Calculus: Early Transcendentals (3rd Edition)
University Calculus: Early Transcendentals, Single Variable (3rd Edition)
Finite Mathematics and Calculus with Applications (10th Edition)
Glencoe Math Accelerated, Student Edition
Thomas' Calculus: Early Transcendentals (14th Edition)
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
 College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning College AlgebraAlgebraISBN:9781305115545Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
College AlgebraAlgebraISBN:9781305115545Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning 



