Chapter 4.7, Problem 27E

Explain why Newton’s method fails when applied to the equation $\sqrt[3]{x}=0$ with any initial approximation x₁ ≠ 0. Illustrate your explanation with a sketch.

To determine

To find: The Newton’s method fails for the given equation with any approximation $x_1\ne 0$ with sketch the graph.

Explanation of Solution

Given:

The equation is $x^{\frac{1}{3}}=0$.

The initial approximation is $x_1=0.5$.

Result Used:

The Newton’s method is $x_{n+1}=x_n-\frac{f\left(x_n\right)}{f^{\prime }\left(x_n\right)}$.

Graph:

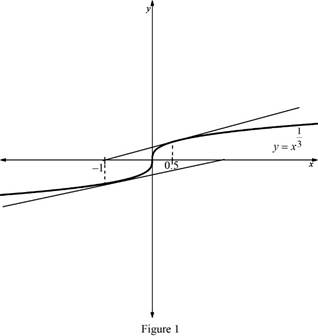
From the Figure 1, it is observed that the value gets doubled.

Calculation:

Let $f\left(x\right)=x^{\frac{1}{3}}$, then $f\left(x\right)=0$ by the given condition.

Calculate the derivative of $f\left(x\right)$.

Let $f^{\prime }\left(x\right)=\frac{df\left(x\right)}{dx}$.

$\begin{array}{c}{f}^{\prime }\left(x\right)=\frac{d\left(x^{\frac{1}{3}}\right)}{dx}\\ =\frac{1}{3}{x}^{-\frac{2}{3}}\end{array}$

Substitute the value of $f\left(x\right)$ and $f^{\prime }\left(x\right)$ in the above mentioned result to obtain $x_{n+1}$.

$\begin{array}{c}{x}_{n+1}=x_n-\frac{x_n^{\frac{1}{3}}}{\frac{1}{3}{x}_n^{-\frac{2}{3}}}\\ =x_n-3x_n\\ =-2x_n\end{array}$

Set $n=1$, $x_1=0.5$ and obtain $x_2$ from the above expression.

$\begin{array}{c}{x}_2=-2\times 0.5\\ =-1\end{array}$

Set $n=2$, $x_2=-1$ and obtain $x_3$ from the above expression.

$\begin{array}{c}{x}_3=-2\times \left(-1\right)\\ =2\end{array}$

Similarly, proceed in the above manner.

Observation:

From the above calculation, each successive approximation gives the value twice than previous value.

Thus, if we consider the sequence of the Newton’s approximation fails to converge to the root $0$. Therefore, the Newton’s method fails.