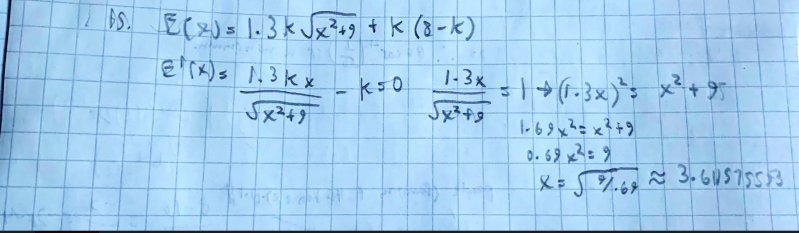
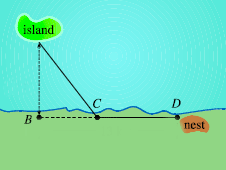
Ornithologists have determined that some species of birds tend to avoid flights over large bodies of water during daylight hours. It is believed that more energy is required to fly over water than land because air generally rises over land and falls over water during the day. A bird with these tendencies is released from an island that is 3 km from the nearest point B on the shoreline, flies to a point C on the shoreline, and then flies along the shoreline to its nesting area D. Assume that the bird instinctively chooses a path that will minimize its energy expenditure. Points B and D are 8 km apart. (Round your answers to two decimal places.) In general, if it takes 1.3 times as much energy to fly over water as land, to what point C should the bird fly in order to minimize the total energy expended in returning to its nesting area?
Ornithologists have determined that some species of birds tend to avoid flights over large bodies of water during daylight hours. It is believed that more energy is required to fly over water than land because air generally rises over land and falls over water during the day. A bird with these tendencies is released from an island that is 3 km from the nearest point B on the shoreline, flies to a point C on the shoreline, and then flies along the shoreline to its nesting area D. Assume that the bird instinctively chooses a path that will minimize its energy expenditure. Points B and D are 8 km apart. (Round your answers to two decimal places.)
In general, if it takes 1.3 times as much energy to fly over water as land, to what point C should the bird fly in order to minimize the total energy expended in returning to its nesting area?
Trending now
This is a popular solution!
Step by step
Solved in 6 steps with 2 images




