
Calculus: An Applied Approach (MindTap Course List)
10th Edition
ISBN: 9781305860919
Author: Ron Larson
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Concept explainers
Textbook Question
Chapter 5, Problem 104RE
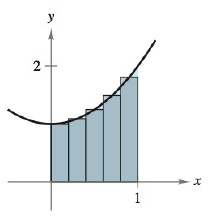
Approximating the Area of a Plane Region In Exercises 103 and 104, use the rectangles to approximate the area of the region. Compare your result with the exact area obtained using a definite
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Using Completing the square evaluate the integral below
Integral Calculus
Finding Area under the Curve
1. Determine the area to the left og g(y)=3-y^2 and to the right of x=-1
Integral Calculus
Find the area bounded by the curves y=x^3-18x and x+2y=0
Chapter 5 Solutions
Calculus: An Applied Approach (MindTap Course List)
Ch. 5.1 - Checkpoint 1 Worked-out solution available at...Ch. 5.1 - Prob. 2CPCh. 5.1 - Prob. 3CPCh. 5.1 - Prob. 4CPCh. 5.1 - Prob. 5CPCh. 5.1 - Prob. 6CPCh. 5.1 - Checkpoint 7 Worked-out solution available at...Ch. 5.1 - Prob. 8CPCh. 5.1 - Prob. 1SWUCh. 5.1 - Prob. 2SWU
Ch. 5.1 - Prob. 3SWUCh. 5.1 - Prob. 4SWUCh. 5.1 - Prob. 5SWUCh. 5.1 - Prob. 6SWUCh. 5.1 - In Exercises 7-10, let (x, y) = (2, 2), and solve...Ch. 5.1 - Prob. 8SWUCh. 5.1 - Prob. 9SWUCh. 5.1 - Prob. 10SWUCh. 5.1 - Integration and Differentiation In Exercises 1- 6,...Ch. 5.1 - Integration and Differentiation In Exercises 1- 6,...Ch. 5.1 - Integration and Differentiation In Exercises 1- 6,...Ch. 5.1 - Integration and Differentiation In Exercises 1- 6,...Ch. 5.1 - Integration and Differentiation In Exercises 1- 6,...Ch. 5.1 - Prob. 6ECh. 5.1 - Finding Indefinite Integrals In Exercises 7-18,...Ch. 5.1 - Prob. 8ECh. 5.1 - Finding Indefinite Integrals In Exercises 7-18,...Ch. 5.1 - Prob. 10ECh. 5.1 - Prob. 11ECh. 5.1 - Prob. 12ECh. 5.1 - Finding Indefinite Integrals In Exercises 7-18,...Ch. 5.1 - Prob. 14ECh. 5.1 - Finding Indefinite Integrals In Exercises 7-18,...Ch. 5.1 - Finding Indefinite Integrals In Exercises 7-18,...Ch. 5.1 - Finding Indefinite Integrals In Exercises 7-18,...Ch. 5.1 - Prob. 18ECh. 5.1 - Rewriting Before Integrating In Exercises 19-24,...Ch. 5.1 - Prob. 20ECh. 5.1 - Rewriting Before Integrating In Exercises 19-24,...Ch. 5.1 - Rewriting Before Integrating In Exercises 19-24,...Ch. 5.1 - Rewriting Before Integrating In Exercises 19-24,...Ch. 5.1 - Prob. 24ECh. 5.1 - Finding Indefinite Integrals In Exercises 25-36,...Ch. 5.1 - Prob. 26ECh. 5.1 - Finding indefinite integrals In Exercises 2536,...Ch. 5.1 - Prob. 28ECh. 5.1 - Finding indefinite integrals In Exercises 2536,...Ch. 5.1 - Prob. 30ECh. 5.1 - Finding indefinite integrals In Exercises 2536,...Ch. 5.1 - Prob. 32ECh. 5.1 - Finding indefinite integrals In Exercises 2536,...Ch. 5.1 - Prob. 34ECh. 5.1 - Finding indefinite integrals In Exercises 2536,...Ch. 5.1 - Prob. 36ECh. 5.1 - Using Technology In Exercises 37 and 38, use a...Ch. 5.1 - Prob. 38ECh. 5.1 - Prob. 39ECh. 5.1 - Prob. 40ECh. 5.1 - Interpreting a Graph In Exercises 3942, the graph...Ch. 5.1 - Prob. 42ECh. 5.1 - Finding a Particular Solution In Exercises 4350,...Ch. 5.1 - Prob. 44ECh. 5.1 - Finding a Particular Solution In Exercises 4350,...Ch. 5.1 - Finding a Particular Solution In Exercises 4350,...Ch. 5.1 - Prob. 47ECh. 5.1 - Prob. 48ECh. 5.1 - Finding a Particular Solution In Exercises 4350,...Ch. 5.1 - Prob. 50ECh. 5.1 - Prob. 51ECh. 5.1 - Prob. 52ECh. 5.1 - Prob. 53ECh. 5.1 - Prob. 54ECh. 5.1 - Finding a Cost Function In Exercises 5558, find...Ch. 5.1 - Prob. 56ECh. 5.1 - Finding a Cost Function In Exercises 5558, find...Ch. 5.1 - Prob. 58ECh. 5.1 - Revenue and Demand In Exercises 59 and 60, find...Ch. 5.1 - Prob. 60ECh. 5.1 - Prob. 61ECh. 5.1 - Prob. 62ECh. 5.1 - Prob. 63ECh. 5.1 - Prob. 64ECh. 5.1 - Vertical Motion In Exercises 6568, use s(t)=32...Ch. 5.1 - Prob. 66ECh. 5.1 - Prob. 67ECh. 5.1 - Prob. 68ECh. 5.1 - Prob. 69ECh. 5.1 - Gardening An evergreen nursery usually sells a...Ch. 5.1 - Population growth The growth rate of the...Ch. 5.1 - Prob. 72ECh. 5.1 - Vital Statistics The rate of increase of the...Ch. 5.1 - Prob. 74ECh. 5.1 - Economics: Marginal Benefits and Costs The table...Ch. 5.2 - Checkpoint 1 Worked-out solution available at...Ch. 5.2 - Prob. 2CPCh. 5.2 - Prob. 3CPCh. 5.2 - Prob. 4CPCh. 5.2 - Prob. 5CPCh. 5.2 - Prob. 6CPCh. 5.2 - Checkpoint 7 Worked-out solution available at...Ch. 5.2 - Prob. 8CPCh. 5.2 - Prob. 1SWUCh. 5.2 - Prob. 2SWUCh. 5.2 - Prob. 3SWUCh. 5.2 - Prob. 4SWUCh. 5.2 - Prob. 5SWUCh. 5.2 - Prob. 6SWUCh. 5.2 - Prob. 7SWUCh. 5.2 - Prob. 8SWUCh. 5.2 - Prob. 9SWUCh. 5.2 - Finding u and du/dx In Exercises 1-8, identify u...Ch. 5.2 - Finding u and du/dx In Exercises 1-8, identify u...Ch. 5.2 - Finding u and du/dx In Exercises 1-8, identify u...Ch. 5.2 - Prob. 4ECh. 5.2 - Prob. 5ECh. 5.2 - Prob. 6ECh. 5.2 - Finding u and du/dx In Exercises 1-8, identify u...Ch. 5.2 - Prob. 8ECh. 5.2 - Applying the General Power Rule In Exercises 9-34,...Ch. 5.2 - Prob. 10ECh. 5.2 - Prob. 11ECh. 5.2 - Prob. 12ECh. 5.2 - Applying the General Power Rule In Exercises 9-34,...Ch. 5.2 - Prob. 14ECh. 5.2 - Applying the General Power Rule In Exercises 9-34,...Ch. 5.2 - Prob. 16ECh. 5.2 - Prob. 17ECh. 5.2 - Prob. 18ECh. 5.2 - Applying the General Power Rule In Exercises 9-34,...Ch. 5.2 - Applying the General Power Rule In Exercises 9-34,...Ch. 5.2 - Applying the General Power Rule In Exercises 9-34,...Ch. 5.2 - Prob. 22ECh. 5.2 - Applying the General Power Rule In Exercises 9-34,...Ch. 5.2 - Applying the General Power Rule In Exercises 9-34,...Ch. 5.2 - Applying the General Power Rule In Exercises 934,...Ch. 5.2 - Prob. 26ECh. 5.2 - Applying the General Power Rule In Exercises 934,...Ch. 5.2 - Prob. 28ECh. 5.2 - Prob. 29ECh. 5.2 - Prob. 30ECh. 5.2 - Prob. 31ECh. 5.2 - Prob. 32ECh. 5.2 - Applying the General Power Rule In Exercises 934,...Ch. 5.2 - Prob. 34ECh. 5.2 - Prob. 35ECh. 5.2 - Prob. 36ECh. 5.2 - Prob. 37ECh. 5.2 - Prob. 38ECh. 5.2 - Prob. 39ECh. 5.2 - Prob. 40ECh. 5.2 - Integration by Substitution In Exercises 3542, use...Ch. 5.2 - Prob. 42ECh. 5.2 - Comparing Methods In Exercises 43-46, (a) perform...Ch. 5.2 - Prob. 44ECh. 5.2 - Prob. 45ECh. 5.2 - Comparing Methods In Exercises 43-46, (a) perform...Ch. 5.2 - Prob. 47ECh. 5.2 - Prob. 48ECh. 5.2 - Prob. 49ECh. 5.2 - Prob. 50ECh. 5.2 - Prob. 51ECh. 5.2 - Prob. 52ECh. 5.2 - Prob. 53ECh. 5.2 - Prob. 54ECh. 5.2 - Supply In Exercises 53 and 54, find the supply...Ch. 5.2 - Supply In Exercises 53 and 54, find the supply...Ch. 5.2 - Gardening An evergreen nursery usually sells a...Ch. 5.2 - HOW DO YOU SEE IT? The graph shows the rate of...Ch. 5.2 - Prob. 59ECh. 5.2 - Marginal Propensity to Consume In Exercises 59 and...Ch. 5.2 - Prob. 61ECh. 5.2 - Prob. 62ECh. 5.3 - Checkpoint 1 Worked-out solution available at...Ch. 5.3 - Checkpoint 2 Worked out solution available at...Ch. 5.3 - Prob. 3CPCh. 5.3 - Checkpoint 4 Worked-out solution available at...Ch. 5.3 - Prob. 5CPCh. 5.3 - Prob. 6CPCh. 5.3 - Prob. 7CPCh. 5.3 - Prob. 1SWUCh. 5.3 - Prob. 2SWUCh. 5.3 - Prob. 3SWUCh. 5.3 - Prob. 4SWUCh. 5.3 - Prob. 5SWUCh. 5.3 - Prob. 6SWUCh. 5.3 - Prob. 7SWUCh. 5.3 - Prob. 8SWUCh. 5.3 - Integrating an Exponential Function In Exercises...Ch. 5.3 - Prob. 2ECh. 5.3 - Integrating an Exponential Function In Exercises...Ch. 5.3 - Prob. 4ECh. 5.3 - Prob. 5ECh. 5.3 - Prob. 6ECh. 5.3 - Integrating an Exponential Function In Exercises...Ch. 5.3 - Prob. 8ECh. 5.3 - Integrating an Exponential Function In Exercises...Ch. 5.3 - Prob. 10ECh. 5.3 - Prob. 11ECh. 5.3 - Prob. 12ECh. 5.3 - Using the log Rule for integration In Exercises...Ch. 5.3 - Prob. 14ECh. 5.3 - Using the log Rule for integration In Exercises...Ch. 5.3 - Prob. 16ECh. 5.3 - Prob. 17ECh. 5.3 - Prob. 18ECh. 5.3 - Using the log Rule for integration In Exercises...Ch. 5.3 - Prob. 20ECh. 5.3 - Using the log Rule for integration In Exercises...Ch. 5.3 - Prob. 22ECh. 5.3 - Using the log Rule for integration In Exercises...Ch. 5.3 - Prob. 24ECh. 5.3 - Using the log Rule for integration In Exercises...Ch. 5.3 - Prob. 26ECh. 5.3 - Using the log Rule for integration In Exercises...Ch. 5.3 - Using the log Rule for integration In Exercises...Ch. 5.3 - Prob. 29ECh. 5.3 - Prob. 30ECh. 5.3 - Prob. 31ECh. 5.3 - Finding indefinite integrals In Exercises 3146,...Ch. 5.3 - Finding indefinite integrals In Exercises 3146,...Ch. 5.3 - Prob. 34ECh. 5.3 - Finding indefinite integrals In Exercises 3146,...Ch. 5.3 - Prob. 36ECh. 5.3 - Prob. 37ECh. 5.3 - Prob. 38ECh. 5.3 - Finding indefinite integrals In Exercises 3146,...Ch. 5.3 - Finding indefinite integrals In Exercises 3146,...Ch. 5.3 - Prob. 41ECh. 5.3 - Prob. 42ECh. 5.3 - Finding indefinite integrals In Exercises 3146,...Ch. 5.3 - Finding indefinite integrals In Exercises 3146,...Ch. 5.3 - Prob. 45ECh. 5.3 - Prob. 46ECh. 5.3 - Prob. 47ECh. 5.3 - Prob. 48ECh. 5.3 - Prob. 49ECh. 5.3 - Prob. 50ECh. 5.3 - Prob. 51ECh. 5.3 - Biology Because of an insufficient oxygen supply,...Ch. 5.3 - Demand The marginal price for the demand of a...Ch. 5.3 - Prob. 54ECh. 5.3 - Revenue The rate of change in revenue for the...Ch. 5.3 - Revenue The rate of change in revenue for DIRECTV...Ch. 5.3 - True or False In Exercises 57 and 58, determine...Ch. 5.3 - Prob. 58ECh. 5.3 - Prob. 1QYCh. 5.3 - Prob. 2QYCh. 5.3 - Prob. 3QYCh. 5.3 - Prob. 4QYCh. 5.3 - Prob. 5QYCh. 5.3 - Prob. 6QYCh. 5.3 - Prob. 7QYCh. 5.3 - Prob. 8QYCh. 5.3 - Prob. 9QYCh. 5.3 - Prob. 10QYCh. 5.3 - Prob. 11QYCh. 5.3 - Prob. 12QYCh. 5.3 - Prob. 13QYCh. 5.3 - Prob. 14QYCh. 5.3 - Prob. 15QYCh. 5.3 - Prob. 16QYCh. 5.3 - Prob. 17QYCh. 5.3 - Prob. 18QYCh. 5.3 - Prob. 19QYCh. 5.3 - Prob. 20QYCh. 5.3 - Prob. 21QYCh. 5.4 - Checkpoint 1 Worked-out solution available at...Ch. 5.4 - Prob. 2CPCh. 5.4 - Prob. 3CPCh. 5.4 - Prob. 4CPCh. 5.4 - Prob. 5CPCh. 5.4 - Prob. 6CPCh. 5.4 - Prob. 7CPCh. 5.4 - Prob. 8CPCh. 5.4 - Prob. 9CPCh. 5.4 - Prob. 1SWUCh. 5.4 - Prob. 2SWUCh. 5.4 - Prob. 3SWUCh. 5.4 - Prob. 4SWUCh. 5.4 - Prob. 5SWUCh. 5.4 - Prob. 6SWUCh. 5.4 - Prob. 7SWUCh. 5.4 - Evaluating a Definite integral using a Geometric...Ch. 5.4 - Prob. 2ECh. 5.4 - Evaluating a Definite integral using a Geometric...Ch. 5.4 - Prob. 4ECh. 5.4 - Evaluating a Definite integral using a Geometric...Ch. 5.4 - Prob. 6ECh. 5.4 - Using Properties of Definite Integrals In...Ch. 5.4 - Using Properties of Definite Integrals In...Ch. 5.4 - Finding Area by the Fundamental Theorem In...Ch. 5.4 - Finding Area by the Fundamental Theorem In...Ch. 5.4 - Finding Area by the Fundamental Theorem In...Ch. 5.4 - Prob. 12ECh. 5.4 - Finding Area by the Fundamental Theorem In...Ch. 5.4 - Prob. 14ECh. 5.4 - Finding Area by the Fundamental Theorem In...Ch. 5.4 - Prob. 16ECh. 5.4 - Evaluating a Definite Integral In Exercises 17-38,...Ch. 5.4 - Evaluating a Definite Integral In Exercises 17-38,...Ch. 5.4 - Evaluating a Definite Integral In Exercises 17-38,...Ch. 5.4 - Prob. 20ECh. 5.4 - Evaluating a Definite Integral In Exercises 17-38,...Ch. 5.4 - Prob. 22ECh. 5.4 - Prob. 23ECh. 5.4 - Prob. 24ECh. 5.4 - Evaluating a Definite Integral In Exercises 17-38,...Ch. 5.4 - Prob. 26ECh. 5.4 - Evaluating a Definite Integral In Exercises 17-38,...Ch. 5.4 - Prob. 28ECh. 5.4 - Evaluating a Definite Integral In Exercises 17-38,...Ch. 5.4 - Prob. 30ECh. 5.4 - Evaluating a Definite Integral In Exercises 17-38,...Ch. 5.4 - Evaluating a Definite Integral In Exercises 17-38,...Ch. 5.4 - Prob. 33ECh. 5.4 - Evaluating a Definite Integral In Exercises 17-38,...Ch. 5.4 - Evaluating a Definite Integral In Exercises 1738,...Ch. 5.4 - Evaluating a Definite Integral In Exercises 1738,...Ch. 5.4 - Prob. 37ECh. 5.4 - Prob. 38ECh. 5.4 - Definite Integral Involving Absolute Value In...Ch. 5.4 - Definite Integral Involving Absolute Value In...Ch. 5.4 - Definite Integral Involving Absolute Value In...Ch. 5.4 - Prob. 42ECh. 5.4 - Prob. 43ECh. 5.4 - Prob. 44ECh. 5.4 - Prob. 45ECh. 5.4 - Prob. 46ECh. 5.4 - Prob. 47ECh. 5.4 - Prob. 48ECh. 5.4 - Prob. 49ECh. 5.4 - Prob. 50ECh. 5.4 - Prob. 51ECh. 5.4 - Prob. 52ECh. 5.4 - Prob. 53ECh. 5.4 - Prob. 54ECh. 5.4 - Prob. 55ECh. 5.4 - Prob. 56ECh. 5.4 - Prob. 57ECh. 5.4 - Prob. 58ECh. 5.4 - Prob. 59ECh. 5.4 - Prob. 60ECh. 5.4 - Prob. 61ECh. 5.4 - Prob. 62ECh. 5.4 - Integrating Even and Odd Functions In Exercises...Ch. 5.4 - Prob. 64ECh. 5.4 - Using Properties of Definite Integrals Use the...Ch. 5.4 - Prob. 66ECh. 5.4 - Finding the Amount of an Annuity In Exercises...Ch. 5.4 - Prob. 68ECh. 5.4 - Finding the Amount of an Annuity In Exercises...Ch. 5.4 - Prob. 70ECh. 5.4 - Capital Accumulation In Exercises 71-74, you are...Ch. 5.4 - Prob. 72ECh. 5.4 - Prob. 73ECh. 5.4 - Capital Accumulation In Exercises 71-74, you are...Ch. 5.4 - Cost The total cost of purchasing a piece of...Ch. 5.4 - Depreciation A company purchases a new machine for...Ch. 5.4 - Prob. 77ECh. 5.4 - HOW DO YOU SEE IT? A college graduate has two job...Ch. 5.4 - Mortgage Debt The rate of change of mortgage debt...Ch. 5.5 - Checkpoint 1 Worked-out solution available at...Ch. 5.5 - Prob. 2CPCh. 5.5 - Prob. 3CPCh. 5.5 - Prob. 4CPCh. 5.5 - Prob. 5CPCh. 5.5 - Prob. 6CPCh. 5.5 - Prob. 1SWUCh. 5.5 - Prob. 2SWUCh. 5.5 - Prob. 3SWUCh. 5.5 - Prob. 4SWUCh. 5.5 - Prob. 5SWUCh. 5.5 - Prob. 6SWUCh. 5.5 - Prob. 7SWUCh. 5.5 - Prob. 8SWUCh. 5.5 - Finding the Area Bounded by Two Graphs In...Ch. 5.5 - Prob. 2ECh. 5.5 - Finding the Area Bounded by Two Graphs In...Ch. 5.5 - Prob. 4ECh. 5.5 - Finding the Area Bounded by Two Graphs In...Ch. 5.5 - Prob. 6ECh. 5.5 - Prob. 7ECh. 5.5 - Finding the Area Bounded by Two Graphs In...Ch. 5.5 - Prob. 9ECh. 5.5 - Prob. 10ECh. 5.5 - Prob. 11ECh. 5.5 - Prob. 12ECh. 5.5 - Prob. 13ECh. 5.5 - Prob. 14ECh. 5.5 - Finding the Area Bounded by Two Graphs In...Ch. 5.5 - Prob. 16ECh. 5.5 - Finding the Area Bounded by Two Graphs In...Ch. 5.5 - Prob. 18ECh. 5.5 - Prob. 19ECh. 5.5 - Prob. 20ECh. 5.5 - Prob. 21ECh. 5.5 - Prob. 22ECh. 5.5 - Finding the Area Bounded by Two Graphs In...Ch. 5.5 - Prob. 24ECh. 5.5 - Prob. 25ECh. 5.5 - Prob. 26ECh. 5.5 - Prob. 27ECh. 5.5 - Prob. 28ECh. 5.5 - Prob. 29ECh. 5.5 - Prob. 30ECh. 5.5 - Prob. 31ECh. 5.5 - Prob. 32ECh. 5.5 - Prob. 33ECh. 5.5 - Prob. 34ECh. 5.5 - Prob. 35ECh. 5.5 - Prob. 36ECh. 5.5 - Prob. 37ECh. 5.5 - Prob. 38ECh. 5.5 - Prob. 39ECh. 5.5 - Prob. 40ECh. 5.5 - Prob. 41ECh. 5.5 - Prob. 42ECh. 5.5 - Consumer and Producer Surpluses In Exercises...Ch. 5.5 - Consumer and Producer Surpluses In Exercises...Ch. 5.5 - Consumer and Producer Surpluses In Exercises...Ch. 5.5 - Consumer and Producer Surpluses In Exercises...Ch. 5.5 - Consumer and Producer Surpluses In Exercises...Ch. 5.5 - Prob. 48ECh. 5.5 - Revenue In Exercises 49 and 50, two models, R1 and...Ch. 5.5 - Revenue In Exercises 49 and 50, two models, R1 and...Ch. 5.5 - Fuel Cost The projected fuel cost C (in millions...Ch. 5.5 - Health An epidemic was spreading such that t weeks...Ch. 5.5 - Prob. 53ECh. 5.5 - HOW DO YOU SEE IT? A state legislature is debating...Ch. 5.5 - Prob. 55ECh. 5.5 - Prob. 56ECh. 5.5 - Consumer and Producer Surpluses Factory orders for...Ch. 5.5 - Consumer and Producer Surpluses Repeat Exercise 57...Ch. 5.6 - Prob. 1CPCh. 5.6 - Prob. 2CPCh. 5.6 - Prob. 3CPCh. 5.6 - Prob. 1SWUCh. 5.6 - Prob. 2SWUCh. 5.6 - Prob. 3SWUCh. 5.6 - Prob. 4SWUCh. 5.6 - Prob. 5SWUCh. 5.6 - Prob. 6SWUCh. 5.6 - Prob. 7SWUCh. 5.6 - Prob. 8SWUCh. 5.6 - Prob. 9SWUCh. 5.6 - Prob. 10SWUCh. 5.6 - Approximating the Area of a Plane Region In...Ch. 5.6 - Prob. 2ECh. 5.6 - Prob. 3ECh. 5.6 - Prob. 4ECh. 5.6 - Prob. 5ECh. 5.6 - Approximating the Area of a Plane Region In...Ch. 5.6 - Prob. 7ECh. 5.6 - Prob. 8ECh. 5.6 - Prob. 9ECh. 5.6 - Prob. 10ECh. 5.6 - Prob. 11ECh. 5.6 - Prob. 12ECh. 5.6 - Prob. 13ECh. 5.6 - Prob. 14ECh. 5.6 - Prob. 15ECh. 5.6 - Prob. 16ECh. 5.6 - Prob. 17ECh. 5.6 - Prob. 18ECh. 5.6 - Prob. 19ECh. 5.6 - Prob. 20ECh. 5.6 - Surface Area Use the Midpoint Rule to estimate the...Ch. 5.6 - Surface Area Use the Midpoint Rule to estimate the...Ch. 5.6 - Prob. 31ECh. 5.6 - Prob. 33ECh. 5 - Finding Indefinite Integrals In Exercises 114,...Ch. 5 - Prob. 2RECh. 5 - Prob. 3RECh. 5 - Prob. 4RECh. 5 - Prob. 5RECh. 5 - Prob. 6RECh. 5 - Finding Indefinite Integrals In Exercises 114,...Ch. 5 - Prob. 8RECh. 5 - Prob. 9RECh. 5 - Prob. 10RECh. 5 - Prob. 11RECh. 5 - Prob. 12RECh. 5 - Prob. 13RECh. 5 - Finding Indefinite Integrals In Exercises 114,...Ch. 5 - Prob. 15RECh. 5 - Prob. 16RECh. 5 - Prob. 17RECh. 5 - Prob. 18RECh. 5 - Prob. 19RECh. 5 - Revenue A company produces a new product for which...Ch. 5 - Prob. 21RECh. 5 - Prob. 22RECh. 5 - Prob. 23RECh. 5 - Prob. 24RECh. 5 - Prob. 25RECh. 5 - Prob. 26RECh. 5 - Prob. 27RECh. 5 - Prob. 28RECh. 5 - Prob. 29RECh. 5 - Prob. 30RECh. 5 - Prob. 31RECh. 5 - Prob. 32RECh. 5 - Production The rate of change of the output of a...Ch. 5 - Prob. 34RECh. 5 - Prob. 35RECh. 5 - Prob. 36RECh. 5 - Prob. 37RECh. 5 - Prob. 38RECh. 5 - Prob. 39RECh. 5 - Prob. 40RECh. 5 - Prob. 41RECh. 5 - Prob. 42RECh. 5 - Prob. 43RECh. 5 - Prob. 44RECh. 5 - Prob. 45RECh. 5 - Prob. 46RECh. 5 - Prob. 47RECh. 5 - Prob. 48RECh. 5 - Prob. 49RECh. 5 - Prob. 50RECh. 5 - Prob. 51RECh. 5 - Prob. 52RECh. 5 - Prob. 53RECh. 5 - Prob. 54RECh. 5 - Prob. 55RECh. 5 - Prob. 56RECh. 5 - Prob. 57RECh. 5 - Prob. 58RECh. 5 - Prob. 59RECh. 5 - Prob. 60RECh. 5 - Evaluating a Definite Integral In Exercises 5970,...Ch. 5 - Prob. 62RECh. 5 - Prob. 63RECh. 5 - Prob. 64RECh. 5 - Prob. 65RECh. 5 - Prob. 66RECh. 5 - Prob. 67RECh. 5 - Prob. 68RECh. 5 - Prob. 69RECh. 5 - Prob. 70RECh. 5 - Prob. 71RECh. 5 - Prob. 72RECh. 5 - Prob. 73RECh. 5 - Prob. 74RECh. 5 - Prob. 75RECh. 5 - Prob. 76RECh. 5 - Prob. 77RECh. 5 - Prob. 78RECh. 5 - Prob. 79RECh. 5 - Prob. 80RECh. 5 - Prob. 81RECh. 5 - Prob. 82RECh. 5 - Prob. 83RECh. 5 - Prob. 84RECh. 5 - Prob. 85RECh. 5 - Prob. 86RECh. 5 - Prob. 87RECh. 5 - Prob. 88RECh. 5 - Prob. 89RECh. 5 - Prob. 90RECh. 5 - Prob. 91RECh. 5 - Prob. 92RECh. 5 - Prob. 93RECh. 5 - Prob. 94RECh. 5 - Prob. 95RECh. 5 - Consumer and Producer Surpluses In Exercises...Ch. 5 - Prob. 97RECh. 5 - Prob. 98RECh. 5 - Prob. 99RECh. 5 - Prob. 100RECh. 5 - Prob. 101RECh. 5 - Prob. 102RECh. 5 - Prob. 103RECh. 5 - Approximating the Area of a Plane Region In...Ch. 5 - Prob. 105RECh. 5 - Prob. 106RECh. 5 - Prob. 107RECh. 5 - Prob. 108RECh. 5 - Prob. 109RECh. 5 - Prob. 110RECh. 5 - Prob. 111RECh. 5 - Prob. 112RECh. 5 - Prob. 113RECh. 5 - Prob. 114RECh. 5 - Surface Area Use the Midpoint Rule to estimate the...Ch. 5 - Prob. 1TYSCh. 5 - Prob. 2TYSCh. 5 - Prob. 3TYSCh. 5 - Take this test as you would take a test in class....Ch. 5 - Prob. 5TYSCh. 5 - Prob. 6TYSCh. 5 - Prob. 7TYSCh. 5 - Prob. 8TYSCh. 5 - Prob. 9TYSCh. 5 - Prob. 10TYSCh. 5 - Prob. 11TYSCh. 5 - Prob. 12TYSCh. 5 - Prob. 13TYSCh. 5 - Prob. 14TYSCh. 5 - Prob. 15TYSCh. 5 - Prob. 16TYSCh. 5 - Prob. 17TYSCh. 5 - Prob. 18TYSCh. 5 - Prob. 19TYSCh. 5 - Prob. 20TYSCh. 5 - Prob. 21TYSCh. 5 - Prob. 22TYS
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- Computing areas Use a double integral to find the area of thefollowing region. The region bounded by the cardioid r = 2(1 - sin θ)arrow_forwardCalculus Find the area under a curve define by the equation 5x^(4)+3x+7 between the x values 0 and 4 .arrow_forwardIntegration techniques Use the methods introduced evaluate the following integrals.arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning

Calculus: Early Transcendentals
Calculus
ISBN:9781285741550
Author:James Stewart
Publisher:Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:9780134438986
Author:Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:9780134763644
Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:9781319050740
Author:Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:W. H. Freeman


Calculus: Early Transcendental Functions
Calculus
ISBN:9781337552516
Author:Ron Larson, Bruce H. Edwards
Publisher:Cengage Learning
Definite Integral Calculus Examples, Integration - Basic Introduction, Practice Problems; Author: The Organic Chemistry Tutor;https://www.youtube.com/watch?v=rCWOdfQ3cwQ;License: Standard YouTube License, CC-BY