
College Physics
11th Edition
ISBN: 9781305952300
Author: Raymond A. Serway, Chris Vuille
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Concept explainers
Textbook Question
Chapter 5, Problem 86AP
Two blocks, A and B (with mass 50.0 kg and 1.00 × 102 kg, respectively), are connected by a string, as shown in Figure P5.86. The pulley is frictionless and of negligible mass. The coefficient of kinetic friction between block A and the incline is μk = 0.250. Determine the change in the kinetic energy of block A as it moves from  to
to  , a distance of 20.0 m up the incline (and block B drops downward a distance of 20.0 m) if the system starts from rest.
, a distance of 20.0 m up the incline (and block B drops downward a distance of 20.0 m) if the system starts from rest.
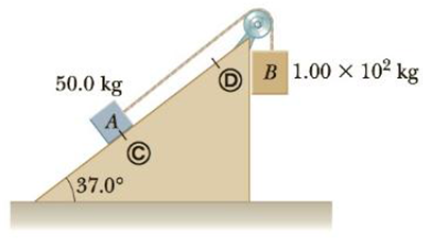
Figure P5.86
Expert Solution & Answer
Trending nowThis is a popular solution!

Chapter 5 Solutions
College Physics
Ch. 5.1 - In Figure 5.5 (a)-(d), a block moves to the right...Ch. 5.2 - A block slides at constant speed down a ramp while...Ch. 5.3 - Three identical halls are thrown from the top of a...Ch. 5.3 - Bob, of mass m, drops from a tree limb at the same...Ch. 5.5 - Calculate the elastic potential energy of a spring...Ch. 5.5 - True or False: The elastic potential energy of a...Ch. 5.5 - Elastic potential energy depends on the spring...Ch. 5.6 - A book of mass in is projected with a speed v...Ch. 5 - Consider a tug-of-war as in Figure CQ5.1, in which...Ch. 5 - Choose the best answer. A car traveling at...
Ch. 5 - (a) If the height of a playground slide is kept...Ch. 5 - (a) Can the kinetic energy of a system be...Ch. 5 - Two toboggans (with riders) of the same mass are...Ch. 5 - A bowling ball is suspended from the ceiling of a...Ch. 5 - As a mass tied to the end of a string strings from...Ch. 5 - Discuss whether any work is being done by each of...Ch. 5 - When a punter kicks a football, is he doing any...Ch. 5 - The driver of a car slams on her brakes to avoid...Ch. 5 - A weight is connected to a spring that is...Ch. 5 - For each of the situations given, state whether...Ch. 5 - Suppose you are reshelving books in a library. As...Ch. 5 - Two stones, one with twice the mass of the other,...Ch. 5 - An Earth satellite is in a circular orbit at an...Ch. 5 - Mark and David are loading identical cement blocks...Ch. 5 - If the speed of a particle is doubled, what...Ch. 5 - A certain truck has twice the mass of a car. Both...Ch. 5 - If the net work done on a particle is zero, which...Ch. 5 - A car accelerates uniformly from rest. Ignoring...Ch. 5 - A weight lifter lifts a 350-N set of weights from...Ch. 5 - In 1990 Walter Arfeuille of Belgium lifted a...Ch. 5 - A cable exerts a constant upward tension of...Ch. 5 - a shopper in a supermarket pushes a cart with a...Ch. 5 - Starting from rest, a 5.00-kg block slides 2.50 m...Ch. 5 - A horizontal force of 150 N is used to push a...Ch. 5 - A tension force of 175 N inclined at 20.0 above...Ch. 5 - A block of mass m = 2.50 kg is pushed a distance d...Ch. 5 - A mechanic pushes a 2.50 103-kg car from rest to...Ch. 5 - A 7.00-kg bowling ball moves at 3.00 m/s. How fast...Ch. 5 - A 65.0-kg runner has a speed of 5.20 m/s at one...Ch. 5 - A worker pushing a 35.0-kg wooden crate at a...Ch. 5 - A 70-kg base runner begins his slide into second...Ch. 5 - A 62.0-kg cheetah accelerates from rest to its top...Ch. 5 - A 7.80-g bullet moving at 575 m/s penetrates a...Ch. 5 - A 0.60-kg particle has a speed of 2.0 m/s at point...Ch. 5 - A large cruise ship of mass 6.50 107 kg has a...Ch. 5 - A man pushing a crate of mass m = 92.0 kg at a...Ch. 5 - A 0.20-kg stone is held 1.3 m above the top edge...Ch. 5 - When a 2.50-kg object is hung vertically on a...Ch. 5 - A block of mass 3.00 kg is placed against a...Ch. 5 - A 60.0-kg athlete leaps straight up into the air...Ch. 5 - A 2.10 103-kg pile driver is used to drive a...Ch. 5 - Two blocks are connected by a light string that...Ch. 5 - A daredevil on a motorcycle leaves the end of a...Ch. 5 - Truck suspensions often have helper springs dial...Ch. 5 - The chin-up is one exercise that can be used to...Ch. 5 - A flea is able to jump about 0.5 m. It has been...Ch. 5 - A 50.0-kg projectile is fired at an angle of 30.0...Ch. 5 - A projectile of mass m is fired horizontally with...Ch. 5 - A horizontal spring attached to a wall has a force...Ch. 5 - A 50.-kg pole vaulter running at 10. m/s vaults...Ch. 5 - A child and a sled with a combined mass of 50.0 kg...Ch. 5 - A 35.0-cm long spring is hung vertically from a...Ch. 5 - A 0.250-kg block along a horizontal track has a...Ch. 5 - A block of mass m = 5.00 kg is released from rest...Ch. 5 - Tarzan savings on a 30.0-m-long vine initially...Ch. 5 - Two blocks are connected by a light string that...Ch. 5 - The launching mechanism of a toy gun consists of a...Ch. 5 - (a) A block with a mass m is pulled along a...Ch. 5 - (a) A child slides down a water slide at an...Ch. 5 - An airplane of mass 1.50 104 kg is moving at 60.0...Ch. 5 - The system shown in Figure P5.43 is used to lift...Ch. 5 - A 25.0-kg child on a 2.00-m-long swing is released...Ch. 5 - A 2.1 103-kg car starts from rest at the top of a...Ch. 5 - A child of mass m starts from rest and slides...Ch. 5 - A skier starts from rest at the top of a hill that...Ch. 5 - In a circus performance, a monkey is strapped to a...Ch. 5 - An 80.0-kg skydiver jumps out of a balloon at an...Ch. 5 - Q A skier of mass 70.0 kg is pulled up a slope by...Ch. 5 - What average mechanical power must a 70.0-kg...Ch. 5 - While running, a person dissipates about 0.60 J of...Ch. 5 - The electric motor of a model train accelerates...Ch. 5 - When an automobile moves with constant speed down...Ch. 5 - Under normal conditions the human heart converts...Ch. 5 - Prob. 56PCh. 5 - A 1.50 103-kg car starts from rest and...Ch. 5 - A 6.50 102-kg elevator starts from rest and moves...Ch. 5 - The force acting on a particle varies as in Figure...Ch. 5 - An object of mass 3.00 kg is subject to a force Fx...Ch. 5 - The force acting on an object is given by Fx = (8x...Ch. 5 - An outfielder throws a 0.150-kg baseball at a...Ch. 5 - A roller-coaster car of mass 1.50 103 kg is...Ch. 5 - A ball of mass m = 1.80 kg is released from rest...Ch. 5 - An archer pulls her bowstring back 0.400 m by...Ch. 5 - A block of mass 12.0 kg slides from rest down a...Ch. 5 - (a) A 75-kg man steps out a window and falls (from...Ch. 5 - A toy gun uses a spring to project a 5.3-g soft...Ch. 5 - Two objects (m1 = 5.00 kg and m2 = 3.00 kg) are...Ch. 5 - A 3.50-kN piano is lilted by three workers at...Ch. 5 - A 2.00 102-g particle is released from rest at...Ch. 5 - The particle described in Problem 71 (Fig. P5.71)...Ch. 5 - In terms of saving energy, bicycling and walking...Ch. 5 - A 50.0-kg student evaluates a weight loss program...Ch. 5 - A ski jumper starts from rest 50.0 m above the...Ch. 5 - A 5.0-kg block is pushed 3.0 m up a vertical wall...Ch. 5 - A childs pogo slick (Fig. P5.77) stores energy in...Ch. 5 - A hummingbird hovers by exerting a downward force...Ch. 5 - In the dangerous sport of bungee jumping, a daring...Ch. 5 - Apollo 14 astronaut Alan Shepard famously took two...Ch. 5 - A truck travels uphill with constant velocity on a...Ch. 5 - As a 75.0-kg man steps onto a bathroom scale, the...Ch. 5 - Prob. 83APCh. 5 - A cat plays with a toy mouse suspended from a...Ch. 5 - Three objects with masses m1 = 5.00 kg, m2 = 10.0...Ch. 5 - Two blocks, A and B (with mass 50.0 kg and 1.00 ...
Additional Science Textbook Solutions
Find more solutions based on key concepts
Is Earths inner core solid and the outer core liquid because the inner core is cooler than the outer core? Expl...
Conceptual Integrated Science
42. * Insulating a house You insulate your house using insulation rated as R-12, which will conduct 1/12 Btu/h ...
College Physics
The temperature of the Universe at recombination was about 3000 K. Use Wien’s law to calculate the peak wavelen...
Loose Leaf For Explorations: Introduction To Astronomy
56. Global Positioning System. Learn more about the global positioning system and its uses. Write a short repo...
The Cosmic Perspective (8th Edition)
What is the maximum magnetic intensity in a plane electromagnetic wave whose maximum electric intensity is 100 ...
Introduction To Health Physics
An aluminum calorimeter with a mass of 100 g contains 250 g of water. The calorimeter and water are in thermal ...
Physics for Scientists and Engineers
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, physics and related others by exploring similar questions and additional content below.Similar questions
- The system shown in Figure P5.43 is used to lift an object of mass m = 76.0 kg. A constant downward force of magnitude F is applied to the loose end of the rope such that the hanging object moves upward at constant speed. Neglecting the masses of the rope and pulleys, find (a) the required value of F, (b) the tensions T1, T2, and T3, and (c) the work done by the applied force in raising the object a distance of 1.80 m. Figure P5.43arrow_forwardA block of mass m = 2.50 kg is pushed a distance d = 2.20 m along a frictionless horizontal table by a constant applied force of magnitude F = 16.0 N directed at an angle = 25.0 below the horizontal as shown in Figure P5.8. Determine the work done by (a) the applied force, (b) the normal force exerted by the table, (c) the force of gravity, and (d) the net force on the block. Figure P5.8arrow_forwardA block of mass m = 5.00 kg is released from rest from point and slides on the frictionless track shown in Figure P5.36. Determine (a) the blocks speed at points and and (b) the net work done by the gravitational force on the block as it moves from point from to . Figure P5.36arrow_forward
- A block of mass m = 2.50 kg is pushed a distance d = 2.20 m along a frictionless, horizontal table by a constant applied force of magnitude F = 16.0 N directed at an angle = 25.0 below the horizontal as shown in Figure P6.3. Determine the work done on the block by (a) the applied force, (b) the normal force exerted by the table, (c) the gravitational force, and (d) the net force on the block. Figure P6.3arrow_forwardThe system shown in Figure P5.43 is used to lift an object of mass m = 76.0 kg. A constant downward force of magnitude F is applied to the loose end of the rope such that the hanging object moves upward at constant speed. Neglecting the masses of the rope and pulleys, find (a) the required value of F, (b) the tensions T1, T2, and T3, and (c) the work done by the applied force in raising the object a distance of 1.80 m. Figure P5.43arrow_forwardA child of mass m starts from rest and slides without friction from a height h along a curved waterslide (Fig. P5.46). She is launched from a height h/5 into the pool. (a) Is mechanical energy conserved? Why? (b) Give the gravitational potential energy associated with the child and her kinetic energy in terms of mgh at the following positions: the top of the waterslide, the launching point, and the point where she lands in the pool. (c) Determine her initial speed V0 at the launch point in terms of g and h. (d) Determine her maximum airborne height ymax in terms of h, g, and the horizontal speed at that height, v0x. (e) Use the x-component of the answer to part (c) to eliminate from the answer to part (d), giving the height ymax in terms of g, h, and the launch angle . (f) Would your answers be the same if the waterslide were not frictionless? Explain. Figure P5.46arrow_forward
- A boy starts at rest and slides down a frictionless slide as in Figure P5.64. The bottom of the track is a height h above the ground. The boy then leaves the track horizontally, striking the ground a distance d as shown. Using energy methods, determine the initial height H of the boy in terms of h and d. Figure P5.64arrow_forwardAs a young man, Tarzan climbed up a vine to reach his tree house. As he got older, he decided to build and use a staircase instead. Since the work of the gravitational force mg is path Independent, what did the King of the Apes gain in using stairs?arrow_forwardA block of mass m = 2.50 kg is pushed a distance d = 2.20 m along a frictionless, horizontal table by a constant applied force of magnitude F = 16.0 N directed at ail angle = 25 below the horizontal as shown in Figure P7.5. Determine the work done on the block by (a) the applied force, (b) the normal force exerted by the table, (c) the gravitational force, and (d) the net force on the block.arrow_forward
- A block of mass m = 5.00 kg is released from rest from point and slides on the frictionless track shown in Figure P5.36. Determine (a) the blocks speed at points and and (b) the net work done by the gravitational force on the block as it moves from point from to . Figure P5.36arrow_forwardA 5.0-kg block is pushed 3.0 m up a vertical wall with constant speed by a constant force of magnitude F applied at an angle of = 30 with the horizontal, as shown in Figure P5.76. If the coefficient of kinetic friction between block and wall is 0.30, determine the work done by (a) , (b) the force of gravity, and (c) the normal force between block and wall, (d) By how much does the gravitational potential energy increase during the blocks motion? Figure P5.76arrow_forwardThe force acting on a particle varies as shown in Figure P6.14. Find the work done by the force on the particle as it moves (a) from x = 0 to x = 8.00 m, (b) from x = 8.00 m to x= 10.0 m, and (c) from x = 0 to x = 10.0 m.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
 College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University
University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning College PhysicsPhysicsISBN:9781938168000Author:Paul Peter Urone, Roger HinrichsPublisher:OpenStax College
College PhysicsPhysicsISBN:9781938168000Author:Paul Peter Urone, Roger HinrichsPublisher:OpenStax College

College Physics
Physics
ISBN:9781285737027
Author:Raymond A. Serway, Chris Vuille
Publisher:Cengage Learning

College Physics
Physics
ISBN:9781305952300
Author:Raymond A. Serway, Chris Vuille
Publisher:Cengage Learning

University Physics Volume 1
Physics
ISBN:9781938168277
Author:William Moebs, Samuel J. Ling, Jeff Sanny
Publisher:OpenStax - Rice University

Physics for Scientists and Engineers: Foundations...
Physics
ISBN:9781133939146
Author:Katz, Debora M.
Publisher:Cengage Learning

Principles of Physics: A Calculus-Based Text
Physics
ISBN:9781133104261
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning

College Physics
Physics
ISBN:9781938168000
Author:Paul Peter Urone, Roger Hinrichs
Publisher:OpenStax College
Kinetic Energy and Potential Energy; Author: Professor Dave explains;https://www.youtube.com/watch?v=g7u6pIfUVy4;License: Standard YouTube License, CC-BY