Mathematical Excursions (MindTap Course List)
4th Edition
ISBN: 9781305965584
Author: Richard N. Aufmann, Joanne Lockwood, Richard D. Nation, Daniel K. Clegg
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 5.2, Problem 28ES
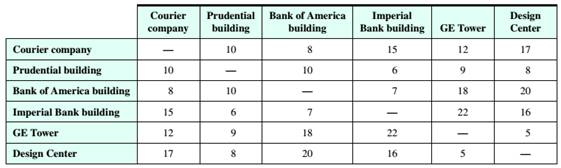
Route Planning A bike messenger needs to deliver packages to five different buildings and return to the courier company. The estimated biking times (in minutes) between the buildings are given in the following table. Use the greedy algorithm and the edge-picking algorithm to find two possible routes for the messenger to follow that Will help minimize the total travel time.
Expert Solution & Answer
Trending nowThis is a popular solution!
Students have asked these similar questions
Please provide an easy way to solve it correctly.
List each vertex using the transverse algorithm pre-order, post-order and in-order
Otitis media, or middle ear infection, is initially treated with an antibiotic. Researchers have compared two antibiotics, A and B, for their cost effectiveness. A is inexpensive, safe, and effective. B is also safe. However, it is considerably more expensive and it is generally more effective. Use the tree diagram to the right (where the costs are estimated as the total cost of medication, office visit, ear check, and hours of lost work) to answer the following.
a. Find the expected cost of using each antibiotic to treat a middle ear infection.
A tree diagram has a root that splits into 2 branches labeled A and B. Primary branch A splits into 2 secondary branches labeled 0.80 Cure 59.30 dollars and 0.20 No cure 96.15 dollars. Primary branch B splits into two secondary branches labeled 0.90 Cure 69.15 dollars and 0.10 No cure 106.00 dollars.0.800.200.900.10
b. To minimize the total expected cost, which antibiotic should be chosen?
a. The expected cost of…
Chapter 5 Solutions
Mathematical Excursions (MindTap Course List)
Ch. 5.1 - A pen-tracing puzzle is given. See if you can find...Ch. 5.1 - A pen-tracing puzzle is given. See if you can find...Ch. 5.1 - A pen-tracing puzzle is given. See if you can find...Ch. 5.1 - A pen-tracing puzzle is given. See if you can find...Ch. 5.1 - Explain why the following pen-tracing puzzle is...Ch. 5.1 - Transportation An X in the table below indicates a...Ch. 5.1 - Transportation The table below shows the nonstop...Ch. 5.1 - Social Network A group of friends is represented...Ch. 5.1 - Prob. 4ESCh. 5.1 - Determine (a) the number of edges in the graph,...
Ch. 5.1 - Determine (a) the number of edges in the graph,...Ch. 5.1 - Determine (a) the number of edges in the graph,...Ch. 5.1 - Determine (a) the number of edges in the graph,...Ch. 5.1 - Determine whether the two graphs are equivalent.Ch. 5.1 - Determine whether the two graphs are equivalent.Ch. 5.1 - Determine whether the two graphs are equivalent.Ch. 5.1 - Determine whether the two graphs are equivalent.Ch. 5.1 - Explain why the following two graphs cannot be...Ch. 5.1 - Label the vertices of the second graph so that it...Ch. 5.1 - (a) determine whether the graph is Eulerian. If it...Ch. 5.1 - (a) determine whether the graph is Eulerian. If it...Ch. 5.1 - (a) determine whether the graph is Eulerian. If it...Ch. 5.1 - (a) determine whether the graph is Eulerian. If it...Ch. 5.1 - (a) determine whether the graph is Eulerian. If it...Ch. 5.1 - (a) determine whether the graph is Eulerian. If it...Ch. 5.1 - (a) determine whether the graph is Eulerian. If it...Ch. 5.1 - (a) determine whether the graph is Eulerian. If it...Ch. 5.1 - Parks in Exercises 23 and 24, a map of a park is...Ch. 5.1 - Parks in Exercises 23 and 24, a map of a park is...Ch. 5.1 - Transportation For the train routes given in...Ch. 5.1 - Transportation For the direct air flights given in...Ch. 5.1 - Pets The diagram below shows the arrangement of a...Ch. 5.1 - Transportation A subway map is shown below. Is it...Ch. 5.1 - Prob. 29ESCh. 5.1 - Prob. 30ESCh. 5.1 - Degrees of Separation In the graph below, an edge...Ch. 5.1 - Social Network In the graph below, an edge...Ch. 5.1 - Prob. 33ESCh. 5.1 - Travel A map of South America is shown at the...Ch. 5.2 - Continue investigating Hamiltonian circuits in...Ch. 5.2 - Use the greedy algorithm and the weighted graph...Ch. 5.2 - Use the edge-picking algorithm to find a...Ch. 5.2 - Use Dirac's theorem to verify that the graph is...Ch. 5.2 - Use Dirac's theorem to verify that the graph is...Ch. 5.2 - Use Dirac's theorem to verify that the graph is...Ch. 5.2 - Use Dirac's theorem to verify that the graph is...Ch. 5.2 - Transportation For the train routes given in...Ch. 5.2 - Transportation For the direct air flights given in...Ch. 5.2 - Use trial and error to find two Hamiltonian...Ch. 5.2 - Use trial and error to find two Hamiltonian...Ch. 5.2 - Use trial and error to find two Hamiltonian...Ch. 5.2 - Use trial and error to find two Hamiltonian...Ch. 5.2 - Use the greedy algorithm to find a Hamiltonian...Ch. 5.2 - Use the greedy algorithm to find a Hamiltonian...Ch. 5.2 - Use the greedy algorithm to find a Hamiltonian...Ch. 5.2 - Use the greedy algorithm to find a Hamiltonian...Ch. 5.2 - Use the edge-picking algorithm to find a...Ch. 5.2 - Use the edge-picking algorithm to find a...Ch. 5.2 - Use the edge-picking algorithm to find a...Ch. 5.2 - Use the edge-picking algorithm to find a...Ch. 5.2 - Travel A company representative lives in...Ch. 5.2 - Travel A tourist is staying in Toronto, Canada,...Ch. 5.2 - Travel Use the edge-picking algorithm to design a...Ch. 5.2 - Travel Use the edge-picking algorithm to design a...Ch. 5.2 - Travel Nicole wants to tour Asia. She will start...Ch. 5.2 - Travel The prices for traveling between five...Ch. 5.2 - Travel Use the edge-picking algorithm to find a...Ch. 5.2 - Travel Use the edge-picking algorithm to find a...Ch. 5.2 - Route Planning Brian needs to visit the pet store,...Ch. 5.2 - Route Planning A bike messenger needs to deliver...Ch. 5.2 - Scheduling A research company has a large...Ch. 5.2 - Computer Networks A small office wishes to network...Ch. 5.2 - Route Planning A security officer patrolling a...Ch. 5.2 - Route Planning A city engineer needs to inspect...Ch. 5.2 - Draw a connected graph with six vertices that has...Ch. 5.2 - Assign weights to the edges of the following...Ch. 5.3 - The tetrahedron in figure 5.20 consists of four...Ch. 5.3 - The following graph is the projection of one ofthe...Ch. 5.3 - Prob. 3EECh. 5.3 - Give a reason why the graph below Cannot be the...Ch. 5.3 - Prob. 1ESCh. 5.3 - Prob. 2ESCh. 5.3 - Prob. 3ESCh. 5.3 - Prob. 4ESCh. 5.3 - Prob. 5ESCh. 5.3 - Prob. 6ESCh. 5.3 - Prob. 7ESCh. 5.3 - Prob. 8ESCh. 5.3 - Prob. 9ESCh. 5.3 - Prob. 10ESCh. 5.3 - Prob. 11ESCh. 5.3 - Prob. 12ESCh. 5.3 - Show that the following graph contracts to K5.Ch. 5.3 - Show that the following graph contracts to the...Ch. 5.3 - Prob. 15ESCh. 5.3 - Prob. 16ESCh. 5.3 - Prob. 17ESCh. 5.3 - Count the number of vertices, edges, and faces,...Ch. 5.3 - Count the number of vertices, edges, and faces,...Ch. 5.3 - Count the number of vertices, edges, and faces,...Ch. 5.3 - Count the number of vertices, edges, and faces,...Ch. 5.3 - Count the number of vertices, edges, and faces,...Ch. 5.3 - Prob. 23ESCh. 5.3 - Prob. 24ESCh. 5.3 - Prob. 25ESCh. 5.3 - Prob. 26ESCh. 5.3 - Prob. 27ESCh. 5.3 - Prob. 28ESCh. 5.3 - Prob. 29ESCh. 5.3 - Prob. 30ESCh. 5.4 - A one-way road ends at a two-way street. The...Ch. 5.4 - A one-way road intersects a two-way road in a...Ch. 5.4 - A two-way road intersects another two-way road in...Ch. 5.4 - Prob. 1ESCh. 5.4 - Prob. 2ESCh. 5.4 - Prob. 3ESCh. 5.4 - Prob. 4ESCh. 5.4 - Prob. 5ESCh. 5.4 - Prob. 6ESCh. 5.4 - Prob. 7ESCh. 5.4 - Prob. 8ESCh. 5.4 - Prob. 9ESCh. 5.4 - Prob. 10ESCh. 5.4 - Prob. 11ESCh. 5.4 - Prob. 12ESCh. 5.4 - Prob. 13ESCh. 5.4 - Prob. 14ESCh. 5.4 - Prob. 15ESCh. 5.4 - Prob. 16ESCh. 5.4 - Prob. 17ESCh. 5.4 - Prob. 18ESCh. 5.4 - Prob. 19ESCh. 5.4 - Prob. 20ESCh. 5.4 - Prob. 21ESCh. 5.4 - Prob. 22ESCh. 5.4 - Scheduling Six different groups of children would...Ch. 5.4 - Scheduling Five different charity organizations...Ch. 5.4 - Scheduling Students in a film class have...Ch. 5.4 - Animal Housing A researcher has discovered six new...Ch. 5.4 - Prob. 27ESCh. 5.4 - Prob. 28ESCh. 5.4 - Prob. 29ESCh. 5.4 - Prob. 30ESCh. 5.4 - Scheduling Edge colorings, as explained in...Ch. 5 - (a) determine the number of edges in the graph,...Ch. 5 - (a) determine the number of edges in the graph,...Ch. 5 - Soccer In the table below, an X indicates teams...Ch. 5 - Each vertex in the graph at the left represents a...Ch. 5 - Determine whether the two graphs are equivalent.Ch. 5 - Determine whether the two graphs are equivalent.Ch. 5 - Find an Euler path if possible, and (b) find an...Ch. 5 - Find an Euler path if possible, and (b) find an...Ch. 5 - Find an Euler path if possible, and (b) find an...Ch. 5 - Prob. 10RECh. 5 - Prob. 11RECh. 5 - Architecture The floor plan of a sculpture gallery...Ch. 5 - Use Dirac's theorem to verify that the graph is...Ch. 5 - Use Dirac's theorem to verify that the graph is...Ch. 5 - Prob. 15RECh. 5 - Prob. 16RECh. 5 - Use the greedy algorithm to find a Hamiltonian...Ch. 5 - Use the greedy algorithm to find a Hamiltonian...Ch. 5 - Use the edge-picking algorithm to find a...Ch. 5 - Use the edge-picking algorithm to find a...Ch. 5 - Efficient Route The distances, in miles, between...Ch. 5 - Computer Networking A small office needs to...Ch. 5 - Prob. 23RECh. 5 - Prob. 24RECh. 5 - Prob. 25RECh. 5 - Prob. 26RECh. 5 - Count the number of vertices, edges, and faces in...Ch. 5 - Count the number of vertices, edges, and faces in...Ch. 5 - Prob. 29RECh. 5 - Prob. 30RECh. 5 - Prob. 31RECh. 5 - Prob. 32RECh. 5 - Prob. 33RECh. 5 - Prob. 34RECh. 5 - Scheduling A company has scheduled a retreat at a...Ch. 5 - Social Network Each vertex in the graph at the...Ch. 5 - Determine whether the following two graphs are...Ch. 5 - Answer the following questions for the graph shown...Ch. 5 - Recreation The illustration below depicts bridges...Ch. 5 - a. What does Dirac's theorem state? Explain how it...Ch. 5 - Low-Cost Route The table below shows the cost of...Ch. 5 - Use the greedy algorithm to find a Hamiltonian...Ch. 5 - Prob. 8TCh. 5 - Answer the following questions for the graph shown...Ch. 5 - Prob. 10TCh. 5 - Prob. 11TCh. 5 - A group of eight friends is planning a vacation in...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- Otitis media, or middle ear infection, is initially treated with an antibiotic. Researchers have compared two antibiotics, A and B, for their cost effectiveness. A is inexpensive, safe, and effective. B is also safe. However, it is considerably more expensive and it is generally more effective. Use the tree diagram to the right (where the costs are estimated as the total cost of medication, office visit, ear check, and hours of lost work) to answer the following. a. Find the expected cost of using each antibiotic to treat a middle ear infection. b. To minimize the total expected cost, which antibiotic should be chosen? a. The expected cost of using antibiotic A is S (Round to the nearest cent as needed.) D w an example Get more help ww O Search e ( *** O 19 'C Clear all 0.70 Cure $59.30 A 0.30 No cure $96.15 0.85, Care $69.15 B 0.15 No cure $106.00 Check answer 2:17 PM 12/15/2022arrow_forwardOtitis media, or middle ear infection, is initially treated with an antibiotic. Researchers have compared two antibiotics, A and B, for their cost effectiveness. A is inexpensive, safe, and effective. B is also safe. However, it is considerably more expensive and it is generally more effective. Use the tree diagram to the right (where the costs are estimated as the total cost of medication, office visit, ear check, and hours of lost work) to answer the following. a. Find the expected cost of using each antibiotic to treat a middle ear infection. 0.75 , Cure $59.30 A 0.25 No cure $96.15 0.85, Cure $69.15 No cure $106.00 0.15 b. To minimize the total expected cost, which antibiotic should be chosen? a. The expected cost of using antibiotic A is $ (Round to the nearest cent as needed.)arrow_forwardMathematics of Graphs You are having a Christmas vacation in Europe. You want to visit these four different beautiful places and return to your hotel while minimizing your total travel time. Represent the estimated travel time between places using a weighted graph. Moreover, use the greedy algorithm and the edge-picking algorithm to find a possible route starting and ending at your hotel. The travel time is in minutes. Home Place A Place B Place C Place D Home 30 27 18 12 Place A Place B Place C 30 42 22 37 27 42 18 31 18 22 18 Place D 12 37 31 25arrow_forward
- Please, answer. Thank you!arrow_forwardDO LETTERS A & B FOR UPVOTE. PLEASE SKIP THIS IF YOU ALREADY DID THIS. THANK YOU SO MUCH. I REALLY NEED DIFFERENT ANSWERS.arrow_forward25 27 %3D Consider the graph given above. Use the nearest neighbor algorithm to find the Hamiltonian circuit starting at vertex G. a. List the vertices in the Hamiltonian circuit in the order they are visited. Do not forget to include the starting vertex at both ends. b. What is the total weight along the Hamiltonian circuit?arrow_forward
- Please solve a,b and c given in the image provided.arrow_forwardAn experiment is designed to see whether 3rd graders can write faster with a pen or pencil. Four third graders participate, 2 boys and 2 girls. For each child, a marble is drawn without replacement from a bucket containing 2 red marbles and 2 blue marbles. If a red marble is selected, the child gets a pen and if blue, the child gets a pencil. The children are assigned in this order: boy 1, girl 1, boy 2, girl 2. LetX be the number of boys assigned to a pen. Find E (X). Find SD(X). а. b.arrow_forwardA chicken farmer wishes to provide electric power to each chicken house on his farm by installing buried electrical power lines. The graph below illustrates the locations of the houses and the distances between them in feet. Use Kruskal's algorithm to determine how the farmer should dig channels in order to minimize the amount of digging. Also determine the minimum total length of channels that must be dug.arrow_forward
- ows the time al tour for A B C D A B 9 9 5 10 13 10 C D 5 13 10 10 16 16arrow_forwardRVW (Restored Volkswagens) buys 15 used VW's at each of two car auctions each week held at different locations. It then transports the cars to repair shops it contracts with. When they are restored to RVW's specifications, RVW sells 10 each to three different used car lots. There are various costs associated with the average purchase and transportation prices from each auction to each repair shop. Also there are transportation costs from the repair shops to the used car lots. RVW is concerned with minimizing its total cost given the costs in the table below. a. Given the costs below, draw a network representation for this problem. Repair Shops Used Car Lots S1 S2 L1 L2 L3 Auction 1 460 520 S1 250 300 500 Auction 2 450 500 S2 300 550 450 b. Formulate this problem as a transshipment…arrow_forwardRome Prablems 12 & 13: (R) The graph below shows 820 1070 Eurail train times in minutes 1215 Paris (P) between cities. Berlin (B) 400 650 1380 150 1530 12. Apply the Repetitive Nearest Neighbor algorithm. Answer by listing the vertices in the order you use them and the total weight of each circuit. You can write your answers in the chart below. 850 910 (M) Madrid (L) London Starting City Hamilton Circuit Total Weight Rome Paris London Madrid Berlin 13. Re-write the shortest circuit from #12 so that you depart from and return to Rome.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Glencoe Algebra 1, Student Edition, 9780079039897...
Algebra
ISBN:9780079039897
Author:Carter
Publisher:McGraw Hill
Algebra: Structure And Method, Book 1
Algebra
ISBN:9780395977224
Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. Cole
Publisher:McDougal Littell
Graph Theory: Euler Paths and Euler Circuits; Author: Mathispower4u;https://www.youtube.com/watch?v=5M-m62qTR-s;License: Standard YouTube License, CC-BY
WALK,TRIAL,CIRCUIT,PATH,CYCLE IN GRAPH THEORY; Author: DIVVELA SRINIVASA RAO;https://www.youtube.com/watch?v=iYVltZtnAik;License: Standard YouTube License, CC-BY