
Concept explainers
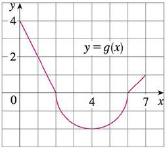
The graph of g consists of two straight lines and a semicircle. Use it to evaluate each
(a)
(b)
(c)
(a)
To evaluate: The value of the integral
Answer to Problem 32E
The value of the integral
Explanation of Solution
Given:
A graph of function
Calculation:
Show the graph for area interpretation of
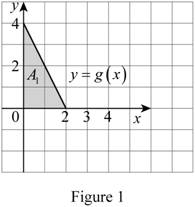
Refer to Figure 1.
The area of shaded portion is area of triangle
Calculate the value of the integral
Substitute
Thus, the value of the integral
(b)
To evaluate: The value of the integral
Answer to Problem 32E
The value of the integral
Explanation of Solution
Given:
A graph of function
Calculation:
Draw the graph for area interpretation of the integral
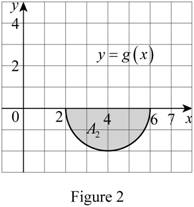
Refer to Figure 2.
The shaded portion represents area of semicircle
Consider that the area lies below x-axis. Hence,
Calculate the value of the integral
Substitute 2 for
Thus, the value of the integral
(c)
The value of the integral
Answer to Problem 32E
The value of the integral
Explanation of Solution
Draw the graph for area interpretation of the integral
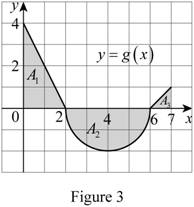
Refer to Figure 3.
The shaded portion represents area of triangle
Calculate the value of the integral
Substitute 4 for
Thus, the value of the integral
Chapter 5 Solutions
Single Variable Calculus: Concepts and Contexts, Enhanced Edition
Additional Math Textbook Solutions
Precalculus (10th Edition)
University Calculus: Early Transcendentals, Single Variable (3rd Edition)
Precalculus Enhanced with Graphing Utilities (7th Edition)
Glencoe Math Accelerated, Student Edition
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





