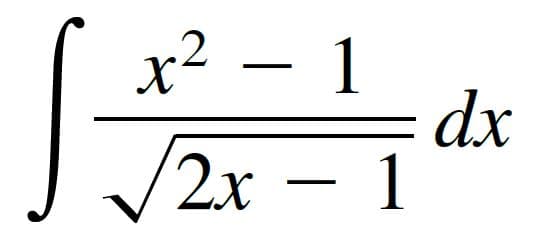1 Systems Of Linear Equations 2 Matrices 3 Determinants 4 Vector Spaces 5 Inner Product Spaces 6 Linear Transformations 7 Eigenvalues And Eigenvectors A Appendix Chapter1: Systems Of Linear Equations
1.1 Introduction To Systems Of Linear Equations 1.2 Guassian Eliminationa And Guass-jordan Elimination 1.3 Applications Of Systems Of Linear Equations 1.CR Review Exercises Section1.1: Introduction To Systems Of Linear Equations
Problem 1E: Linear Equations. In Exercises 1-6, determine whether the equation is linear in the variables x and... Problem 2E: Linear Equations. In Exercises 1-6, determine whether the equation is linear in the variables x and... Problem 3E: Linear Equations. In Exercises 1-6, determine whether the equation is linear in the variables x and... Problem 4E: Linear Equations. In Exercises 1-6, determine whether the equation is linear in the variables x and... Problem 5E: Linear Equations. In Exercises 1-6, determine whether the equation is linear in the variables x and... Problem 6E: Linear Equations. In Exercises 1-6, determine whether the equation is linear in the variables x and... Problem 7E: Parametric Representation. In Exercises 7-10, find a parametric representation of the solution set... Problem 8E: Parametric Representation. In Exercises 7-10, find a parametric representation of the solution set... Problem 9E: Parametric Representation. In Exercises 7-10, find a parametric representation of the solution set... Problem 10E: Parametric Representation. In Exercises 7-10, find a parametric representation of the solution set... Problem 11E: Graphing Analysis. In Exercises 11-24, graph the system of linear equations. Solve the system and... Problem 12E: Graphing Analysis. In Exercises 11-24, graph the system of linear equations. Solve the system and... Problem 13E: Graphing Analysis. In Exercises 11-24, graph the system of linear equations. Solve the system and... Problem 14E: Graphing Analysis. In Exercises 11-24, graph the system of linear equations. Solve the system and... Problem 15E: Graphing Analysis. In Exercises 11-24, graph the system of linear equations. Solve the system and... Problem 16E: Graphing Analysis. In Exercises 11-24, graph the system of linear equations. Solve the system and... Problem 17E: Graphing Analysis. In Exercises 11-24, graph the system of linear equations. Solve the system and... Problem 18E: Graphing Analysis. In Exercises 11-24, graph the system of linear equations. Solve the system and... Problem 19E: Graphing Analysis. In Exercises 11-24, graph the system of linear equations. Solve the system and... Problem 20E: Graphing Analysis. In Exercises 11-24, graph the system of linear equations. Solve the system and... Problem 21E: Graphing Analysis. In Exercises 11-24, graph the system of linear equations. Solve the system and... Problem 22E Problem 23E Problem 24E: Graphing Analysis. In Exercises 11-24, graph the system of linear equations. Solve the system and... Problem 25E: Back-Substitution. In Exercises 25-30, use back-substitution to solve the system. x1x2=2x2=3 Problem 26E: Back-Substitution. In Exercises 25-30, use back-substitution to solve the system. 2x14x2=63x2=9 Problem 27E: Back-Substitution. In Exercises 25-30, use back-substitution to solve the system. x+yz=02y+z=312z=0 Problem 28E: Back-Substitution. In Exercises 25-30, use back-substitution to solve the system. xy=53y+z=114z=8 Problem 29E: Back-Substitution. In Exercises 25-30, use back-substitution to solve the system.... Problem 30E: Back-Substitution. In Exercises 25-30, use back-substitution to solve the system. x1+x2+x3=0x2=0 Problem 31E Problem 32E: Graphical Analysis. In Exercises 31-36, complete parts a-e for the system of equations. a Use a... Problem 33E: Graphical Analysis. In Exercises 31-36, complete parts a-e for the system of equations. a Use a... Problem 34E Problem 35E Problem 36E: Graphical Analysis. In Exercises 31-36, complete parts a-e for the system of equations. a Use a... Problem 37E: System of Linear Equations. In Exercises 37-56, solve the system of linear equations. x1x2=03x12x2=1 Problem 38E Problem 39E: System of Linear Equations. In Exercises 37-56, solve the system of linear equations.... Problem 40E Problem 41E: System of Linear Equations. In Exercises 37-56, solve the system of linear equations.... Problem 42E: System of Linear Equations. In Exercises 37-56, solve the system of linear equations.... Problem 43E Problem 44E: System of Linear Equations. In Exercises 37-56, solve the system of linear equations.... Problem 45E: System of Linear Equations. In Exercises 37-56, solve the system of linear equations.... Problem 46E: System of Linear Equations. In Exercises 37-56, solve the system of linear equations.... Problem 47E: System of Linear Equations. In Exercises 37-56, solve the system of linear equations.... Problem 48E: System of Linear Equations. In Exercises 37-56, solve the system of linear equations.... Problem 49E: System of Linear Equations. In Exercises 37-56, solve the system of linear equations.... Problem 50E: System of Linear Equations. In Exercises 37-56, solve the system of linear equations.... Problem 51E: System of Linear Equations. In Exercises 37-56, solve the system of linear equations.... Problem 52E: System of Linear Equations. In Exercises 37-56, solve the system of linear equations.... Problem 53E: System of Linear Equations. In Exercises 37-56, solve the system of linear equations.... Problem 54E: System of Linear Equations. In Exercises 37-56, solve the system of linear equations.... Problem 55E: System of Linear Equations. In Exercises 37-56, solve the system of linear equations.... Problem 56E: System of Linear Equations. In Exercises 37-56, solve the system of linear equations.... Problem 57E: System of Linear Equations. In Exercises 57-62, use a software program or a graphing utility to... Problem 58E: System of Linear Equations. In Exercises 57-62, use a software program or a graphing utility to... Problem 59E: System of Linear Equations. In Exercises 57-62, use a software program or a graphing utility to... Problem 60E: System of Linear Equations. In Exercises 57-62, use a software program or a graphing utility to... Problem 61E: System of Linear Equations. In Exercises 57-62, use a software program or a graphing utility to... Problem 62E: System of Linear Equations. In Exercises 57-62, use a software program or a graphing utility to... Problem 63E: Number of Solutions. In Exercises 63-66, state why the system of equations must have at least one... Problem 64E: Number of Solutions. In Exercises 63-66, state why the system of equations must have at least one... Problem 65E: Number of Solutions. In Exercises 63-66, state why the system of equations must have at least one... Problem 66E: Number of Solutions. In Exercises 63-66, state why the system of equations must have at least one... Problem 67E: Nutrition One eight-ounce glass of apple juice and one eight-ounce glass of orange juice contain a... Problem 68E: Airplane Speed Two planes start from Los Angeles International Airport and fly in opposite... Problem 69E: True or False? In Exercises 69 and 70, determine whether each statement is true or false. If a... Problem 70E: True or False? In Exercises 69 and 70, determine whether each statement is true or false. If a... Problem 71E: Find a system of two equations in two variables, x1 and x2, that has the solution set given by the... Problem 72E: Find a system of two equations in three variables, x1, x2 and x3 that has the solution set given by... Problem 73E: Substitution In Exercises 73-76, solve the system of equations by first letting A=1x,B=1y, C=1z.... Problem 74E: Substitution In Exercises 73-76, solve the system of equations by first letting A=1x,B=1y, C=1z.... Problem 75E Problem 76E: Substitution In Exercises 73-76, solve the system of equations by first letting A=1x,B=1y, C=1z.... Problem 77E Problem 78E: Trigonometric Coefficients In Exercises 77 and 78, solve the system of linear equations for x and y.... Problem 79E: Coefficient Design In Exercises 79-84, determine the values of k such that the system of linear... Problem 80E: Coefficient Design In Exercises 79-84, determine the values of k such that the system of linear... Problem 81E: Coefficient Design In Exercises 79-84, determine the values of k such that the system of linear... Problem 82E: Coefficient Design In Exercises 79-84, determine the values of k such that the system of linear... Problem 83E Problem 84E: Coefficient Design In Exercises 79-84, determine the values of k such that the system of linear... Problem 85E: Determine the values of k such that the system of linear equations does not have a unique solution.... Problem 86E: CAPSTONE Find values of a, b, and c such that the system of linear equations has a exactly one... Problem 87E: Writing Consider the system of linear equations in x and y. a1x+b1y=c1a2x+b2y=c2a3x+b3y=c3 Describe... Problem 88E: Writing Explain why the system of linear equations in Exercise 87 must be consistent when the... Problem 89E: Show that if ax2+bx+c=0 for all x, then a=b=c=0. Problem 90E: Consider the system of linear equations in x and y. ax+by=ecx+dy=f Under what conditions will the... Problem 91E: Discovery In Exercises 91 and 92, sketch the lines represented by the system of equations. Then use... Problem 92E: Discovery In Exercises 91 and 92, sketch the lines represented by the system of equations. Then use... Problem 93E Problem 94E: Writing In Exercises 93 and 94, the graphs of the two equations appear to be parallel. Solve the... Problem 89E: Show that if ax2+bx+c=0 for all x, then a=b=c=0.
Related questions
Calculus 11th Edition - Ron Larson
Chapter 4.5 - Integration by Substitution
Find the indefinite integral by making a change of variables; please show steps & explain work, thank you:
Transcribed Image Text: x² – 1
dx
V2x – 1
With differentiation, one of the major concepts of calculus. Integration involves the calculation of an integral, which is useful to find many quantities such as areas, volumes, and displacement.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by step
Solved in 2 steps with 2 images