Elementary Geometry For College Students, 7e
7th Edition
ISBN: 9781337614085
Author: Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher: Cengage,
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 5.4, Problem 2E
Use theorem 5.4.2 to form a proportion in which SV is a geometric mean.
[Hint:
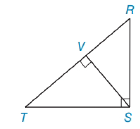
Exercises 1-6
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
T2.12 The army reports that the distribution of head cir-
cumference among male soldiers is approximately
The peak flow rate of a person is the fastest rate at which the person can expel air after taking a deep breath.Peak flow rate is measured in units of liters per minute and gives an indication of the person’s respiratoryhealth. Researchers measured peak flow rate and height for each of a sample of 17 men. The results are givenin the table. (image included)
a. Create a scatterplot displaying the relationship between peak flow rate and height.b. Calculate the sample correlation coefficient for peak flow rate and height.c. If we were to predict the peak flow rate using height with a least-squares regression model, whatis the slope estimate ˆb?d. Continuing with part a, what is the intercept estimate ˆa?e. Based on the regression model, what is the predicted peak flow rate for a subject that is 175cmtall?f. Looking at the original data, subject 8 is 175cm tall with a peak flow rate of 670l/min. What isthe residual for this subject?g. Fit the least-squares model in R. What is the…
Need help! Don’t understand..
Chapter 5 Solutions
Elementary Geometry For College Students, 7e
Ch. 5.1 - In Exercises 1 to 4, give the ratios in simplified...Ch. 5.1 - In Exercises 1 to 4, give the ratios in simplified...Ch. 5.1 - In Exercises 1 to 4, give the ratios in simplified...Ch. 5.1 - In Exercises 1 to 4, give the ratios in simplified...Ch. 5.1 - In Exercises 5 to 14, find the value of x in each...Ch. 5.1 - In Exercises 5 to 14, find the value of x in each...Ch. 5.1 - In Exercises 5 to 14, find the value of x in each...Ch. 5.1 - In Exercises 5 to 14, find the value of x in each...Ch. 5.1 - In Exercises 5 to 14, find the value of x in each...Ch. 5.1 - In Exercises 5 to 14, find the value of x in each...
Ch. 5.1 - In Exercises 5 to 14, find the value of x in each...Ch. 5.1 - In Exercises 5 to 14, find the value of x in each...Ch. 5.1 - In Exercises 5 to 14, find the value of x in each...Ch. 5.1 - In Exercises 5 to 14, find the value of x in each...Ch. 5.1 - Sarah ran the 300-m hurdles in 47.7 sec. In meters...Ch. 5.1 - Fran has been hired to sew the dance troupes...Ch. 5.1 - In Exercises 17 to 22, use proportions to solve...Ch. 5.1 - In Exercises 17 to 22, use proportions to solve...Ch. 5.1 - In Exercises 17 to 22, use proportions to solve...Ch. 5.1 - In Exercises 17 to 22, use proportions to solve...Ch. 5.1 - In Exercises 17 to 22, use proportions to solve...Ch. 5.1 - In Exercises 17 to 22, use proportions to solve...Ch. 5.1 - The salaries of a secretary, a salesperson, and a...Ch. 5.1 - The salaries of a school cook, custodian, and bus...Ch. 5.1 - If the measures of the angles of a quadrilateral...Ch. 5.1 - If the measures of the angles of a quadrilateral...Ch. 5.1 - Prob. 27ECh. 5.1 - Prob. 28ECh. 5.1 - If 1 in. equals 2.54 cm, use a proportion to...Ch. 5.1 - If 1 kg equals 2.2 lb, use a proportion to convert...Ch. 5.1 - For the quadrilaterals shown, MNWX=NPXY=PQYZ=MQWZ....Ch. 5.1 - Prob. 32ECh. 5.1 - Two numbers a and b are in the ratio 3:4. If the...Ch. 5.1 - Two numbers a and b are in the ratio 2:3. If both...Ch. 5.1 - If the ratio of the measure of the complement of...Ch. 5.1 - If the ratio of the measure of the complement of...Ch. 5.1 - On a blueprint, a 1-in. scale corresponds to 3 ft....Ch. 5.1 - To find the golden ratio see the Discover activity...Ch. 5.1 - Find a the exact length of an ideal rectangle with...Ch. 5.1 - Prove: If ab=cd where a, b, c and d are nonzero,...Ch. 5.1 - Prob. 41ECh. 5.1 - In the figure, assume that a 0. Prove that...Ch. 5.1 - In the figure, assume that a 0. Prove that...Ch. 5.2 - a What is true of any pair of corresponding angles...Ch. 5.2 - a Are any two quadrilaterals similar? b Are any...Ch. 5.2 - a Are any two regular pentagons similar? b Are any...Ch. 5.2 - a Are any two equilateral hexagons similar? b Are...Ch. 5.2 - In Exercises 5 and 6, refer to the drawing. a...Ch. 5.2 - In Exercises 5 and 6, refer to the drawing. a If...Ch. 5.2 - Prob. 7ECh. 5.2 - Given that rectangle ABCE is similar to rectangle...Ch. 5.2 - Given: MNPQRS,mM=56,mR=82,MN=9,QR=6,RS=7,MP=12...Ch. 5.2 - Given: ABCPRC,mA=67,PC=5,CR=12,PR=13,AB=26 Find: a...Ch. 5.2 - a Does the similarity relationship have a...Ch. 5.2 - Using the names of property from Exercise 11,...Ch. 5.2 - If the drawing, HJKFGK. If HK=6,KF=8, and HJ=4,...Ch. 5.2 - If the drawing, HJKFGK. If HK=6,KF=8, and FG=5,...Ch. 5.2 - Quadrilateral ABCD quadrilateral HJKL. If mA=55,...Ch. 5.2 - Quadrilateral ABCD quadrilateral HJKL. If...Ch. 5.2 - Quadrilateral ABCD quadrilateral HJKL. If...Ch. 5.2 - Quadrilateral ABCD quadrilateral HJKL. If...Ch. 5.2 - Quadrilateral ABCD quadrilateral HJKL. If...Ch. 5.2 - Quadrilateral ABCD quadrilateral HJKL. If...Ch. 5.2 - In Exercises 21 to 24, ADEABC. Given:...Ch. 5.2 - In Exercises 21 to 24, ADEABC. Given:...Ch. 5.2 - In Exercises 21 to 24, ADEABC. Given:...Ch. 5.2 - In Exercises 21 to 24, ADEABC. Given:...Ch. 5.2 - Pentagon ABCDE pentagon GHJKL not shown, AB=6, and...Ch. 5.2 - Quadrilateral MNPQ quadrilateral WXYZ not shown,...Ch. 5.2 - Prob. 27ECh. 5.2 - A technical drawing shows the 312 ft lengths of...Ch. 5.2 - In Exercises 29 to 32, use the fact that triangles...Ch. 5.2 - In Exercise 29 to 32, use the fact that triangles...Ch. 5.2 - In Exercise 29 to 32, use the fact that triangles...Ch. 5.2 - In Exercise 29 to 32, use the fact that triangles...Ch. 5.2 - In the drawing, ABDCEF with transversals l and m....Ch. 5.2 - In the drawing, ABDCEF. Suppose that transversals...Ch. 5.2 - Prob. 35ECh. 5.2 - Given RST, a second triangle (UVW) is constructed...Ch. 5.2 - Henry watches his 32 inch diagonal LCD television...Ch. 5.2 - Prob. 38ECh. 5.2 - Prob. 39ECh. 5.2 - For Exercises 39 to 40, use intuition to from a...Ch. 5.3 - What is the acronym that is used to represent each...Ch. 5.3 - Classify as true or false. a Any two rectangles...Ch. 5.3 - Classify as true or false: a If the vertex angles...Ch. 5.3 - Classify as true or false: a If the midpoints of...Ch. 5.3 - In Exercises 5 to 8, name the method...Ch. 5.3 - In Exercises 5 to 8, name the method...Ch. 5.3 - In Exercises 5 to 8, name the method...Ch. 5.3 - In Exercises 5 to 8, name the method...Ch. 5.3 - In Exercises 9 to 12, name the method that...Ch. 5.3 - In Exercises 9 to 12, name the method that...Ch. 5.3 - In Exercises 9 to 12, name the method that...Ch. 5.3 - In Exercises 9 to 12, name the method that...Ch. 5.3 - In Exercises 13 to 16, provide the missing...Ch. 5.3 - In Exercises 13 to 16, provide the missing...Ch. 5.3 - In Exercises 13 to 16, provide the missing...Ch. 5.3 - In Exercises 13 to 16, provide the missing...Ch. 5.3 - In Exercises 17 to 24, complete each proof. Given:...Ch. 5.3 - In Exercises 17 to 24, complete each proof. Given:...Ch. 5.3 - Prob. 19ECh. 5.3 - In Exercises 17 to 24, complete each proof. Given:...Ch. 5.3 - In Exercises 17 to 24, complete each proof. Given:...Ch. 5.3 - In Exercises 17 to 24, complete each proof. Given:...Ch. 5.3 - In Exercises 17 to 24, complete each proof. Given:...Ch. 5.3 - Prob. 24ECh. 5.3 - In Exercises 25 to 28, ABCDBE Exercises 25-28...Ch. 5.3 - In Exercises 25 to 28, ABCDBE Exercises 25-28...Ch. 5.3 - In Exercises 25 to 28, ABCDBE Exercises 25-28...Ch. 5.3 - In Exercises 25 to 28, ABCDBE Exercises 25-28...Ch. 5.3 - CDECBA with CDEB. If CD=10,DA=8 and CE=6, find EB....Ch. 5.3 - CDECBA with CDEB. If CD=10,CA=16 and EB=12, find...Ch. 5.3 - ABFCBD with obtuse angles at vertices D and F as...Ch. 5.3 - ABFCBD with obtuse angles at vertices D and F as...Ch. 5.3 - In Exercise 33, provide a two-column proof....Ch. 5.3 - In Exercise 34, provide a paragraph proof. Given:...Ch. 5.3 - Use a two-column proof to prove the following...Ch. 5.3 - Prob. 36ECh. 5.3 - Use the result of Exercise 13 to do the following...Ch. 5.3 - Use the result of Exercise 13 to do the following...Ch. 5.3 - The distance across a pond is to be measured...Ch. 5.3 - In the figure, ABCADB. Find AB if AD=2 and DC=6.Ch. 5.3 - Prove that the altitude drawn to the hypotenuse of...Ch. 5.3 - Prove that the line segment joining the midpoints...Ch. 5.3 - Prob. 43ECh. 5.4 - By naming the vertices in order, state three...Ch. 5.4 - Use theorem 5.4.2 to form a proportion in which SV...Ch. 5.4 - Use theorem 5.4.3 to form a proportion in which RS...Ch. 5.4 - Use theorem 5.4.3 to form a proportion in which TS...Ch. 5.4 - Use theorem 5.4.2 to find RV if SV=6 and VT=8....Ch. 5.4 - Prob. 6ECh. 5.4 - Find the length of DF if: a DE=8 and EF=6. b DE=5...Ch. 5.4 - Find the length of DE if: a DF=13 and EF=5. b...Ch. 5.4 - Find EF if: a DF=17 and DE=15. b DF=12 and DE=82....Ch. 5.4 - Find DF if: a DE=12 and EF=5 b DF=12 and EF=6....Ch. 5.4 - Determine whether each triple (a,b,c) is a...Ch. 5.4 - Prob. 12ECh. 5.4 - Prob. 13ECh. 5.4 - Determine the type of triangle represented if the...Ch. 5.4 - A guy wire 25 ft long supports an antenna at a...Ch. 5.4 - A strong wind holds a kite 30 ft above the earth...Ch. 5.4 - A boat is 6 m below the level of a pier and 12 m...Ch. 5.4 - A hot-air balloon is held in place by the ground...Ch. 5.4 - A drawbridge that is 104 ft in length is raised at...Ch. 5.4 - A drawbridge that is 136 ft in length is raised at...Ch. 5.4 - A rectangle has a width of 16 cm and a diagonal of...Ch. 5.4 - A right triangle has legs of lengths x and 2x2 and...Ch. 5.4 - A rectangle has base length x3, altitude length...Ch. 5.4 - The diagonals of a rhombus measure 6 m and 8 m....Ch. 5.4 - Each side of a rhombus measure 12 in. If one...Ch. 5.4 - An isosceles right triangle has a hypotenuse of...Ch. 5.4 - Prob. 27ECh. 5.4 - In right ABC with right C, AB=10 and BC=8. Find...Ch. 5.4 - Prob. 29ECh. 5.4 - Prob. 30ECh. 5.4 - Find the length of the altitude to the 26-in. side...Ch. 5.4 - Prob. 32ECh. 5.4 - In quadrilateral RSTU, RSST and UT diagonal RT. If...Ch. 5.4 - Prob. 34ECh. 5.4 - If a=p2q2,b=2pq and c=p2+q2, show that c2=a2+b2.Ch. 5.4 - Prob. 36ECh. 5.4 - Prob. 37ECh. 5.4 - When the rectangle in the accompanying drawing...Ch. 5.4 - A, C and F are three of the vertices of the cube...Ch. 5.4 - Prob. 40ECh. 5.4 - In the figure, square RSTV has its vertices on the...Ch. 5.4 - Prove that if (a,b,c) is a Pythagorean triple and...Ch. 5.4 - Use Figure 5.19 to prove Theorem 5.4.2. Theorem...Ch. 5.4 - Use Figures 5.20 and 5.21 to prove Lemma 5.4.3....Ch. 5.4 - Prob. 45ECh. 5.5 - For the 45-45-90 triangle shown, suppose that...Ch. 5.5 - For the 45-45-90 triangle shown, suppose that...Ch. 5.5 - For the 30-60-90 triangle shown, suppose that...Ch. 5.5 - For the 30-60-90 triangle shown, suppose that...Ch. 5.5 - In Exercises 5 to 22, find the missing lengths....Ch. 5.5 - In Exercises 5 to 22, find the missing lengths....Ch. 5.5 - In Exercises 5 to 22, find the missing lengths....Ch. 5.5 - In Exercises 5 to 22, find the missing lengths....Ch. 5.5 - In Exercises 5 to 22, find the missing lengths....Ch. 5.5 - In Exercises 5 to 22, find the missing lengths....Ch. 5.5 - In Exercises 5 to 22, find the missing lengths....Ch. 5.5 - In Exercises 5 to 22, find the missing lengths....Ch. 5.5 - In Exercises 5 to 22, find the missing lengths....Ch. 5.5 - In Exercises 5 to 22, find the missing lengths....Ch. 5.5 - Prob. 15ECh. 5.5 - Prob. 16ECh. 5.5 - Prob. 17ECh. 5.5 - In Exercises 15 to 19, create drawings as needed....Ch. 5.5 - In Exercises15 to 19, create drawing as needed....Ch. 5.5 - Given: NQM with angles as shown in the drawing...Ch. 5.5 - Given: XYZ with angles as shown in the drawing...Ch. 5.5 - Given: Rhombus ABCD not shown in which diagonals...Ch. 5.5 - Prob. 23ECh. 5.5 - To unload groceries from a delivery truck at the...Ch. 5.5 - A jogger runs along two sides of an open...Ch. 5.5 - Prob. 26ECh. 5.5 - Prob. 27ECh. 5.5 - In Exercises 27 to 33, give both exact solutions...Ch. 5.5 - Prob. 29ECh. 5.5 - Prob. 30ECh. 5.5 - In Exercises 27 to 33, give both exact solutions...Ch. 5.5 - In Exercises 27 to 33, give both exact solutions...Ch. 5.5 - In Exercises 27 to 33, give both exact solutions...Ch. 5.5 - Note: Exercises preceded by an asterisk are of a...Ch. 5.5 - In regular hexagon ABCDEF, AB=6 inches. Find the...Ch. 5.5 - In regular hexagon ABCDEF, the length of AB is x...Ch. 5.5 - In right triangle XYZ, XY=3 and YZ=4. If V is the...Ch. 5.5 - Diagonal EC separates pentagon ABCDE into square...Ch. 5.5 - For equilateral RST, RT=6. Squares and triangles...Ch. 5.6 - Note: Exercises preceded by an asterisk are of a...Ch. 5.6 - Prob. 2ECh. 5.6 - Given that ABEF=BCFG=CDGH, are the following...Ch. 5.6 - Given that XYTS, are the following proportion...Ch. 5.6 - Given: l1l2l3l4,AB=5,BC=4,CD=3,EH=10 Find:...Ch. 5.6 - Given: l1l2l3l4,AB=7,BC=5,CD=4,EF=6 Find: FG,GH,EHCh. 5.6 - Given: l1l2l3,AB=4,BC=5,DE=x,EF=12x Find: x,DE,EFCh. 5.6 - Given: l1l2l3,AB=5,BC=x,DE=x2,EF=7 Find: x,BC,DECh. 5.6 - Given: DEBC,AD=5,DB=12,AE=7 Find: ECCh. 5.6 - Given: DEBC,AD=6,DB=10,AC=20 Find: ECCh. 5.6 - Prob. 11ECh. 5.6 - Given: DEBC,AD=5,DB=a+3,AE=a+1,EC=3(a1) Find:...Ch. 5.6 - Given: RW bisects SRT Do the following equalities...Ch. 5.6 - Given: RW bisects SRT Do the following equalities...Ch. 5.6 - Given: UT bisects WUV,WU=8,UV=12,WT=6 Find: TVCh. 5.6 - Given: UT bisects WUV,WU=9,UV=12,WV=9 Find: WTCh. 5.6 - Given: NQ bisects MNP,NP=MQ,QP=8,MN=12 Find: NPCh. 5.6 - Prob. 18ECh. 5.6 - Prob. 19ECh. 5.6 - Given: In ABC,AD bisects BAC AB=20 and AC=16 Find:...Ch. 5.6 - Prob. 21ECh. 5.6 - In ABC,mCAB=80,mACB=60,andABC=40. With the angle...Ch. 5.6 - In ABC,AC=5.3,BC=7.2 and BA=6.7. With angle...Ch. 5.6 - In right RST not shown with right S,RV bisects SRT...Ch. 5.6 - Given: RV bisects SRT, RS=x6,SV=3, RT=2x, and...Ch. 5.6 - Given: MR bisects NMP, MN=2x,NR=x, RP=x+1, and...Ch. 5.6 - Given point D in the interior of RST, which...Ch. 5.6 - In RST, suppose that RH,TG, and SK are medians....Ch. 5.6 - Prob. 29ECh. 5.6 - Prob. 30ECh. 5.6 - Prob. 31ECh. 5.6 - Given: RST, with XYRT and YZRS Prove: RXXS=ZTRZCh. 5.6 - Prob. 33ECh. 5.6 - Use Exercise 33 and the following drawing to...Ch. 5.6 - Use Theorem 5.6.3 to complete the proof of this...Ch. 5.6 - In right ABC,mB=30. Also, AB=123 and AD bisects...Ch. 5.6 - Prob. 37ECh. 5.6 - In right ABC with right C,AD bisects BAC. If AC=6...Ch. 5.6 - Given: ABC not shown is isosceles with...Ch. 5.6 - Given: RST with right RST; mR=30 and ST=6; RST is...Ch. 5.6 - Prob. 41ECh. 5.6 - Prob. 42ECh. 5.CR - Prob. 1CRCh. 5.CR - Prob. 2CRCh. 5.CR - Prob. 3CRCh. 5.CR - Prob. 4CRCh. 5.CR - Prob. 5CRCh. 5.CR - Prob. 6CRCh. 5.CR - Prob. 7CRCh. 5.CR - Find the values of x in each proportion: a x6=3x c...Ch. 5.CR - Use proportions to solve Review Exercises 9 to 11....Ch. 5.CR - Prob. 10CRCh. 5.CR - Prob. 11CRCh. 5.CR - The ratio of the measures of sides of a...Ch. 5.CR - Prob. 13CRCh. 5.CR - The length of the sides of a triangle are 6, 8 and...Ch. 5.CR - The ratio of the measure of the supplement of an...Ch. 5.CR - Prob. 16CRCh. 5.CR - Given: ABCD is a parallelogram. DB intersects AE...Ch. 5.CR - Prob. 18CRCh. 5.CR - Prob. 19CRCh. 5.CR - Prob. 20CRCh. 5.CR - Prob. 21CRCh. 5.CR - Prob. 22CRCh. 5.CR - Prob. 23CRCh. 5.CR - For Review Exercises 24 to 26, GJ bisects FGH...Ch. 5.CR - For Review Exercises 24 to 26, GJ bisects FGH...Ch. 5.CR - For Review Exercises 24 to 26, GJ bisects FGH...Ch. 5.CR - Given:...Ch. 5.CR - Prove that if a line bisects one side of a...Ch. 5.CR - Prove that the diagonals of a trapezoid divide...Ch. 5.CR - Given: ABCwithrightBACADBC...Ch. 5.CR - Given: ABCwithrightBACADBC...Ch. 5.CR - Prob. 32CRCh. 5.CR - Given:...Ch. 5.CR - Find the length of a diagonal of a square whose...Ch. 5.CR - Prob. 35CRCh. 5.CR - Find the length of a side of a rhombus whose...Ch. 5.CR - Find the length of an altitude of an equilateral...Ch. 5.CR - Prob. 38CRCh. 5.CR - The length of the three sides of a triangle are...Ch. 5.CR - Prob. 40CRCh. 5.CR - Prob. 41CRCh. 5.CR - Prob. 42CRCh. 5.CT - Reduce to its simplest form: a The ratio 12:20 b...Ch. 5.CT - Prob. 2CTCh. 5.CT - Prob. 3CTCh. 5.CT - Prob. 4CTCh. 5.CT - Prob. 5CTCh. 5.CT - In right triangle ABC,CD- is the altitude from C...Ch. 5.CT - Prob. 7CTCh. 5.CT - Given its lengths of sides, is RST a right...Ch. 5.CT - Prob. 9CTCh. 5.CT - In XYZ,XZ-YZ- and Z is a right angle. a Find XY if...Ch. 5.CT - In DEF,D is a right angle and m F=30. a Find DE if...Ch. 5.CT - Prob. 12CTCh. 5.CT - In MNP,NQ bisects MNP. If PN = 6, MN = 9, and MP =...Ch. 5.CT - Prob. 14CTCh. 5.CT - Prob. 15CTCh. 5.CT - Prob. 16CTCh. 5.CT - In Exercises 16 and 17, complete the statements...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, geometry and related others by exploring similar questions and additional content below.Similar questions
- Find the values of x in each proportion: a x6=3x c 6x+4=2x+2 b x53=2x37 d x+35=x+57 e x2x5=2x+1x1 g x1x+2=103x2 f x(x+5)4x+4=95 h x+72=x+2x2arrow_forwardA piece shown by the shaded portion is to be cut from a square plate 128 millimeters on a side. a. Compute the area of the piece to be cut. Round the answer to the nearest square millimeter. b. After cutting the piece, determine the percentage of the plate that will be wasted.arrow_forwardIn Example 7, find the average speed of the car (a) from t1=0tot2=1 second and (b) from t1=1 second to t2=4 seconds.arrow_forward
- Tsunami Waves and BreakwatersThis is a continuation of Exercise 16. Breakwaters affect wave height by reducing energy. See Figure 5.30. If a tsunami wave of height H in a channel of width W encounters a breakwater that narrows the channel to a width w, then the height h of the wave beyond the breakwater is given by h=HR0.5, where R is the width ratio R=w/W. a. Suppose a wave of height 8 feet in a channel of width 5000feet encounters a breakwater that narrows the channel to 3000feet. What is the height of the wave beyond the breakwater? b. If a channel width is cut in half by a breakwater, what is the effect on wave height? 16. Height of Tsunami WavesWhen waves generated by tsunamis approach shore, the height of the waves generally increases. Understanding the factors that contribute to this increase can aid in controlling potential damage to areas at risk. Greens law tells how water depth affects the height of a tsunami wave. If a tsunami wave has height H at an ocean depth D, and the wave travels to a location with water depth d, then the new height h of the wave is given by h=HR0.25, where R is the water depth ratio given by R=D/d. a. Calculate the height of a tsunami wave in water 25feet deep if its height is 3feet at its point of origin in water 15,000feet deep. b. If water depth decreases by half, the depth ratio R is doubled. How is the height of the tsunami wave affected?arrow_forwardUse the table of values you made in part 4 of the example to find the limiting value of the average rate of change in velocity.arrow_forwardHi. PLease note I already asked this question and received the wrong answer. Jobs and productivity! How do retail stores rate? One way to answer this question is to examine annual profits per employee. The following data give annual profits per employee (in units of 1 thousand dollars per employee) for companies in retail sales. Assume σ ≈ 3.6 thousand dollars. 3.9 6.5 4.5 8.7 7.5 5.2 8.3 5.9 2.6 2.9 8.1 −1.9 11.9 8.2 6.4 4.7 5.5 4.8 3.0 4.3 −6.0 1.5 2.9 4.8 −1.7 9.4 5.5 5.8 4.7 6.2 15.0 4.1 3.7 5.1 4.2 (a) Use a calculator or appropriate computer software to find x for the preceding data. (Round your answer to two decimal places.) thousand dollars per employee(b) Let us say that the preceding data are representative of the entire sector of retail sales companies. Find an 80% confidence interval for μ, the average annual profit per employee for retail sales. (Round your answers to two decimal places.)…arrow_forward
- (c) Are your estimates in parts (a) and (b) upper and lower estimates? Ex- plain. (A) (b) is a lower estimate and (a) is an upper estimate since v is a decreasing function of t. (B) (a) is a lower estimate and (b) is an upper estimate since v is an increasing function of t. (C) (a) and (b) are neither lower nor upper estimates since v is neither an increasing nor decreasing function of t. (d) Let's find an overestimate and underestimate of the distance traveled by the motorcycle during this time period.arrow_forwardAnswer only Garrow_forwardIn the model in the table below, how is "1.3" interpreted? Model R2 Standard error y 5 + 1.3x 0.68 2.56 A) 130% of the variation in y is accounted for by x. B) On the average, the deViation of the estimated value from the actual value is 1.3. C) Whenever the value of x is 0, the value of y is 1.3. D) For every unit of change in x, there is a corresponding change in y by 1.3.arrow_forward
- Do the data in Table 1 suggest a linear relation between the pressure P and temperature T of a gas? Temperature (°C) Pressure (kPa) 40 1365.80 45 1385.40 55 1424.60 70 1483.40 80 1522.60arrow_forwardRefer to Table 2-1. The percentage or proportion associated with X = 3 is __________. Table 2-1 X f 5 1 4 2 3 4 2 1 1 2 Group of answer choices 0.10 0.30 0.20 0.40arrow_forwardFor Exercise, use the given data to find a variation model relating y to x. B х 2 12 48 2 У 0.25arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal LittellElementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Algebra: Structure And Method, Book 1
Algebra
ISBN:9780395977224
Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. Cole
Publisher:McDougal Littell
Elementary Geometry For College Students, 7e
Geometry
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Cengage,
Big Ideas Math A Bridge To Success Algebra 1: Stu...
Algebra
ISBN:9781680331141
Author:HOUGHTON MIFFLIN HARCOURT
Publisher:Houghton Mifflin Harcourt
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781337278461
Author:Ron Larson
Publisher:Cengage Learning
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Sequences and Series Introduction; Author: Mario's Math Tutoring;https://www.youtube.com/watch?v=m5Yn4BdpOV0;License: Standard YouTube License, CC-BY
Introduction to sequences; Author: Dr. Trefor Bazett;https://www.youtube.com/watch?v=VG9ft4_dK24;License: Standard YouTube License, CC-BY