
Calculus: Early Transcendentals
8th Edition
ISBN: 9781285741550
Author: James Stewart
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Concept explainers
Textbook Question
Chapter 5.4, Problem 49E
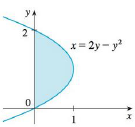
The area of the region that lies to the right of the y-axis and to the left of the parabola x = 2y − y2 (the shaded region in the figure) is given by the integral
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Chapter 5 Solutions
Calculus: Early Transcendentals
Ch. 5.1 - Prob. 1ECh. 5.1 - (a) Use six rectangles to find estimates of each...Ch. 5.1 - (a) Estimate the area under the graph of f(x) =...Ch. 5.1 - Prob. 4ECh. 5.1 - (a) Estimate the area under the graph of f(x) = 1...Ch. 5.1 - Prob. 6ECh. 5.1 - Prob. 7ECh. 5.1 - Prob. 8ECh. 5.1 - The speed of a runner increased steadily during...Ch. 5.1 - The table shows speedometer readings at 10-second...
Ch. 5.1 - Oil leaked from a tank at a rate of r(t) liters...Ch. 5.1 - When we estimate distances from velocity data, it...Ch. 5.1 - The velocity graph of a braking car is shown. Use...Ch. 5.1 - The velocity graph of a car accelerating from rest...Ch. 5.1 - In someone infected with measles, the virus level...Ch. 5.1 - The table shows the number of people per day who...Ch. 5.1 - Use Definition 2 to find an expression for the...Ch. 5.1 - Use Definition 2 to find an expression for the...Ch. 5.1 - Use Definition 2 to find an expression for the...Ch. 5.1 - Prob. 24ECh. 5.1 - Prob. 25ECh. 5.1 - (a) Use Definition 2 to find an expression for the...Ch. 5.1 - Let A be the area under the graph of an increasing...Ch. 5.1 - If A is the area under the curve y = ex from 1 to...Ch. 5.1 - (a) Let An be the area of a polygon with n equal...Ch. 5.2 - Evaluate the Riemann sum for f(x) = x 1, 6 x ...Ch. 5.2 - If f(x)=cosx0x3/4 evaluate the Riemann sum with n...Ch. 5.2 - If f(x) = x2 4, 0 x 3, find the Riemann sum...Ch. 5.2 - (a) Find the Riemann sum for f(x) = 1/x, 1 x 2,...Ch. 5.2 - The graph of a function f is given. Estimate...Ch. 5.2 - The graph of g is shown. Estimate 24g(x)dx with...Ch. 5.2 - A table of values of an increasing function f is...Ch. 5.2 - The table gives the values of a function obtained...Ch. 5.2 - Use the Midpoint Rule with the given value of n to...Ch. 5.2 - Use the Midpoint Rule with the given value of n to...Ch. 5.2 - Use the Midpoint Rule with the given value of n to...Ch. 5.2 - Use the Midpoint Rule with the given value of n to...Ch. 5.2 - With a programmable calculator or computer (see...Ch. 5.2 - Prob. 15ECh. 5.2 - Use a calculator or computer to make a table of...Ch. 5.2 - Express the limit as a definite integral on the...Ch. 5.2 - Express the limit as a definite integral on the...Ch. 5.2 - Express the limit as a definite integral on the...Ch. 5.2 - Express the limit as a definite integral on the...Ch. 5.2 - Use the form of the definition of the integral...Ch. 5.2 - Use the form of the definition of the integral...Ch. 5.2 - Use the form of the definition of the integral...Ch. 5.2 - Use the form of the definition of the integral...Ch. 5.2 - Use the form of the definition of the integral...Ch. 5.2 - (a) Find an approximation to the integral...Ch. 5.2 - Prove that abxdx=b2a22.Ch. 5.2 - Prove that abx2dx=b3a33.Ch. 5.2 - Express the integral as a limit of Riemann sums....Ch. 5.2 - Express the integral as a limit of Riemann sums....Ch. 5.2 - The graph of f is shown. Evaluate each integral by...Ch. 5.2 - The graph of g consists of two straight lines and...Ch. 5.2 - Evaluate the integral by interpreting it in terms...Ch. 5.2 - Evaluate the integral by interpreting it in terms...Ch. 5.2 - Evaluate the integral by interpreting it in terms...Ch. 5.2 - Evaluate the integral by interpreting it in terms...Ch. 5.2 - Evaluate the integral by interpreting it in terms...Ch. 5.2 - Evaluate the integral by interpreting it in terms...Ch. 5.2 - Evaluate 111+x4dx.Ch. 5.2 - Given that 0sin4xdx=83, what is 0sin4d?Ch. 5.2 - In Example 5.1.2 we showed that 01x2dx13. Use this...Ch. 5.2 - Use the properties of integrals and the result of...Ch. 5.2 - Use the result of Example 3 to evaluate 13ex+2dx.Ch. 5.2 - Prob. 46ECh. 5.2 - Write as a single integral in the form abf(x)dx:...Ch. 5.2 - If 28f(x)dx=7.3 and 24f(x)dx=5.9, find 48f(x)dx.Ch. 5.2 - If 09f(x)dx=37 and 09g(x)dx=16, find...Ch. 5.2 - Find 05f(x)dx if f(x)={3forx3xforx3Ch. 5.2 - For the function f whose graph is shown, list the...Ch. 5.2 - If , F(x)=2xf(t)dt, where f is the function whose...Ch. 5.2 - Each of the regions A, B, and C bounded by the...Ch. 5.2 - Suppose f has absolute minimum value m and...Ch. 5.2 - Use the properties of integrals to verify the...Ch. 5.2 - Use the properties of integrals to verify the...Ch. 5.2 - Use the properties of integrals to verify the...Ch. 5.2 - Use the properties of integrals to verify the...Ch. 5.2 - Use Property 8 to estimate the value of the...Ch. 5.2 - Use Property 8 to estimate the value of the...Ch. 5.2 - Use Property 8 to estimate the value of the...Ch. 5.2 - Use Property 8 to estimate the value of the...Ch. 5.2 - Use Property 8 to estimate the value of the...Ch. 5.2 - Use Property 8 to estimate the value of the...Ch. 5.2 - Use properties of integrals, together with...Ch. 5.2 - Use properties of integrals, together with...Ch. 5.2 - Which of the integrals 12arctanxdx, 12arctanxdx,...Ch. 5.2 - Which of the integrals 00.5cos(x2)dx, 00.5cosxdx...Ch. 5.2 - Prob. 69ECh. 5.2 - (a) If f is continuous on [a, b], show that...Ch. 5.2 - Let f(x) = 0 if x is any rational number and f(x)...Ch. 5.2 - Let f(0) = 0 and f(x) = 1/x if 0 x 1. Show that...Ch. 5.2 - Express the limit as a definite integral....Ch. 5.2 - Express the limit as a definite integral....Ch. 5.2 - Find 12x2dx. Hint: Choose xi to be the geometric...Ch. 5.3 - Explain exactly what is meant by the statement...Ch. 5.3 - Let g(x)=0xf(t)dt, where f is the function whose...Ch. 5.3 - Let g(x)=0xf(t)dt, where f is the function whose...Ch. 5.3 - Let g(x)=0xf(t)dt, where f is the function whose...Ch. 5.3 - Sketch the area represented by g(x). Then find...Ch. 5.3 - Sketch the area represented by g(x). Then find...Ch. 5.3 - Use Part 1 of the Fundamental Theorem of Calculus...Ch. 5.3 - Use Part 1 of the Fundamental Theorem of Calculus...Ch. 5.3 - Use Part 1 of the Fundamental Theorem of Calculus...Ch. 5.3 - Use Part 1 of the Fundamental Theorem of Calculus...Ch. 5.3 - Use Part 1 of the Fundamental Theorem of Calculus...Ch. 5.3 - Use Part 1 of the Fundamental Theorem of Calculus...Ch. 5.3 - Use Part 1 of the Fundamental Theorem of Calculus...Ch. 5.3 - Use Part 1 of the Fundamental Theorem of Calculus...Ch. 5.3 - Use Part 1 of the Fundamental Theorem of Calculus...Ch. 5.3 - Use Part 1 of the Fundamental Theorem of Calculus...Ch. 5.3 - Use Part 1 of the Fundamental Theorem of Calculus...Ch. 5.3 - Use Part 1 of the Fundamental Theorem of Calculus...Ch. 5.3 - Evaluate the integral. 13(x2+2x4)dxCh. 5.3 - Evaluate the integral. 11x100dxCh. 5.3 - Evaluate the integral. 02(45t334t2+25t)dtCh. 5.3 - Evaluate the integral. 01(18v3+16v7)dvCh. 5.3 - Evaluate the integral. 19xdxCh. 5.3 - Evaluate the integral. 18x2/3dxCh. 5.3 - Evaluate the integral. /6sindCh. 5.3 - Evaluate the integral. 55edxCh. 5.3 - Evaluate the integral. 01(u+2)(u3)duCh. 5.3 - Evaluate the integral. 04(4t)tdtCh. 5.3 - Evaluate the integral. 142+x2xdxCh. 5.3 - Evaluate the integral. 12(3u2)(u+1)duCh. 5.3 - Evaluate the integral. /6/2csctcottdtCh. 5.3 - Evaluate the integral. /4/3csc2dCh. 5.3 - Evaluate the integral. 01(1+r)3drCh. 5.3 - Evaluate the integral. 03(2sinxex)dxCh. 5.3 - Evaluate the integral. 12v3+3v6v4dvCh. 5.3 - Evaluate the integral. 1183zdzCh. 5.3 - Evaluate the integral. 01(xe+ex)dxCh. 5.3 - Evaluate the integral. 01coshtdtCh. 5.3 - Evaluate the integral. 1/3381+x2dxCh. 5.3 - Evaluate the integral. 13y32y2yy2dyCh. 5.3 - Evaluate the integral. 042sdsCh. 5.3 - Evaluate the integral. 1/21/241x2dxCh. 5.3 - Evaluate the integral....Ch. 5.3 - Evaluate the integral....Ch. 5.3 - Sketch the region enclosed by the given curves and...Ch. 5.3 - Sketch the region enclosed by the given curves and...Ch. 5.3 - Sketch the region enclosed by the given curves and...Ch. 5.3 - Sketch the region enclosed by the given curves and...Ch. 5.3 - Use a graph to give a rough estimate of the area...Ch. 5.3 - Prob. 50ECh. 5.3 - Use a graph to give a rough estimate of the area...Ch. 5.3 - Use a graph to give a rough estimate of the area...Ch. 5.3 - Evaluate the integral and interpret it as a...Ch. 5.3 - Prob. 54ECh. 5.3 - What is wrong with the equation? 21x4dx=x33]21=38Ch. 5.3 - Prob. 56ECh. 5.3 - What is wrong with the equation?...Ch. 5.3 - What is wrong with the equation? 0sec2xdx=tanx]0=0Ch. 5.3 - Find the derivative of the function....Ch. 5.3 - Find the derivative of the function....Ch. 5.3 - Find the derivative of the function. F(x)=xx2et2dtCh. 5.3 - Find the derivative of the function....Ch. 5.3 - Find the derivative of the function....Ch. 5.3 - If f(x)=0x(1t2)et2dt, on what interval is f...Ch. 5.3 - On what interval is the curve y=0xt2t2+t+2dt...Ch. 5.3 - Let F(x)=1xf(t)dt, where f is the function whose...Ch. 5.3 - Let F(x)=2xet2dt. Find an equation of the tangent...Ch. 5.3 - If f(x)=0sinx1+t2dt and g(y)=3yf(x)dx, find g(/6).Ch. 5.3 - Prob. 69ECh. 5.3 - The error function erf(x)=20xet2dt is used in...Ch. 5.3 - Let g(x)=0xf(t)dt, where f is the function whose...Ch. 5.3 - Let g(x)=0xf(t)dt, where f is the function whose...Ch. 5.3 - Evaluate the limit by first recognizing the sum as...Ch. 5.3 - Evaluate the limit by first recognizing the sum as...Ch. 5.3 - Prob. 77ECh. 5.3 - If f is continuous and g and h are differentiable...Ch. 5.3 - (a) Show that 11+x31+x3 for x 0. (b) Show that...Ch. 5.3 - (a) Show that cos(x2) cos x for 0 x 1. (b)...Ch. 5.3 - Show that 0510x2x4+x2+1dx0.1 by comparing the...Ch. 5.3 - Let f(x)={0ifx0xif0x12xif1x20ifx2 and...Ch. 5.3 - Find a function f and a number a such that...Ch. 5.3 - The area labeled B is three times the area labeled...Ch. 5.3 - A manufacturing company owns a major piece of...Ch. 5.3 - A high-tech company purchases a new computing...Ch. 5.4 - Verify by differentiation that the formula is...Ch. 5.4 - Verify by differentiation that the formula is...Ch. 5.4 - Verify by differentiation that the formula is...Ch. 5.4 - Verify by differentiation that the formula is...Ch. 5.4 - Find the general indefinite integral....Ch. 5.4 - Find the general indefinite integral. x54dxCh. 5.4 - Find the general indefinite integral....Ch. 5.4 - Find the general indefinite integral....Ch. 5.4 - Find the general indefinite integral....Ch. 5.4 - Find the general indefinite integral. t(t2+3t+2)dtCh. 5.4 - Find the general indefinite integral. 1+x+xxdxCh. 5.4 - Find the general indefinite integral....Ch. 5.4 - Find the general indefinite integral....Ch. 5.4 - Prob. 14ECh. 5.4 - Find the general indefinite integral. (2+tan2)dCh. 5.4 - Prob. 16ECh. 5.4 - Prob. 17ECh. 5.4 - Find the general indefinite integral. sin2xsinxdxCh. 5.4 - Find the general indefinite integral. Illustrate...Ch. 5.4 - Find the general indefinite integral. Illustrate...Ch. 5.4 - Evaluate the integral. 23(x23)dxCh. 5.4 - Evaluate the integral. 12(4x33x2+2x)dxCh. 5.4 - Evaluate the integral. 20(12t4+14t3t)dtCh. 5.4 - Evaluate the integral. 03(1+6w210w4)dwCh. 5.4 - Evaluate the integral. 02(2x3)(4x2+1)dxCh. 5.4 - Evaluate the integral. 11t(1t)2dtCh. 5.4 - Evaluate the integral. 0(5ex+3sinx)dxCh. 5.4 - Evaluate the integral. 12(1x24x3)dxCh. 5.4 - Evaluate the integral. 14(4+6uu)duCh. 5.4 - Evaluate the integral. 0141+p2dpCh. 5.4 - Evaluate the integral. 01x(x3+x4)dxCh. 5.4 - Prob. 32ECh. 5.4 - Evaluate the integral. 12(x22x)dxCh. 5.4 - Evaluate the integral. 01(5x5x)dxCh. 5.4 - Evaluate the integral. 01(x10+10x)dxCh. 5.4 - Evaluate the integral. 0/4sectandCh. 5.4 - Evaluate the integral. 0/41+cos2cos2dCh. 5.4 - Evaluate the integral. 0/3sin+sintan2sec2dCh. 5.4 - Evaluate the integral. 182+tt23dtCh. 5.4 - Evaluate the integral. 10102exsinhx+coshxdxCh. 5.4 - Evaluate the integral. 03/2dr1r2Ch. 5.4 - Evaluate the integral. 02(x1)3x2dxCh. 5.4 - Evaluate the integral. 01/3t21t41dtCh. 5.4 - Evaluate the integral. 022x1dxCh. 5.4 - Evaluate the integral. 12(x2x)dxCh. 5.4 - Evaluate the integral. 03/2sinxdxCh. 5.4 - Prob. 47ECh. 5.4 - Prob. 48ECh. 5.4 - The area of the region that lies to the right of...Ch. 5.4 - The boundaries of the shaded region are the...Ch. 5.4 - If w(t) is the rate of growth of a child in pounds...Ch. 5.4 - Prob. 52ECh. 5.4 - If oil leaks from a tank at a rate of r(t) gallons...Ch. 5.4 - A honeybee population starts with 100 bees and...Ch. 5.4 - In Section 4.7 we defined the marginal revenue...Ch. 5.4 - If f(x) is the slope of a trail at a distance of x...Ch. 5.4 - Prob. 57ECh. 5.4 - If the units for x are feet and the units for a(x)...Ch. 5.4 - The velocity function (in meters per second) is...Ch. 5.4 - The velocity function (in meters per second) is...Ch. 5.4 - The acceleration function (in m/s2) and the...Ch. 5.4 - The acceleration function (in m/s2) and the...Ch. 5.4 - The linear density of a rod of length 4 m is given...Ch. 5.4 - Water flows from the bottom of a storage tank at a...Ch. 5.4 - The velocity of a car was read from its...Ch. 5.4 - Suppose that a volcano is erupting and readings of...Ch. 5.4 - The marginal cost of manufacturing x yards of a...Ch. 5.4 - Prob. 68ECh. 5.4 - The graph of the acceleration a(t) of a car...Ch. 5.4 - Lake Lanier in Georgia, USA, is a reservoir...Ch. 5.4 - A bacteria population is 4000 at time t = 0 and...Ch. 5.4 - Prob. 72ECh. 5.4 - Prob. 73ECh. 5.5 - Evaluate the integral by making the given...Ch. 5.5 - Evaluate the integral by making the given...Ch. 5.5 - Evaluate the integral by making the given...Ch. 5.5 - Evaluate the integral by making the given...Ch. 5.5 - Evaluate the integral by making the given...Ch. 5.5 - Evaluate the integral by making the given...Ch. 5.5 - Evaluate the indefinite integral. x1x2dxCh. 5.5 - Evaluate the indefinite integral. x2ex3dxCh. 5.5 - Evaluate the indefinite integral. (12x)9dxCh. 5.5 - Evaluate the indefinite integral. sint1+costdtCh. 5.5 - Evaluate the indefinite integral. cos(t/2)dtCh. 5.5 - Evaluate the indefinite integral. sec22dCh. 5.5 - Evaluate the indefinite integral. dx53xCh. 5.5 - Evaluate the indefinite integral. y2(4y3)2/3dyCh. 5.5 - Evaluate the indefinite integral. cos3sindCh. 5.5 - Evaluate the indefinite integral. e5rdrCh. 5.5 - Evaluate the indefinite integral. eu(1eu)2duCh. 5.5 - Evaluate the indefinite integral. sinxxdxCh. 5.5 - Evaluate the indefinite integral. a+bx23ax+bx3dxCh. 5.5 - Evaluate the indefinite integral. z2z3+1dzCh. 5.5 - Evaluate the indefinite integral. (lnx)2xdxCh. 5.5 - Evaluate the indefinite integral. sinxsin(cosx)dxCh. 5.5 - Evaluate the indefinite integral. sec2tan3dCh. 5.5 - Evaluate the indefinite integral. xx+2dxCh. 5.5 - Evaluate the indefinite integral. ex1+exdxCh. 5.5 - Evaluate the indefinite integral. dxax+b(a0)Ch. 5.5 - Evaluate the indefinite integral. (x2+1)(x3+3x)4dxCh. 5.5 - Evaluate the indefinite integral. ecostsintdtCh. 5.5 - Evaluate the indefinite integral. 5tsin(5t)dtCh. 5.5 - Evaluate the indefinite integral. sec2xtan2xdxCh. 5.5 - Evaluate the indefinite integral. (arctanx)2x2+1dxCh. 5.5 - Evaluate the indefinite integral. xx2+4dxCh. 5.5 - Evaluate the indefinite integral. cos(1+5t)dtCh. 5.5 - Evaluate the indefinite integral. cos(/x)x2dxCh. 5.5 - Evaluate the indefinite integral. cotxcsc2xdxCh. 5.5 - Evaluate the indefinite integral. 2t2t+3dtCh. 5.5 - Evaluate the indefinite integral. sinh2xcoshxdxCh. 5.5 - Evaluate the indefinite integral. dtcos2t1+tantCh. 5.5 - Evaluate the indefinite integral. sin2x1+cos2xdxCh. 5.5 - Evaluate the indefinite integral. sinx1+cos2xdxCh. 5.5 - Evaluate the indefinite integral. cotxdxCh. 5.5 - Evaluate the indefinite integral. cos(lnt)tdtCh. 5.5 - Evaluate the indefinite integral. dx1x2sin1xCh. 5.5 - Evaluate the indefinite integral. x1+x4dxCh. 5.5 - Evaluate the indefinite integral. 1+x1+x2dxCh. 5.5 - Evaluate the indefinite integral. x22+xdxCh. 5.5 - Evaluate the indefinite integral. x(2x+5)8dxCh. 5.5 - Evaluate the indefinite integral. x3x2+1dxCh. 5.5 - Evaluate the indefinite integral. Illustrate and...Ch. 5.5 - Prob. 50ECh. 5.5 - Prob. 51ECh. 5.5 - Evaluate the indefinite integral. Illustrate and...Ch. 5.5 - Prob. 53ECh. 5.5 - Evaluate the definite integral. 01(3t1)50dtCh. 5.5 - Evaluate the definite integral. 011+7x3dxCh. 5.5 - Evaluate the definite integral. 03dx5x+1Ch. 5.5 - Evaluate the definite integral. 0/6sintcos2tdtCh. 5.5 - Evaluate the definite integral. /32/3csc2(12t)dtCh. 5.5 - Evaluate the definite integral. 12e1/xx2dxCh. 5.5 - Evaluate the definite integral. 01xex2dxCh. 5.5 - Evaluate the definite integral. /4/4(x3+x4tanx)dxCh. 5.5 - Evaluate the definite integral. 0/2cosxsin(sinx)dxCh. 5.5 - Evaluate the definite integral. 013dx(1+2x)23Ch. 5.5 - Evaluate the definite integral. 0axa2x2dxCh. 5.5 - Evaluate the definite integral. 0axx2+a2dx(a0)Ch. 5.5 - Evaluate the definite integral. /3/3x4sinxdxCh. 5.5 - Evaluate the definite integral. 12xx1dxCh. 5.5 - Evaluate the definite integral. 04x1+2xdxCh. 5.5 - Evaluate the definite integral. ee4dxxlnxCh. 5.5 - Evaluate the definite integral. 02(x1)e(x1)2dxCh. 5.5 - Evaluate the definite integral. 01ez+1ez+zdzCh. 5.5 - Prob. 72ECh. 5.5 - Evaluate the definite integral. 01dx(1+x)4Ch. 5.5 - Verify that f(x)=sinx3 is an odd function and use...Ch. 5.5 - Prob. 75ECh. 5.5 - Prob. 76ECh. 5.5 - Evaluate 22(x+3)4x2dx by writing it as a sum of...Ch. 5.5 - Evaluate 01x1x4dx by making a substitution and...Ch. 5.5 - Which of the following areas are equal? Why?Ch. 5.5 - A model for the basal metabolism rate, in kcal/h,...Ch. 5.5 - An oil storage tank ruptures at time t = 0 and oil...Ch. 5.5 - A bacteria population starts with 400 bacteria and...Ch. 5.5 - Breathing is cyclic and a full respiratory cycle...Ch. 5.5 - The rate of growth of a fish population was...Ch. 5.5 - Dialysis treatment removes urea and other waste...Ch. 5.5 - Alabama Instruments Company has set up a...Ch. 5.5 - If f is continuous and 04f(x)dx=10, find...Ch. 5.5 - If f is continuous and 09f(x)dx=4, find...Ch. 5.5 - Prob. 89ECh. 5.5 - Prob. 90ECh. 5.5 - If a and b are positive numbers, show that...Ch. 5.5 - If f is continuous on [0, ], use the substitution...Ch. 5.5 - Use Exercise 92 to evaluate the integral...Ch. 5.5 - (a) If f is continuous, prove that...Ch. 5 - (a) Write an expression for a Riemann sum of a...Ch. 5 - (a) Write the definition of the definite integral...Ch. 5 - State the Midpoint Rule.Ch. 5 - State both parts of the Fundamental Theorem of...Ch. 5 - (a) State the Net Change Theorem. (b) If r(t) is...Ch. 5 - Suppose a particle moves back and forth along a...Ch. 5 - (a) Explain the meaning of the indefinite integral...Ch. 5 - Explain exactly what is meant by the statement...Ch. 5 - State the Substitution Rule. In practice, how do...Ch. 5 - Determine whether the statement is true or false....Ch. 5 - Determine whether the statement is true or false....Ch. 5 - Determine whether the statement is true or false....Ch. 5 - Determine whether the statement is true or false....Ch. 5 - Determine whether the statement is true or false....Ch. 5 - Determine whether the statement is true or false....Ch. 5 - Determine whether the statement is true or false....Ch. 5 - Prob. 8RQCh. 5 - Prob. 9RQCh. 5 - Prob. 10RQCh. 5 - Prob. 11RQCh. 5 - Prob. 12RQCh. 5 - Prob. 13RQCh. 5 - Prob. 14RQCh. 5 - Determine whether the statement is true or false....Ch. 5 - Prob. 16RQCh. 5 - Determine whether the statement is true or false....Ch. 5 - Prob. 18RQCh. 5 - Use the given graph of f to find the Riemann sum...Ch. 5 - Prob. 2RECh. 5 - Evaluate 01(x+1x2)dx by interpreting it in terms...Ch. 5 - Express limxi=1nsinxix as a definite integral on...Ch. 5 - If 06f(x)dx=10 and 04f(x)dx=7, find 46f(x)dx.Ch. 5 - (a) Write 15(x+2x5)dx as a limit of Riemann sums,...Ch. 5 - The figure shows the graphs of f, f, and 0xf(t)dt....Ch. 5 - Evaluate: (a) 01ddx(earctanx)dx (b)...Ch. 5 - The graph of f consists of the three line segments...Ch. 5 - Prob. 10RECh. 5 - Prob. 11RECh. 5 - Prob. 12RECh. 5 - Evaluate the integral, if it exists. 01(1x9)dxCh. 5 - Evaluate the integral, if it exists. 01(1x)9dxCh. 5 - Evaluate the integral, if it exists. 19u2u2uduCh. 5 - Evaluate the integral, if it exists. 01(u4+1)2duCh. 5 - Evaluate the integral, if it exists. 01y(y2+1)5dyCh. 5 - Evaluate the integral, if it exists. 02y21+y3dyCh. 5 - Evaluate the integral, if it exists. 15dt(t4)2Ch. 5 - Prob. 20RECh. 5 - Evaluate the integral, if it exists. 01v2cos(v3)dvCh. 5 - Evaluate the integral, if it exists. 11sinx1+x2dxCh. 5 - Evaluate the integral, if it exists....Ch. 5 - Evaluate the integral, if it exists. 01ex1+e2xdxCh. 5 - Prob. 25RECh. 5 - Evaluate the integral, if it exists. 110xx24dxCh. 5 - Evaluate the integral, if it exists. x+2x2+4xdxCh. 5 - Evaluate the integral, if it exists. csc2x1+cotxdxCh. 5 - Evaluate the integral, if it exists. sintcostdtCh. 5 - Evaluate the integral, if it exists....Ch. 5 - Evaluate the integral, if it exists. exxdxCh. 5 - Evaluate the integral, if it exists. sin(lnx)xdxCh. 5 - Evaluate the integral, if it exists....Ch. 5 - Evaluate the integral, if it exists. x1x4dxCh. 5 - Evaluate the integral, if it exists. x31+x4dxCh. 5 - Evaluate the integral, if it exists. sinh(1+4x)dxCh. 5 - Evaluate the integral, if it exists. sectan1+secdCh. 5 - Evaluate the integral, if it exists....Ch. 5 - Evaluate the integral, if it exists. 03x24dxCh. 5 - Evaluate the integral, if it exists. 04x1dxCh. 5 - Evaluate the indefinite integral. Illustrate and...Ch. 5 - Evaluate the indefinite integral. Illustrate and...Ch. 5 - Prob. 43RECh. 5 - Prob. 44RECh. 5 - Prob. 45RECh. 5 - Prob. 46RECh. 5 - Prob. 47RECh. 5 - Find the derivative of the function....Ch. 5 - Prob. 49RECh. 5 - Prob. 50RECh. 5 - Prob. 51RECh. 5 - Prob. 52RECh. 5 - Use the properties of integrals to verify the...Ch. 5 - Use the properties of integrals to verify the...Ch. 5 - Prob. 55RECh. 5 - Prob. 56RECh. 5 - Use the Midpoint Rule with n = 6 to approximate...Ch. 5 - A particle moves along a line with velocity...Ch. 5 - Prob. 59RECh. 5 - A radar gun was used to record the speed of a...Ch. 5 - A population of honeybees increased at a rate of...Ch. 5 - Prob. 62RECh. 5 - Prob. 63RECh. 5 - Prob. 66RECh. 5 - Prob. 69RECh. 5 - Prob. 70RECh. 5 - Prob. 71RECh. 5 - Evaluate limn1n[(1n)9+(2n)9+(3n)9++(nn)9]Ch. 5 - Prob. 1PCh. 5 - Prob. 2PCh. 5 - If 04e(x2)4dx=k, find the value 04xe(x2)4dx.Ch. 5 - Prob. 5PCh. 5 - Prob. 6PCh. 5 - Evaluate limx0(1/x)0x(1tan2t)1/tdt. (Assume that...Ch. 5 - The figure shows two regions in the first...Ch. 5 - Find the interval [a, b] for which the value of...Ch. 5 - Use an integral to estimate the sum i=110000i.Ch. 5 - (a) Evaluate 0nxdx, where n is a positive integer....Ch. 5 - A circular disk of radius r is used in an...Ch. 5 - Prob. 15PCh. 5 - The figure shows a region consisting of all points...Ch. 5 - Evaluate limn(1nn+1+1nn+2++1nn+n).
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Recommended textbooks for you
 Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,

Elementary Geometry For College Students, 7e
Geometry
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Cengage,
Area Between The Curve Problem No 1 - Applications Of Definite Integration - Diploma Maths II; Author: Ekeeda;https://www.youtube.com/watch?v=q3ZU0GnGaxA;License: Standard YouTube License, CC-BY