
Calculus: An Applied Approach (MindTap Course List)
10th Edition
ISBN: 9781305860919
Author: Ron Larson
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Concept explainers
Question
Chapter 5.6, Problem 5E
To determine
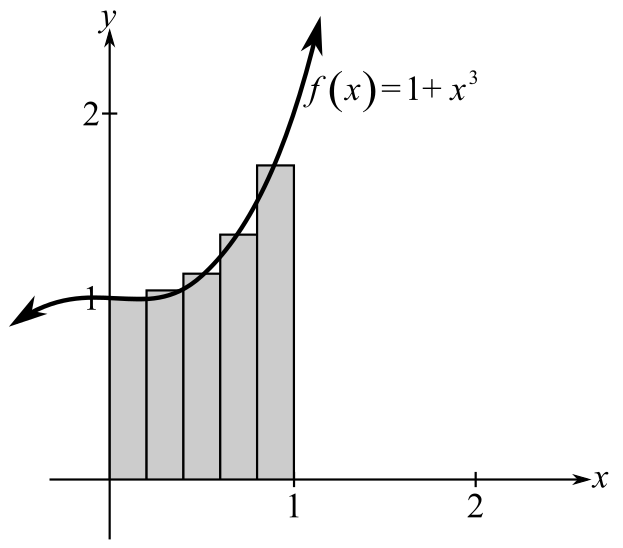
To calculate: The area bounded by the function
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Using Completing the square evaluate the integral below
evaluate the integral
the integral of e^-square root of r divided by the square root of r dr
show all work
a. Approximate the value of the integral by using rectangles. For your approximation use right endpoints and let n = 4
b. Evaluate the integral by interpreting it in terms of areas. Draw a picture
c. Evaluate the integral using the Fundamental Theorem of Calculus Part 2 FTC2)
Chapter 5 Solutions
Calculus: An Applied Approach (MindTap Course List)
Ch. 5.1 - Checkpoint 1 Worked-out solution available at...Ch. 5.1 - Prob. 2CPCh. 5.1 - Prob. 3CPCh. 5.1 - Prob. 4CPCh. 5.1 - Prob. 5CPCh. 5.1 - Prob. 6CPCh. 5.1 - Checkpoint 7 Worked-out solution available at...Ch. 5.1 - Prob. 8CPCh. 5.1 - Prob. 1SWUCh. 5.1 - Prob. 2SWU
Ch. 5.1 - Prob. 3SWUCh. 5.1 - Prob. 4SWUCh. 5.1 - Prob. 5SWUCh. 5.1 - Prob. 6SWUCh. 5.1 - In Exercises 7-10, let (x, y) = (2, 2), and solve...Ch. 5.1 - Prob. 8SWUCh. 5.1 - Prob. 9SWUCh. 5.1 - Prob. 10SWUCh. 5.1 - Integration and Differentiation In Exercises 1- 6,...Ch. 5.1 - Integration and Differentiation In Exercises 1- 6,...Ch. 5.1 - Integration and Differentiation In Exercises 1- 6,...Ch. 5.1 - Integration and Differentiation In Exercises 1- 6,...Ch. 5.1 - Integration and Differentiation In Exercises 1- 6,...Ch. 5.1 - Prob. 6ECh. 5.1 - Finding Indefinite Integrals In Exercises 7-18,...Ch. 5.1 - Prob. 8ECh. 5.1 - Finding Indefinite Integrals In Exercises 7-18,...Ch. 5.1 - Prob. 10ECh. 5.1 - Prob. 11ECh. 5.1 - Prob. 12ECh. 5.1 - Finding Indefinite Integrals In Exercises 7-18,...Ch. 5.1 - Prob. 14ECh. 5.1 - Finding Indefinite Integrals In Exercises 7-18,...Ch. 5.1 - Finding Indefinite Integrals In Exercises 7-18,...Ch. 5.1 - Finding Indefinite Integrals In Exercises 7-18,...Ch. 5.1 - Prob. 18ECh. 5.1 - Rewriting Before Integrating In Exercises 19-24,...Ch. 5.1 - Prob. 20ECh. 5.1 - Rewriting Before Integrating In Exercises 19-24,...Ch. 5.1 - Rewriting Before Integrating In Exercises 19-24,...Ch. 5.1 - Rewriting Before Integrating In Exercises 19-24,...Ch. 5.1 - Prob. 24ECh. 5.1 - Finding Indefinite Integrals In Exercises 25-36,...Ch. 5.1 - Prob. 26ECh. 5.1 - Finding indefinite integrals In Exercises 2536,...Ch. 5.1 - Prob. 28ECh. 5.1 - Finding indefinite integrals In Exercises 2536,...Ch. 5.1 - Prob. 30ECh. 5.1 - Finding indefinite integrals In Exercises 2536,...Ch. 5.1 - Prob. 32ECh. 5.1 - Finding indefinite integrals In Exercises 2536,...Ch. 5.1 - Prob. 34ECh. 5.1 - Finding indefinite integrals In Exercises 2536,...Ch. 5.1 - Prob. 36ECh. 5.1 - Using Technology In Exercises 37 and 38, use a...Ch. 5.1 - Prob. 38ECh. 5.1 - Prob. 39ECh. 5.1 - Prob. 40ECh. 5.1 - Interpreting a Graph In Exercises 3942, the graph...Ch. 5.1 - Prob. 42ECh. 5.1 - Finding a Particular Solution In Exercises 4350,...Ch. 5.1 - Prob. 44ECh. 5.1 - Finding a Particular Solution In Exercises 4350,...Ch. 5.1 - Finding a Particular Solution In Exercises 4350,...Ch. 5.1 - Prob. 47ECh. 5.1 - Prob. 48ECh. 5.1 - Finding a Particular Solution In Exercises 4350,...Ch. 5.1 - Prob. 50ECh. 5.1 - Prob. 51ECh. 5.1 - Prob. 52ECh. 5.1 - Prob. 53ECh. 5.1 - Prob. 54ECh. 5.1 - Finding a Cost Function In Exercises 5558, find...Ch. 5.1 - Prob. 56ECh. 5.1 - Finding a Cost Function In Exercises 5558, find...Ch. 5.1 - Prob. 58ECh. 5.1 - Revenue and Demand In Exercises 59 and 60, find...Ch. 5.1 - Prob. 60ECh. 5.1 - Prob. 61ECh. 5.1 - Prob. 62ECh. 5.1 - Prob. 63ECh. 5.1 - Prob. 64ECh. 5.1 - Vertical Motion In Exercises 6568, use s(t)=32...Ch. 5.1 - Prob. 66ECh. 5.1 - Prob. 67ECh. 5.1 - Prob. 68ECh. 5.1 - Prob. 69ECh. 5.1 - Gardening An evergreen nursery usually sells a...Ch. 5.1 - Population growth The growth rate of the...Ch. 5.1 - Prob. 72ECh. 5.1 - Vital Statistics The rate of increase of the...Ch. 5.1 - Prob. 74ECh. 5.1 - Economics: Marginal Benefits and Costs The table...Ch. 5.2 - Checkpoint 1 Worked-out solution available at...Ch. 5.2 - Prob. 2CPCh. 5.2 - Prob. 3CPCh. 5.2 - Prob. 4CPCh. 5.2 - Prob. 5CPCh. 5.2 - Prob. 6CPCh. 5.2 - Checkpoint 7 Worked-out solution available at...Ch. 5.2 - Prob. 8CPCh. 5.2 - Prob. 1SWUCh. 5.2 - Prob. 2SWUCh. 5.2 - Prob. 3SWUCh. 5.2 - Prob. 4SWUCh. 5.2 - Prob. 5SWUCh. 5.2 - Prob. 6SWUCh. 5.2 - Prob. 7SWUCh. 5.2 - Prob. 8SWUCh. 5.2 - Prob. 9SWUCh. 5.2 - Finding u and du/dx In Exercises 1-8, identify u...Ch. 5.2 - Finding u and du/dx In Exercises 1-8, identify u...Ch. 5.2 - Finding u and du/dx In Exercises 1-8, identify u...Ch. 5.2 - Prob. 4ECh. 5.2 - Prob. 5ECh. 5.2 - Prob. 6ECh. 5.2 - Finding u and du/dx In Exercises 1-8, identify u...Ch. 5.2 - Prob. 8ECh. 5.2 - Applying the General Power Rule In Exercises 9-34,...Ch. 5.2 - Prob. 10ECh. 5.2 - Prob. 11ECh. 5.2 - Prob. 12ECh. 5.2 - Applying the General Power Rule In Exercises 9-34,...Ch. 5.2 - Prob. 14ECh. 5.2 - Applying the General Power Rule In Exercises 9-34,...Ch. 5.2 - Prob. 16ECh. 5.2 - Prob. 17ECh. 5.2 - Prob. 18ECh. 5.2 - Applying the General Power Rule In Exercises 9-34,...Ch. 5.2 - Applying the General Power Rule In Exercises 9-34,...Ch. 5.2 - Applying the General Power Rule In Exercises 9-34,...Ch. 5.2 - Prob. 22ECh. 5.2 - Applying the General Power Rule In Exercises 9-34,...Ch. 5.2 - Applying the General Power Rule In Exercises 9-34,...Ch. 5.2 - Applying the General Power Rule In Exercises 934,...Ch. 5.2 - Prob. 26ECh. 5.2 - Applying the General Power Rule In Exercises 934,...Ch. 5.2 - Prob. 28ECh. 5.2 - Prob. 29ECh. 5.2 - Prob. 30ECh. 5.2 - Prob. 31ECh. 5.2 - Prob. 32ECh. 5.2 - Applying the General Power Rule In Exercises 934,...Ch. 5.2 - Prob. 34ECh. 5.2 - Prob. 35ECh. 5.2 - Prob. 36ECh. 5.2 - Prob. 37ECh. 5.2 - Prob. 38ECh. 5.2 - Prob. 39ECh. 5.2 - Prob. 40ECh. 5.2 - Integration by Substitution In Exercises 3542, use...Ch. 5.2 - Prob. 42ECh. 5.2 - Comparing Methods In Exercises 43-46, (a) perform...Ch. 5.2 - Prob. 44ECh. 5.2 - Prob. 45ECh. 5.2 - Comparing Methods In Exercises 43-46, (a) perform...Ch. 5.2 - Prob. 47ECh. 5.2 - Prob. 48ECh. 5.2 - Prob. 49ECh. 5.2 - Prob. 50ECh. 5.2 - Prob. 51ECh. 5.2 - Prob. 52ECh. 5.2 - Prob. 53ECh. 5.2 - Prob. 54ECh. 5.2 - Supply In Exercises 53 and 54, find the supply...Ch. 5.2 - Supply In Exercises 53 and 54, find the supply...Ch. 5.2 - Gardening An evergreen nursery usually sells a...Ch. 5.2 - HOW DO YOU SEE IT? The graph shows the rate of...Ch. 5.2 - Prob. 59ECh. 5.2 - Marginal Propensity to Consume In Exercises 59 and...Ch. 5.2 - Prob. 61ECh. 5.2 - Prob. 62ECh. 5.3 - Checkpoint 1 Worked-out solution available at...Ch. 5.3 - Checkpoint 2 Worked out solution available at...Ch. 5.3 - Prob. 3CPCh. 5.3 - Checkpoint 4 Worked-out solution available at...Ch. 5.3 - Prob. 5CPCh. 5.3 - Prob. 6CPCh. 5.3 - Prob. 7CPCh. 5.3 - Prob. 1SWUCh. 5.3 - Prob. 2SWUCh. 5.3 - Prob. 3SWUCh. 5.3 - Prob. 4SWUCh. 5.3 - Prob. 5SWUCh. 5.3 - Prob. 6SWUCh. 5.3 - Prob. 7SWUCh. 5.3 - Prob. 8SWUCh. 5.3 - Integrating an Exponential Function In Exercises...Ch. 5.3 - Prob. 2ECh. 5.3 - Integrating an Exponential Function In Exercises...Ch. 5.3 - Prob. 4ECh. 5.3 - Prob. 5ECh. 5.3 - Prob. 6ECh. 5.3 - Integrating an Exponential Function In Exercises...Ch. 5.3 - Prob. 8ECh. 5.3 - Integrating an Exponential Function In Exercises...Ch. 5.3 - Prob. 10ECh. 5.3 - Prob. 11ECh. 5.3 - Prob. 12ECh. 5.3 - Using the log Rule for integration In Exercises...Ch. 5.3 - Prob. 14ECh. 5.3 - Using the log Rule for integration In Exercises...Ch. 5.3 - Prob. 16ECh. 5.3 - Prob. 17ECh. 5.3 - Prob. 18ECh. 5.3 - Using the log Rule for integration In Exercises...Ch. 5.3 - Prob. 20ECh. 5.3 - Using the log Rule for integration In Exercises...Ch. 5.3 - Prob. 22ECh. 5.3 - Using the log Rule for integration In Exercises...Ch. 5.3 - Prob. 24ECh. 5.3 - Using the log Rule for integration In Exercises...Ch. 5.3 - Prob. 26ECh. 5.3 - Using the log Rule for integration In Exercises...Ch. 5.3 - Using the log Rule for integration In Exercises...Ch. 5.3 - Prob. 29ECh. 5.3 - Prob. 30ECh. 5.3 - Prob. 31ECh. 5.3 - Finding indefinite integrals In Exercises 3146,...Ch. 5.3 - Finding indefinite integrals In Exercises 3146,...Ch. 5.3 - Prob. 34ECh. 5.3 - Finding indefinite integrals In Exercises 3146,...Ch. 5.3 - Prob. 36ECh. 5.3 - Prob. 37ECh. 5.3 - Prob. 38ECh. 5.3 - Finding indefinite integrals In Exercises 3146,...Ch. 5.3 - Finding indefinite integrals In Exercises 3146,...Ch. 5.3 - Prob. 41ECh. 5.3 - Prob. 42ECh. 5.3 - Finding indefinite integrals In Exercises 3146,...Ch. 5.3 - Finding indefinite integrals In Exercises 3146,...Ch. 5.3 - Prob. 45ECh. 5.3 - Prob. 46ECh. 5.3 - Prob. 47ECh. 5.3 - Prob. 48ECh. 5.3 - Prob. 49ECh. 5.3 - Prob. 50ECh. 5.3 - Prob. 51ECh. 5.3 - Biology Because of an insufficient oxygen supply,...Ch. 5.3 - Demand The marginal price for the demand of a...Ch. 5.3 - Prob. 54ECh. 5.3 - Revenue The rate of change in revenue for the...Ch. 5.3 - Revenue The rate of change in revenue for DIRECTV...Ch. 5.3 - True or False In Exercises 57 and 58, determine...Ch. 5.3 - Prob. 58ECh. 5.3 - Prob. 1QYCh. 5.3 - Prob. 2QYCh. 5.3 - Prob. 3QYCh. 5.3 - Prob. 4QYCh. 5.3 - Prob. 5QYCh. 5.3 - Prob. 6QYCh. 5.3 - Prob. 7QYCh. 5.3 - Prob. 8QYCh. 5.3 - Prob. 9QYCh. 5.3 - Prob. 10QYCh. 5.3 - Prob. 11QYCh. 5.3 - Prob. 12QYCh. 5.3 - Prob. 13QYCh. 5.3 - Prob. 14QYCh. 5.3 - Prob. 15QYCh. 5.3 - Prob. 16QYCh. 5.3 - Prob. 17QYCh. 5.3 - Prob. 18QYCh. 5.3 - Prob. 19QYCh. 5.3 - Prob. 20QYCh. 5.3 - Prob. 21QYCh. 5.4 - Checkpoint 1 Worked-out solution available at...Ch. 5.4 - Prob. 2CPCh. 5.4 - Prob. 3CPCh. 5.4 - Prob. 4CPCh. 5.4 - Prob. 5CPCh. 5.4 - Prob. 6CPCh. 5.4 - Prob. 7CPCh. 5.4 - Prob. 8CPCh. 5.4 - Prob. 9CPCh. 5.4 - Prob. 1SWUCh. 5.4 - Prob. 2SWUCh. 5.4 - Prob. 3SWUCh. 5.4 - Prob. 4SWUCh. 5.4 - Prob. 5SWUCh. 5.4 - Prob. 6SWUCh. 5.4 - Prob. 7SWUCh. 5.4 - Evaluating a Definite integral using a Geometric...Ch. 5.4 - Prob. 2ECh. 5.4 - Evaluating a Definite integral using a Geometric...Ch. 5.4 - Prob. 4ECh. 5.4 - Evaluating a Definite integral using a Geometric...Ch. 5.4 - Prob. 6ECh. 5.4 - Using Properties of Definite Integrals In...Ch. 5.4 - Using Properties of Definite Integrals In...Ch. 5.4 - Finding Area by the Fundamental Theorem In...Ch. 5.4 - Finding Area by the Fundamental Theorem In...Ch. 5.4 - Finding Area by the Fundamental Theorem In...Ch. 5.4 - Prob. 12ECh. 5.4 - Finding Area by the Fundamental Theorem In...Ch. 5.4 - Prob. 14ECh. 5.4 - Finding Area by the Fundamental Theorem In...Ch. 5.4 - Prob. 16ECh. 5.4 - Evaluating a Definite Integral In Exercises 17-38,...Ch. 5.4 - Evaluating a Definite Integral In Exercises 17-38,...Ch. 5.4 - Evaluating a Definite Integral In Exercises 17-38,...Ch. 5.4 - Prob. 20ECh. 5.4 - Evaluating a Definite Integral In Exercises 17-38,...Ch. 5.4 - Prob. 22ECh. 5.4 - Prob. 23ECh. 5.4 - Prob. 24ECh. 5.4 - Evaluating a Definite Integral In Exercises 17-38,...Ch. 5.4 - Prob. 26ECh. 5.4 - Evaluating a Definite Integral In Exercises 17-38,...Ch. 5.4 - Prob. 28ECh. 5.4 - Evaluating a Definite Integral In Exercises 17-38,...Ch. 5.4 - Prob. 30ECh. 5.4 - Evaluating a Definite Integral In Exercises 17-38,...Ch. 5.4 - Evaluating a Definite Integral In Exercises 17-38,...Ch. 5.4 - Prob. 33ECh. 5.4 - Evaluating a Definite Integral In Exercises 17-38,...Ch. 5.4 - Evaluating a Definite Integral In Exercises 1738,...Ch. 5.4 - Evaluating a Definite Integral In Exercises 1738,...Ch. 5.4 - Prob. 37ECh. 5.4 - Prob. 38ECh. 5.4 - Definite Integral Involving Absolute Value In...Ch. 5.4 - Definite Integral Involving Absolute Value In...Ch. 5.4 - Definite Integral Involving Absolute Value In...Ch. 5.4 - Prob. 42ECh. 5.4 - Prob. 43ECh. 5.4 - Prob. 44ECh. 5.4 - Prob. 45ECh. 5.4 - Prob. 46ECh. 5.4 - Prob. 47ECh. 5.4 - Prob. 48ECh. 5.4 - Prob. 49ECh. 5.4 - Prob. 50ECh. 5.4 - Prob. 51ECh. 5.4 - Prob. 52ECh. 5.4 - Prob. 53ECh. 5.4 - Prob. 54ECh. 5.4 - Prob. 55ECh. 5.4 - Prob. 56ECh. 5.4 - Prob. 57ECh. 5.4 - Prob. 58ECh. 5.4 - Prob. 59ECh. 5.4 - Prob. 60ECh. 5.4 - Prob. 61ECh. 5.4 - Prob. 62ECh. 5.4 - Integrating Even and Odd Functions In Exercises...Ch. 5.4 - Prob. 64ECh. 5.4 - Using Properties of Definite Integrals Use the...Ch. 5.4 - Prob. 66ECh. 5.4 - Finding the Amount of an Annuity In Exercises...Ch. 5.4 - Prob. 68ECh. 5.4 - Finding the Amount of an Annuity In Exercises...Ch. 5.4 - Prob. 70ECh. 5.4 - Capital Accumulation In Exercises 71-74, you are...Ch. 5.4 - Prob. 72ECh. 5.4 - Prob. 73ECh. 5.4 - Capital Accumulation In Exercises 71-74, you are...Ch. 5.4 - Cost The total cost of purchasing a piece of...Ch. 5.4 - Depreciation A company purchases a new machine for...Ch. 5.4 - Prob. 77ECh. 5.4 - HOW DO YOU SEE IT? A college graduate has two job...Ch. 5.4 - Mortgage Debt The rate of change of mortgage debt...Ch. 5.5 - Checkpoint 1 Worked-out solution available at...Ch. 5.5 - Prob. 2CPCh. 5.5 - Prob. 3CPCh. 5.5 - Prob. 4CPCh. 5.5 - Prob. 5CPCh. 5.5 - Prob. 6CPCh. 5.5 - Prob. 1SWUCh. 5.5 - Prob. 2SWUCh. 5.5 - Prob. 3SWUCh. 5.5 - Prob. 4SWUCh. 5.5 - Prob. 5SWUCh. 5.5 - Prob. 6SWUCh. 5.5 - Prob. 7SWUCh. 5.5 - Prob. 8SWUCh. 5.5 - Finding the Area Bounded by Two Graphs In...Ch. 5.5 - Prob. 2ECh. 5.5 - Finding the Area Bounded by Two Graphs In...Ch. 5.5 - Prob. 4ECh. 5.5 - Finding the Area Bounded by Two Graphs In...Ch. 5.5 - Prob. 6ECh. 5.5 - Prob. 7ECh. 5.5 - Finding the Area Bounded by Two Graphs In...Ch. 5.5 - Prob. 9ECh. 5.5 - Prob. 10ECh. 5.5 - Prob. 11ECh. 5.5 - Prob. 12ECh. 5.5 - Prob. 13ECh. 5.5 - Prob. 14ECh. 5.5 - Finding the Area Bounded by Two Graphs In...Ch. 5.5 - Prob. 16ECh. 5.5 - Finding the Area Bounded by Two Graphs In...Ch. 5.5 - Prob. 18ECh. 5.5 - Prob. 19ECh. 5.5 - Prob. 20ECh. 5.5 - Prob. 21ECh. 5.5 - Prob. 22ECh. 5.5 - Finding the Area Bounded by Two Graphs In...Ch. 5.5 - Prob. 24ECh. 5.5 - Prob. 25ECh. 5.5 - Prob. 26ECh. 5.5 - Prob. 27ECh. 5.5 - Prob. 28ECh. 5.5 - Prob. 29ECh. 5.5 - Prob. 30ECh. 5.5 - Prob. 31ECh. 5.5 - Prob. 32ECh. 5.5 - Prob. 33ECh. 5.5 - Prob. 34ECh. 5.5 - Prob. 35ECh. 5.5 - Prob. 36ECh. 5.5 - Prob. 37ECh. 5.5 - Prob. 38ECh. 5.5 - Prob. 39ECh. 5.5 - Prob. 40ECh. 5.5 - Prob. 41ECh. 5.5 - Prob. 42ECh. 5.5 - Consumer and Producer Surpluses In Exercises...Ch. 5.5 - Consumer and Producer Surpluses In Exercises...Ch. 5.5 - Consumer and Producer Surpluses In Exercises...Ch. 5.5 - Consumer and Producer Surpluses In Exercises...Ch. 5.5 - Consumer and Producer Surpluses In Exercises...Ch. 5.5 - Prob. 48ECh. 5.5 - Revenue In Exercises 49 and 50, two models, R1 and...Ch. 5.5 - Revenue In Exercises 49 and 50, two models, R1 and...Ch. 5.5 - Fuel Cost The projected fuel cost C (in millions...Ch. 5.5 - Health An epidemic was spreading such that t weeks...Ch. 5.5 - Prob. 53ECh. 5.5 - HOW DO YOU SEE IT? A state legislature is debating...Ch. 5.5 - Prob. 55ECh. 5.5 - Prob. 56ECh. 5.5 - Consumer and Producer Surpluses Factory orders for...Ch. 5.5 - Consumer and Producer Surpluses Repeat Exercise 57...Ch. 5.6 - Prob. 1CPCh. 5.6 - Prob. 2CPCh. 5.6 - Prob. 3CPCh. 5.6 - Prob. 1SWUCh. 5.6 - Prob. 2SWUCh. 5.6 - Prob. 3SWUCh. 5.6 - Prob. 4SWUCh. 5.6 - Prob. 5SWUCh. 5.6 - Prob. 6SWUCh. 5.6 - Prob. 7SWUCh. 5.6 - Prob. 8SWUCh. 5.6 - Prob. 9SWUCh. 5.6 - Prob. 10SWUCh. 5.6 - Approximating the Area of a Plane Region In...Ch. 5.6 - Prob. 2ECh. 5.6 - Prob. 3ECh. 5.6 - Prob. 4ECh. 5.6 - Prob. 5ECh. 5.6 - Approximating the Area of a Plane Region In...Ch. 5.6 - Prob. 7ECh. 5.6 - Prob. 8ECh. 5.6 - Prob. 9ECh. 5.6 - Prob. 10ECh. 5.6 - Prob. 11ECh. 5.6 - Prob. 12ECh. 5.6 - Prob. 13ECh. 5.6 - Prob. 14ECh. 5.6 - Prob. 15ECh. 5.6 - Prob. 16ECh. 5.6 - Prob. 17ECh. 5.6 - Prob. 18ECh. 5.6 - Prob. 19ECh. 5.6 - Prob. 20ECh. 5.6 - Surface Area Use the Midpoint Rule to estimate the...Ch. 5.6 - Surface Area Use the Midpoint Rule to estimate the...Ch. 5.6 - Prob. 31ECh. 5.6 - Prob. 33ECh. 5 - Finding Indefinite Integrals In Exercises 114,...Ch. 5 - Prob. 2RECh. 5 - Prob. 3RECh. 5 - Prob. 4RECh. 5 - Prob. 5RECh. 5 - Prob. 6RECh. 5 - Finding Indefinite Integrals In Exercises 114,...Ch. 5 - Prob. 8RECh. 5 - Prob. 9RECh. 5 - Prob. 10RECh. 5 - Prob. 11RECh. 5 - Prob. 12RECh. 5 - Prob. 13RECh. 5 - Finding Indefinite Integrals In Exercises 114,...Ch. 5 - Prob. 15RECh. 5 - Prob. 16RECh. 5 - Prob. 17RECh. 5 - Prob. 18RECh. 5 - Prob. 19RECh. 5 - Revenue A company produces a new product for which...Ch. 5 - Prob. 21RECh. 5 - Prob. 22RECh. 5 - Prob. 23RECh. 5 - Prob. 24RECh. 5 - Prob. 25RECh. 5 - Prob. 26RECh. 5 - Prob. 27RECh. 5 - Prob. 28RECh. 5 - Prob. 29RECh. 5 - Prob. 30RECh. 5 - Prob. 31RECh. 5 - Prob. 32RECh. 5 - Production The rate of change of the output of a...Ch. 5 - Prob. 34RECh. 5 - Prob. 35RECh. 5 - Prob. 36RECh. 5 - Prob. 37RECh. 5 - Prob. 38RECh. 5 - Prob. 39RECh. 5 - Prob. 40RECh. 5 - Prob. 41RECh. 5 - Prob. 42RECh. 5 - Prob. 43RECh. 5 - Prob. 44RECh. 5 - Prob. 45RECh. 5 - Prob. 46RECh. 5 - Prob. 47RECh. 5 - Prob. 48RECh. 5 - Prob. 49RECh. 5 - Prob. 50RECh. 5 - Prob. 51RECh. 5 - Prob. 52RECh. 5 - Prob. 53RECh. 5 - Prob. 54RECh. 5 - Prob. 55RECh. 5 - Prob. 56RECh. 5 - Prob. 57RECh. 5 - Prob. 58RECh. 5 - Prob. 59RECh. 5 - Prob. 60RECh. 5 - Evaluating a Definite Integral In Exercises 5970,...Ch. 5 - Prob. 62RECh. 5 - Prob. 63RECh. 5 - Prob. 64RECh. 5 - Prob. 65RECh. 5 - Prob. 66RECh. 5 - Prob. 67RECh. 5 - Prob. 68RECh. 5 - Prob. 69RECh. 5 - Prob. 70RECh. 5 - Prob. 71RECh. 5 - Prob. 72RECh. 5 - Prob. 73RECh. 5 - Prob. 74RECh. 5 - Prob. 75RECh. 5 - Prob. 76RECh. 5 - Prob. 77RECh. 5 - Prob. 78RECh. 5 - Prob. 79RECh. 5 - Prob. 80RECh. 5 - Prob. 81RECh. 5 - Prob. 82RECh. 5 - Prob. 83RECh. 5 - Prob. 84RECh. 5 - Prob. 85RECh. 5 - Prob. 86RECh. 5 - Prob. 87RECh. 5 - Prob. 88RECh. 5 - Prob. 89RECh. 5 - Prob. 90RECh. 5 - Prob. 91RECh. 5 - Prob. 92RECh. 5 - Prob. 93RECh. 5 - Prob. 94RECh. 5 - Prob. 95RECh. 5 - Consumer and Producer Surpluses In Exercises...Ch. 5 - Prob. 97RECh. 5 - Prob. 98RECh. 5 - Prob. 99RECh. 5 - Prob. 100RECh. 5 - Prob. 101RECh. 5 - Prob. 102RECh. 5 - Prob. 103RECh. 5 - Approximating the Area of a Plane Region In...Ch. 5 - Prob. 105RECh. 5 - Prob. 106RECh. 5 - Prob. 107RECh. 5 - Prob. 108RECh. 5 - Prob. 109RECh. 5 - Prob. 110RECh. 5 - Prob. 111RECh. 5 - Prob. 112RECh. 5 - Prob. 113RECh. 5 - Prob. 114RECh. 5 - Surface Area Use the Midpoint Rule to estimate the...Ch. 5 - Prob. 1TYSCh. 5 - Prob. 2TYSCh. 5 - Prob. 3TYSCh. 5 - Take this test as you would take a test in class....Ch. 5 - Prob. 5TYSCh. 5 - Prob. 6TYSCh. 5 - Prob. 7TYSCh. 5 - Prob. 8TYSCh. 5 - Prob. 9TYSCh. 5 - Prob. 10TYSCh. 5 - Prob. 11TYSCh. 5 - Prob. 12TYSCh. 5 - Prob. 13TYSCh. 5 - Prob. 14TYSCh. 5 - Prob. 15TYSCh. 5 - Prob. 16TYSCh. 5 - Prob. 17TYSCh. 5 - Prob. 18TYSCh. 5 - Prob. 19TYSCh. 5 - Prob. 20TYSCh. 5 - Prob. 21TYSCh. 5 - Prob. 22TYS
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- Computer giving into girl. Show the algebra necessary to convert the integral into a form where you may use one of your integration formulas.arrow_forwardIntegral Calculus, Plane Areaarrow_forwardSHOW FULL SOLUTION AND EXPLAIN. INTEGRAL CALCULUS. 1. Find the area bounded by y=lnx, x=e^2 and the x-axis, using a horizontal element.arrow_forward
- Using the fundamental theorem, find the area under the curve y = 4x3 −2x+5 and above x-axis on the interval [0,2]arrow_forwardHow do you define and calculate the area of the surface swept out by revolving the graph of a smooth function y = ƒ(x), a<=x<= b, about the x-axis? Give an examplearrow_forwardCalculus Find the area under a curve define by the equation 5x^(4)+3x+7 between the x values 0 and 4 .arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning

Calculus: Early Transcendentals
Calculus
ISBN:9781285741550
Author:James Stewart
Publisher:Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:9780134438986
Author:Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:9780134763644
Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:9781319050740
Author:Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:W. H. Freeman


Calculus: Early Transcendental Functions
Calculus
ISBN:9781337552516
Author:Ron Larson, Bruce H. Edwards
Publisher:Cengage Learning
Definite Integral Calculus Examples, Integration - Basic Introduction, Practice Problems; Author: The Organic Chemistry Tutor;https://www.youtube.com/watch?v=rCWOdfQ3cwQ;License: Standard YouTube License, CC-BY