
(a)
To show: The volume of a segment of a sphere
(a)
Answer to Problem 3P
The volume of the segment of a sphere is
Explanation of Solution
Given information:
The segment of a sphere with radius r and height h.
Consider that the Equation of circle as
Rearrange Equation (1).
The dimensions of the sphere as shown in Figure 1.
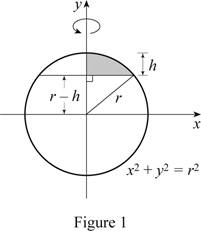
Refer to Figure 1.
Consider that the sphere is obtained by rotating the circle
The region lies between
Calculation:
The expression to find the volume of the segment of a sphere as shown below:
Find the area of the segment of a sphere as shown below.
Substitute
Therefore, the volume of the segment of a sphere is
(b)
To calculate: The value of x using Newton’s method.
(b)
Answer to Problem 3P
The value of x by using Newton’s method is 0.2235.
Explanation of Solution
Given information:
A sphere of radius 1 is sliced by a plane at a distance x from the center.
The volume of one segment is twice the volume of the other.
The Answer of the equation
Calculation:
Find the volume of the sphere as shown below.
Substitute 1 for r in Equation (3).
Consider the smaller segment has height
Refer to part (a).
Volume of the segment of a sphere as shown below:
Substitute 1 for r and
This volume must be
Substitute
Apply Newton’s method as shown below.
Consider
Differentiate both sides of the Equation.
Substitute
Consider
Substitute 1 for n in Equation (6).
Substitute 2 for n in Equation (6).
Substitute 2 for n in Equation (6).
Therefore, the value of x by using Newton’s method is 0.2235.
(c)
To calculate: sinking depth of the sphere.
(c)
Answer to Problem 3P
The sinking depth of the sphere is 0.6736 m.
Explanation of Solution
Given information:
Wooden sphere of radius as 0.5 m.
Specific gravity of the wooden sphere is 0.75.
The depth x to which a floating sphere of radius r sinks in water is a root of the equation as follows:
Calculation:
Show the root of the equation as shown below.
Substitute 0.5 m for r and 0.75 for s in Equation (7).
Consider
Differentiate both sides of the Equation.
Apply Newton’s method.
Substitute
Consider
Substitute 1 for n in Equation (8).
Substitute 2 for n in Equation (8).
Substitute 3 for n in Equation (8).
Approximately the depth should be
Therefore, the sinking depth of the sphere is 0.6736 m.
(d) i)
To calculate: The speed of rising the water level in the bowl from instant of water level at 3 inches deep.
(d) i)
Answer to Problem 3P
The speed of rising the water level in the bowl from instant of water level at 3 inches deep is
Explanation of Solution
Given information:
The shape of the bowl is hemisphere.
The radius of hemispherical bowl is 5 inches.
Water is running into the bowl at the rate of
Depth of water is 3 inches.
Calculation:
Show the volume of the segment of a sphere as follows:
Differentiate both sides of the Equation with respect to time t.
Find the speed of the water level in the bowl rising at the instant as shown below.
Substitute 5 inches for r,
Therefore, the speed of rising the water level in the bowl from instant of water level at 3 inches deep is
ii)
To calculate: The time taken to fill the bowl from 4 inch level of water.
ii)
Answer to Problem 3P
The time taken to fill the bowl from 4 inch level of water is
Explanation of Solution
Given information:
The radius of hemispherical bowl is 5 inches.
Water is running into the bowl at the rate of
Depth of water is 4 inches.
Calculation:
Find the volume of the water required to fill the bowl from the instant that the water is 4 in. depth as follows:
Substitute 5 inches for r and 4 inches for h in the Equation.
Find the time required to fill the bowl as shown below.
Therefore, The time taken to fill the bowl from 4 inch level of water is
Chapter 6 Solutions
Single Variable Calculus: Concepts and Contexts, Enhanced Edition
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





