Chapter 6.3, Problem 38E

a)

To determine

To find: the more wood content of the ring from two rings.

Answer to Problem 38E

The both napkin rings are having a same quantity of wood.

Explanation of Solution

The volume only depends up on the height of the napkin ring.

Hence, the both napkin rings are having same quantity of wood.

b)

To determine

To check: The part (a) answer by computing the volume of a napkin ring using cylindrical shells.

Answer to Problem 38E

The volume of a napkin ring is $\underset{\_}{\frac{\pi h^3}{6}}$

Explanation of Solution

Given:

The height of the napkin ring is h.

The radius of the napkin ring is r.

The radius of the sphere is R.

Calculation:

Consider the equation of napkin ring as follows:

$y=\sqrt{R^2-x^2}$ (1)

The region lies between $x=r$ and $x=R$.

Sketch the solid region as shown below in Figure 1.

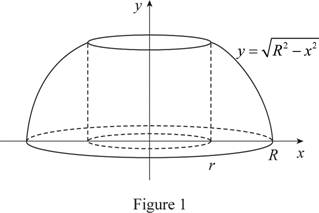
Refer Figure 1

Calculate the volume using the method of cylindrical shell as follows.

$V=2\times {\displaystyle {\int }_a^{b}2\pi x\left[f\left(x\right)\right]dx}$ (2)

Substitute r for a, R for b, and $\sqrt{R^2-x^2}$ for $\left[f\left(x\right)\right]$ in equation (2).

$\begin{array}{c}V=2{\displaystyle {\int }_r^{R}2\pi x\sqrt{R^2-x^2}dx}\\ =2\pi {\displaystyle {\int }_r^{R}2x\sqrt{R^2-x^2}dx}\end{array}$ (3)

Consider $u=R^2-x^2$ (4)

Differentiate both sides of the equation.

$\begin{array}{c}du=-2xdx\\ -du=2xdx\end{array}$

Calculate the lower limit value of u using equation (4).

Substitute r for x in equation (4).

$u=R^2-r^2$

Calculate the upper limit value of u using equation (4).

Substitute R for x in equation (4).

$\begin{array}{c}u=R^2-R^2\\ =0\end{array}$

Apply lower and upper limits for u in equation (3).

Substitute u for $\left(R^2-x^2\right)$ and $\left(-du\right)$ for $2xdx$ dx in equation (3).

$\begin{array}{c}V=2\pi {\displaystyle {\int }_{R^2+r^2}^0\sqrt{u}\left(-du\right)}\\ =-2\pi {\displaystyle {\int }_{R^2+r^2}^0{u}^{\frac{1}{2}}du}\end{array}$ (5)

Integrate equation (5).

$\begin{array}{c}V=-2\pi {\left[\frac{u^{\frac{1}{2}+1}}{\frac{1}{2}+1}\right]}_{R^2+r^2}^0\\ =-2\pi {\left[\frac{u^{\frac{3}{2}}}{\frac{3}{2}}\right]}_{R^2+r^2}^0\\ =-2\pi \left[\frac{2{\left(0\right)}^{\frac{3}{2}}}{3}-\frac{2{\left(R^2+r^2\right)}^{\frac{3}{2}}}{3}\right]\\ =\frac{4}{3}\pi {\left(R^2+r^2\right)}^{\frac{3}{2}}\end{array}$ (6)

Consider $R^2+r^2={\left(\frac{h}{2}\right)}^2$

Substitute ${\left(\frac{h}{2}\right)}^2$ for $R^2+r^2$ in equation (6).

$\begin{array}{c}V=\frac{4}{3}\pi {\left(\frac{h}{2}\right)}^{2\times \frac{3}{2}}\\ =\frac{4}{24}\pi h^3\\ =\frac{1}{6}\pi h^3\end{array}$

Hence, the volume of a napkin ring is $\underset{\_}{\frac{\pi h^3}{6}}$.